微分積分とは?高校数学の基礎から応用までわかりやすい記事総まとめ

微分・積分とは?数学Ⅲ関連記事総まとめ

このページでは、主に数学Ⅲの微分・積分と微分法・積分法の応用（問題の解き方）について解説した記事をまとめています。（数学２で習う範囲であっても、重要なものは合わせて掲載しています）

（※：2020/03/15更新。内容がかなり増えてきているので、ブックマーク！推奨です）

数学Ⅲの微積分は、数学２での微分積分よりも複雑な関数を計算し、問題のレベルもアップします。

しかし、本質的には数２の微積分と考え方は変わりません。

また、出題されるパターンもある程度決まっているので、理系・医系で合格点を取っている人はこの分野を得点源にしています。

(「数３をこれから学ぶ主に高校生向けのおススメ勉強法&復習記事」を作成しました。)

現在進行形で記事を作成しているので、さらに追加していきます。

↓タップ・クリックして知りたい記事へ飛べる目次↓

微分とは？そして微分法の応用のまとめ

基本的な微分公式は全て抑えておきましょう。

微分とは？基本的な微分公式・計算法

※以下の微分公式は「微分法の定義と様々な微分」の記事で詳しく解説しています。

証明は、微分法の定義(導関数の求め方)と三角関数などの諸公式から行う事ができます。

微分の定義

そもそも微分・導関数はどのような式で定義されているのか、その基礎です。

連鎖律・乗法公式・商公式・線形性

特に数学Ⅲでの微分でよく使う、「積の微分・商の微分・連鎖律(合成関数微分)」などの簡単なまとめです。

三角関数・指数・対数関数の微分

整式の微分(基本)

本格的に微分に入る前に、極限分野は大丈夫ですか？

極限分野のまとめ

極限分野は微分積分の基礎であるだけでなく、微分法や積分法の応用といった分野でパワーアップして顔を出します。(例：「区分求積法」積分法の項で紹介しています）

数Ⅲは「極限に始まって極限に終わる」と言われるくらい、実は非常に大切な分野です。

「極限分野を得点源にする為の記事6選まとめ」

微分係数と導関数の違いと意味（数2・数３共通）

「定義に従って導関数を求めよ」という問題や、導関数と微分係数の違いがよくわからないなら、この記事を読んでみてください。

「”微分係数”と”導関数”の意味と違いを徹底解説！」

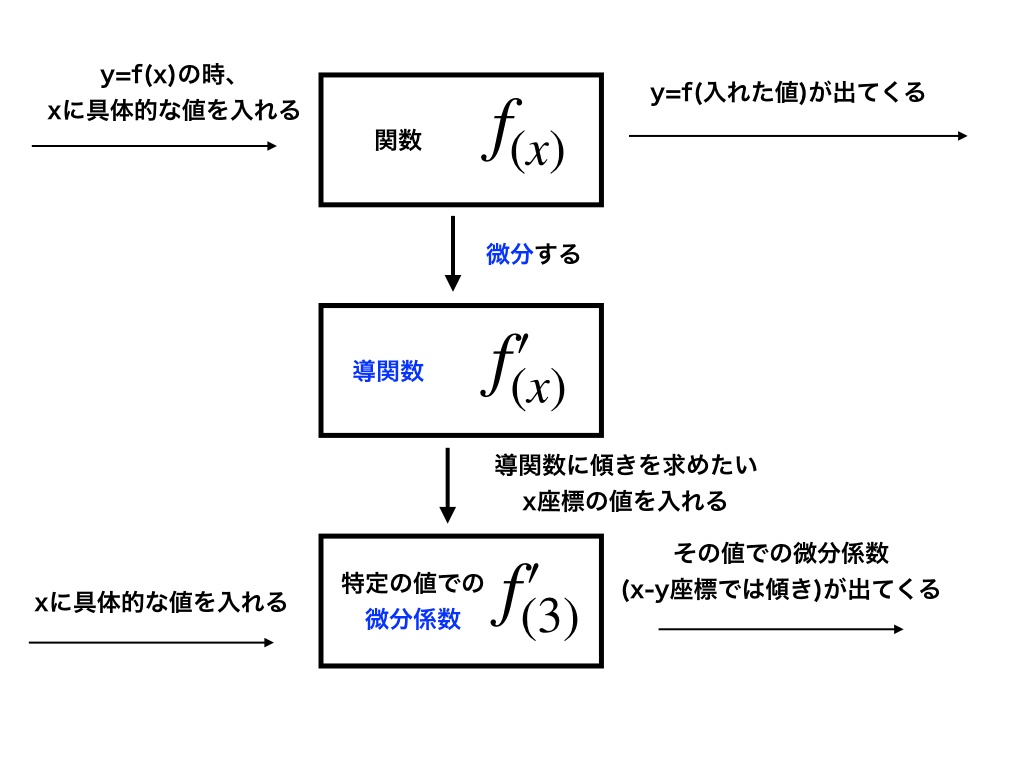
＜上のような内容を解説しています＞

三次関数の微分とグラフ・極値（数学２）

数学３の微分法に不安があれば、先に数２の微分を復習しておきましょう！

「数学２：三次関数のグラフの描き方・増減表・極値の求め方と応用問題の解き方」

微分法(数学Ⅲ)のキソ

数IIの微分よりも対象となる関数が増え、微分の方法も増える数学Ⅲの微分それぞれを詳しく解説しました。

「関数の連続と微分可能の違いとは？」では、次の『微分の定義』と共によく理解しておく必要がある”連続”と”微分可能”の相違点について紹介しています。

微分の定義とさまざまな関数の微分

これまで、xの式の微分だけを扱っていましたが、数3では他にも「三角関数や、指数・対数関数」を微分したり、

そのままでは微分しにくい関数を色々な工夫（対数微分法・合成関数の微分等）をして解いていきます。

以下の3記事は数Ⅲの基礎体力になる部分です。必ず身に付ける様にしましょう。

「微分法の定義と様々な関数の微分」

対数微分法や合成関数・陰関数微分のやり方

例えば、f(x)=x^{x}といった関数などを微分する際には、これまでの方法では歯が立ちません。

「陰関数と陰関数微分が分かる！」

「合成関数の微分と対数微分法が分かる！」

上の二つの微分法をなるべく早くマスターして置くことが重要です。

微分法の応用問題の解き方

ここでは、数学Ⅲの微分法を使って、接線と法線を求めたり平均値の定理・不等式の証明などの問題を扱います。

グラフを作成する手順（非常に重要です）

微分法を習うとグラフを書いたり、のちに出てくる面積や体積を求める際に、すぐに増減表を作る（書く）癖がついてきます。

もちろん増減表も大切なのですが、あえて最初から増減表を作らずにグラフの概形を捉える重要さとメリット、そして方法を「グラフを描く時増減表を作成してはいけない理由とは」で解説しています。

接線・法線の式の求め方

その名の通り接線・法線の求め方です。ここで→「接線と法線の方程式の求め方（数Ⅲ）」対象とする関数のグラフがこれまでの２次・3次の多項式の関数から、様々な関数に変わります。

（積分との融合）接線とグラフ・軸で囲まれた部分の面積・体積

上の記事の応用versionです。

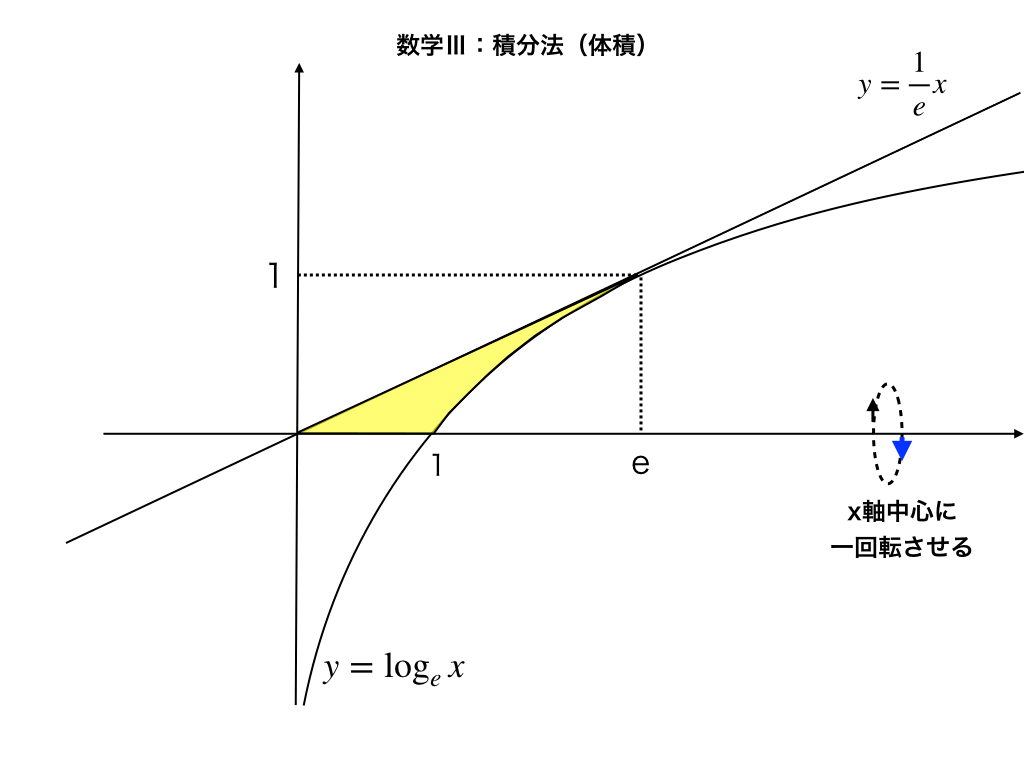
積分法との融合問題として、「接線とグラフなどが囲む面積＋体積」は超頻出です。ぜひチェックしておきましょう。

平均値の定理と応用

あいまいな理解になりがちな「平均値の定理」を、「平均値の定理とは？その意味と不等式の証明への応用」←のページでイラストを用いてわかりやすく解説しています。

ニュートン法の仕組みと問題の解き方

難関大・学部で頻出のニュートン法。目的やその仕組みがよく分からない人のために「ニュートン法をわかりやすく！近似値の求まる仕組み〜例題の解き方まで」で実例を挙げて紹介しました。

特に”近似値が求める仕組み”は一発で理解できるよう工夫して図を作成しました。

偏微分とは(応用)

高校範囲外ですが、知っておくと多変数関数の問題や、包絡線(数２：図形と方程式の『軌跡』の分野)を求める時に役立つ【偏微分と全微分】の”基礎”を紹介しています。

「偏微分と全微分の仕方とイメージ」

＜応用なので、難しく感じる人は飛ばして構いません＞

積分と積分法の応用記事まとめ

さて、微分と対になる積分（数Ⅲver）に入って行きます。

・数ⅱの積分とは計算量も難易度も格段に上がる点

・さらに積分法の応用（面積・体積・弧長・微分方程式etc,,,）からの出題のウェイトが非常に大きいため、

早いうちから基本を押さえておく必要があります。

積分法(数学Ⅲ)のキソ・計算

積分法（数３）の基本的な公式などを紹介しています。

「積分法の基礎を一から学ぶ」

偶関数と奇関数（数２・数３共通）

偶関数と奇関数について、「偶関数と奇関数とは？種類・見分け方・応用法まで解説！」で詳しく紹介しています。

1/6公式とその応用のコツ

「1/6公式と関連する公式の紹介と『実践的な工夫』のコツ」を作成しました。

上にある『偶関数・奇関数』の記事と合わせて利用すれば、さらにspeed up &ミスを減らすことが可能になります。

部分積分の仕方(と微分する関数の選び方)

ここでは、部分積分法の仕方を詳しく解説しています。

この記事→「部分積分法とは？その解き方とコツ」では、なるべくイラストを多く利用して部分積分の手順をわかりやすく解説しました。

また、部分積分でよくある『どの関数を”微分”して、どの関数を”積分”するのか分からない！』という悩みの解決法も具体例とともに紹介しました。

置換積分のやり方と知っておくべき置き換え

部分積分や一般的な積分の公式でも積分できない場合には、積分をする関数の一部を別の文字に置き換えて（＝置換積分）を行うことで解決することがあります。

ただし、置換積分には『積分区間の変更』や『知らないと思いつかない変換（＝特に重要です）』など、注意すべき点が多くあるので、「置換積分法とは？そのやり方と注意点・知識を解説」で詳しく紹介しました。

区分求積法

何かと記号が多く、敬遠しがちな『区分求積法』。

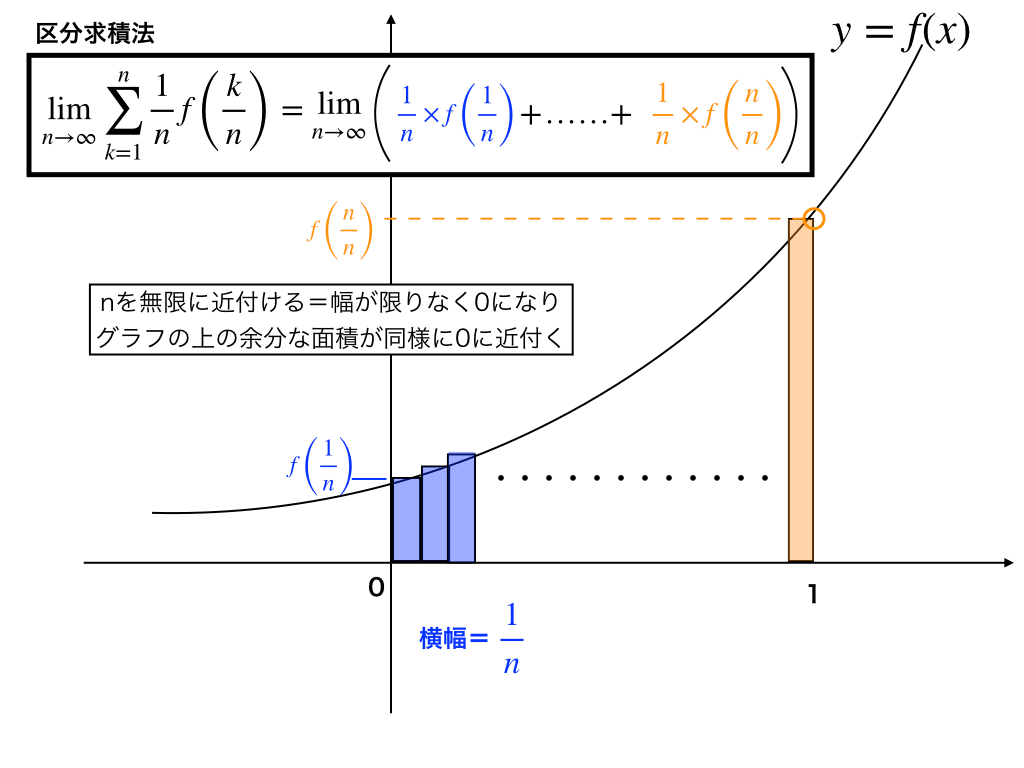
上のような↑イラストを用いて「区分求積法の式を分かりやすく！問題の解き方のコツも紹介！」の記事で０から解説しました。

積分方程式の解き方

積分方程式は、方程式の中に”∫dx”の”積分の形”が入ったもので、関数方程式（式に関数が入った方程式）の一種です。（のちに紹介する『微分方程式』もその一つです）

解法は決まっているので「積分方程式はたった2種類の解法で解ける」の記事で即マスターしてしまいましょう！

積分法の応用(数Ⅲ)問題の解き方

積分法の応用では、面積・体積・曲線の長さを求める他、極限との融合問題など難易度が高く抽象的な問題が出題されます。

ただし、冒頭でも書いた通りある程度パターンが決まっているので、この単元の習熟度で合否が決まることも珍しくありません。

積分計算でよく使う部分分数分解

予備知識として、積分の際によく使用する部分分数分解を確認しておきましょう。

「部分分数分解の仕方と応用」

積分・不等式・二項定理との融合問題

この記事→「積分法の不等式を二項定理で解く方法」は、積分の極限値を”二項定理を使ってうまく不等式で挟み込み、はさみうちの原理で求める”という難易度は高いですが、色々な分野の復習になる問題とその解説です。

積分で面積が求まる理由

「積分で面積が求まる理由をはさみうちの原理で解説」

積分漸化式の問題の解き方

積分と数列の漸化式が融合したような分野を「積分漸化式４パターンの意味と問題の解き方」で解説しました。（数列については、このページの最後にまとめを作ってあります。）

ベータ関数

「β関数とは？そして1/6公式への応用」

・・・作成中です・・・

面積・体積・曲線の長さの求め方シリーズ

数三の積分法の応用の中でも、出題率が非常に高い”面積・体積・”＋αとして『弧長』”の求め方を以下の記事でまとめています。

様々な求積法

「求積パターンまとめとx軸回転体の求積」

減衰曲線y=e-xsinx

いわゆる『減衰曲線』とそのグラフがx軸との間に囲む面積の求め方を「減衰曲線の求積パターンとグラフ」で紹介しています。

パラメーター表示された曲線

いわゆる”媒介変数”表示されている曲線の「増減表」・「グラフの描き方」・「面積」について、「媒介変数で表示された曲線の描き方・面積の求め方」で詳しく解説しました。

y軸回転体＋”バウムクーヘン”積分

x軸に関してではなく、y軸に関して一回転する物体の体積について、「”y軸”回転体の体積と”バウムクーヘン”（分割）積分」で紹介しました。

弧長（曲線の長さ）の求め方

面積・体積とくると最後に待ち構えているのは「曲線の長さ」です。以下の記事ではグラフの曲線（弧長とも言います）の求め方をまとめています。

「弧長の求め方２パターンを解説」

微分方程式の応用記事

積分法の応用の最後に「微分方程式」の記事をまとめておきます。

以下の記事では最も基本的な“変数分離型”の微分方程式の解き方と、物理や化学との融合問題を解説しました。

入試や模試ではあまり触れられることの少ない微分方程式ですが、最難関大（京大）などで出題される事があります。

また、入試対策だけでなく微分方程式の基本だけでも抑えておくと、物理や化学の現象がよりはっきり理解する事ができます。

余裕があれば、ぜひ取り組んで見てほしい分野です。

「微分方程式の解法と物理・化学への応用記事まとめ」

微積と融合した問題が作られる分野

数学Ⅲでは、これまでの高校数学の知識をフルに利用する必要があります。

特に関係の深い単元のまとめ記事へのリンクです。

数列の漸化式の解き方

数列は積分と融合して”積分漸化式”（2019/12/14：作成済みです。積分法の応用のところをご覧ください）の問題に発展したり、極限＋積分＋数列の３分野融合問題が良く出題されます。

その中でも漸化式の解き方は基礎中の基礎なので、必ず身に付けておきましょう！

「数列の漸化式の解き方11選まとめ」

二項定理とその周辺

二項定理も積分法の応用や、極限などと融合した問題でよく使います。

「二項定理とは？その公式と応用」

場合の数と確率のまとめページ

「場合の数と確率を得意分野にするための解法解説総まとめ」

(応用:社会人向け)機械学習のための数学

「機械学習に必要な数学・統計学」ではここで紹介している微積分以外にも、様々な分野・レベルの記事をまとめています。

ここまで、高校(理系)数学において最重要の微積分について、若干の応用分野を含めて解説してきました。

数学３ではこれらの解法を知っていることは当然として、計算力(ミスや速度)、抽象的な内容を把握して既知の解法に落とし込む、ある程度のアバウトさ(グラフの書き方参照)など複合的な能力が問われます。

大変な分野ですが、得意になると最も安定しやすい範囲なので、是非頑張って習得していきましょう。