関数の連続と微分可能
今回は、タイトル通り関数の連続と微分可能性について扱って行きます。
どっちがどっちだったか分からなくなったり、必要条件・十分条件で悩んでいる人に向けてこのまぎらわしい2つを解説していきます。
目次(タップした所へ飛びます)
関数の連続と微分可能の関係
・関数の種類と包含関係
・連続な関数
・微分可能な関数
・連続な関数と微分可能な関数の必要/十分条件
・連続⇒微分可能の反例
・まとめ
数学3に於いて極限と微分法の間のような分野で、非常に大事なところなのですが、イマイチ理解できない人が多い、だから出題された時に差がつく分野です。
関数の種類と包含関係
今までひとくくりに「関数」という言葉を使ってきましたが、
連続している関数や、微分可能な関数、連続していない関数など色々あります。
条件の厳しいところから並べると
微分可能な関数<連続な関数<関数;の順番に種類が増えて行きます。
したがって微分可能であれば連続な関数ですし、連続な関数であれば関数です。
当然微分可能な関数であれば、関数です。
この関係は数学1で学んだ集合の包含関係を頭に浮かべると理解しやすいと思います。
一番広いU=を全ての関数として、連続な関数を連、微分可能な関数を微と表してベン図を書くと<図1>のようになります。
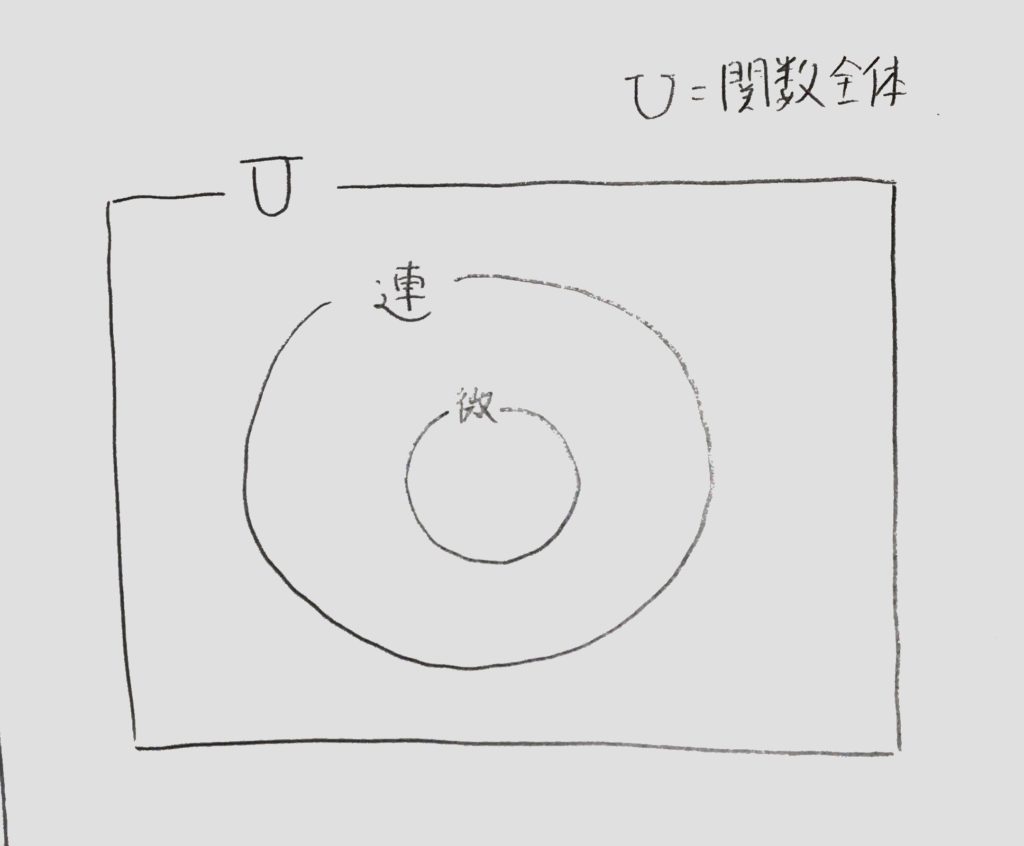
<図1:微分可能・連続な関数のベン図>
連続な関数とは
さて、では連続な関数から解説を始めます。
「連続」のイミ;ある値x=αに於いて関数f(x)が連続というのは、
右側極限=左側極限=f(α)が成立することを言います。
<参考:「極限の意味と片側極限」>
つまり<図2>のようにガウス記号が含まれている関数や、
飛び飛びの値を取る関数でなければ連続であると言えます。
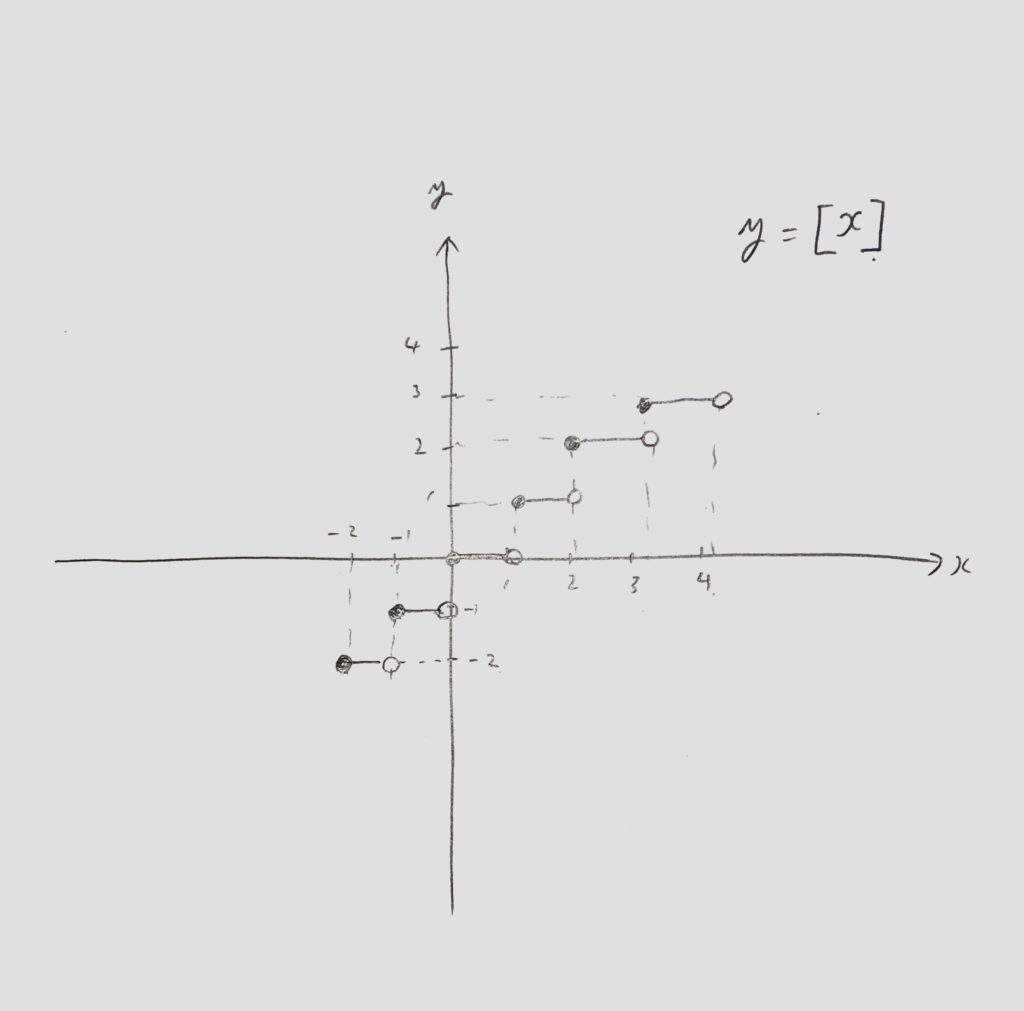
<図2:ガウス記号付きの関数のグラフy=[x]>
\(\lim _{x→ α+0}f(x) =\lim _{x→ α-0}f(x)=f(α) \)
一方で微分可能な関数は<図1>を見てもわかりますが、連続よりも更にきびしい条件があります。
微分可能な関数
微分可能な関数の条件は「連続、かつ、なめらか」である必要があります。
この「なめらか」とは一点で尖っていたり<図3>、x軸に垂直な点があったり(傾きが∞になってしまう)、その点だけ値が無い、といった状態でない場合をいいます。
<参考:「絶対値の意味と場合分け・グラフの描き方」>
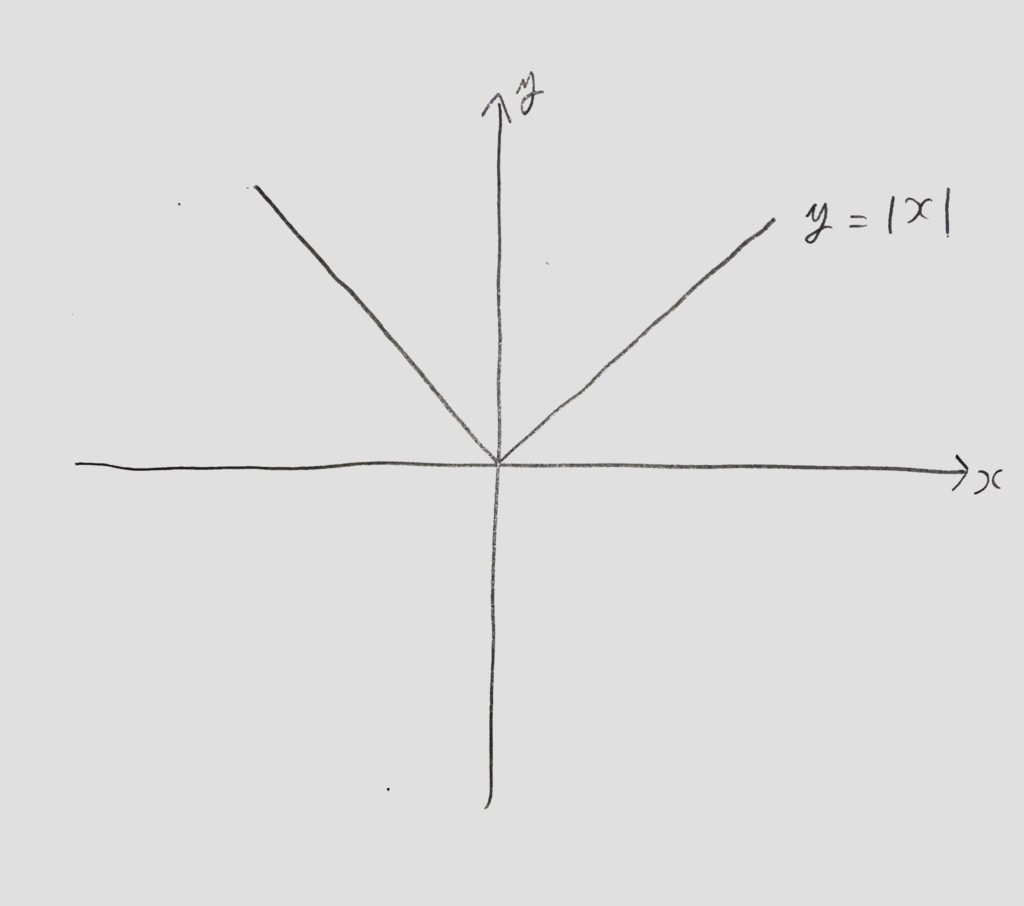
<図3:なめらかでない関数のグラフ(y=|x|)>
x=αで微分可能な関数の定義を式で書くと、それは
\(\lim _{h\rightarrow a+0}\frac {f(a+h)-f(a)}{h}=\lim _{h\rightarrow a-0}\frac {f(a+h) -f(a)}{h}\)
が成り立つことであり、右からの微分係数と、左からの微分係数が等しいことであるといえます。
<関連記事:「微分係数と導関数の違いを答えられますか?」>
連続な関数と、微分可能な関数の必要/十分条件
<参考記事:「必要条件・十分条件を判別するコツ『十要』とは?」>
ここはよく聞かれます。例えば
(1)「連続ならば微分可能なのか?」
(2)「微分可能な関数ならば連続なのか?」
というものですが、先ほどの<図1のベン図>を見て貰うと分かるように、
(関数>連続な関数>微分可能)な関数の包含関係にあるので、
微分可能⇒連続 は真ですが、 連続⇒微分可能 は偽 となります。
従って、微分可能な関数は必ず連続だが、連続な関数だからと言って微分可能とは限らない。
(1)は×、(2)は○ が正解です。
(1)「連続な関数⇒微分可能」の反例
実際に(1)が偽である反例を示しておきます。
f(x)=|x| のx=0の時を考えてみます。
まずはじめに連続である事を示しておきます。
\(\lim _{x→ +0}|x| =\lim _{x→ -0}|x| =f(0) =0\)
よって連続。
次に右側極限を調べます:
\(\lim _{h→ +0}\frac {f( 0+h)-f( 0) }{h}=\lim _{h→ +0}\frac {h}{h}=1\)
更に左側極限は、
\(\lim _{h→ -0}\frac {f(0+h)-f(0)}{h}=\lim _{h→ -0}\frac {-h}{h}=-1\)
従って、右側極限と左側極限が一致しないので極限値が存在せず、微分不可能。
連続と微分可能な関数まとめ
関数f(x)が、x=aに於いて
・連続な関数とは、左右極限とf(a)が一致するもの
・微分可能な関数とは、左右の微分係数が一致するもの
・微分可能⇒連続 は真 だが 連続⇒微分可能 は偽
今回も最後まで読んで頂きまして有難うございます。お問い合わせその他はコメント欄までお願いします。
次の記事:「数学Ⅲ微分法の定義と基本公式」を読む。

