微分係数と導関数の定義・求め方とは
微分係数や導関数の定義の式・・・公式だけ覚えて定義の意味をスルーしていませんか?
また、導関数と微分係数の違いを説明できますか。
「導関数を定義に従って求めよ」という問題が苦手なら、ぜひじっくりと読んでみてください。
目次(タップした所へ飛びます)
微分係数と導関数の違いと定義
まずはじめに大切なことは、関数の意味を理解することです
関数は工場 ?
なんとなく使っているf(x)という関数の表記ですが、「関数とは一体どのようなものか」考えた事があるでしょうか。
fはfunctionのfです。以下の図のように、関数とはx(任意の数字)をfに入れると対応した数字を出してくれる「機能:(英;function)」を持ったものです。
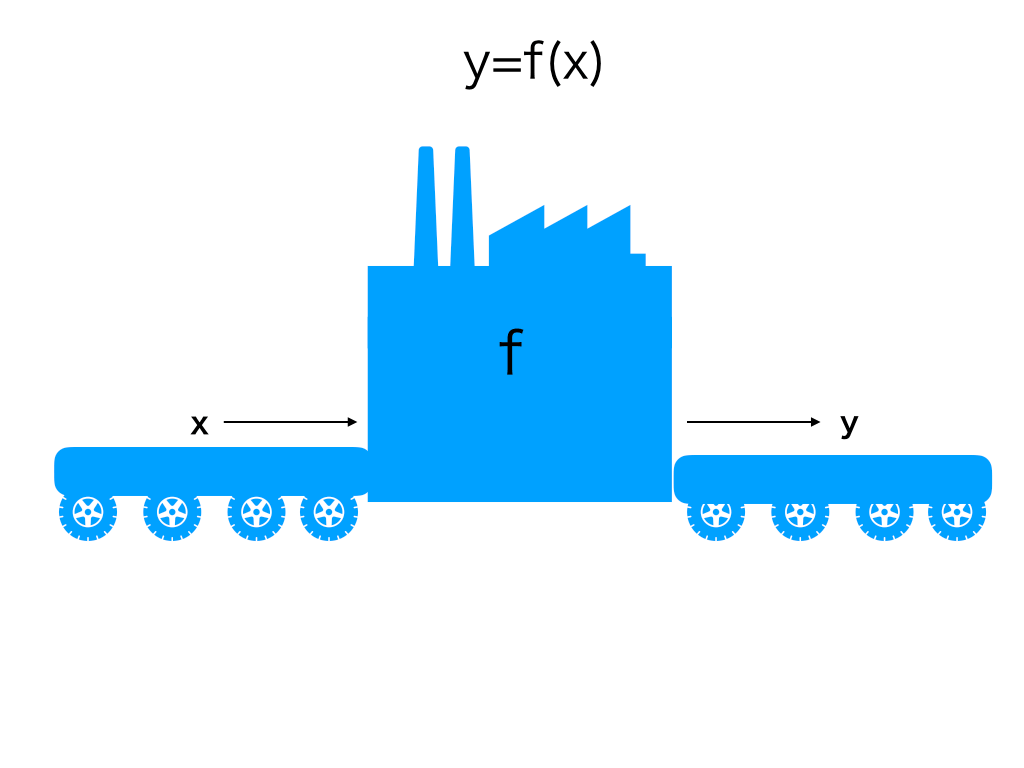
y=f(x)であれば、xを入れると対応したyという数字が出てくるわけです。(さらに詳しくは→「集合と写像;全射・単射・全単射」)
では本題の、『微分係数』と『導関数』の違いを見ていきましょう。↓今後の流れ。
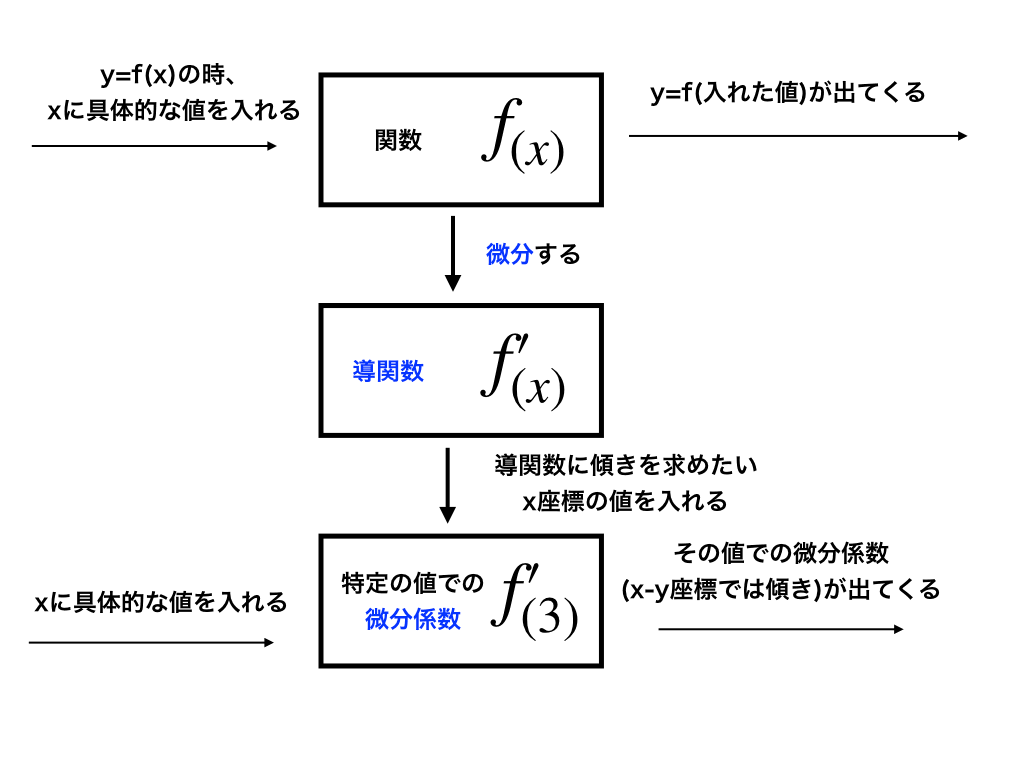
<関数→導関数→微分係数の流れ>
微分係数はある点での傾き:定数
まず、微分係数の定義の式を見て見ましょう。
$$f'(α) =\lim _{x\rightarrow α }\frac {f(x)-f(α) }{x-α}$$
\(\lim _{x\rightarrow α }\)この極限の意味は、「xを限りなくαという点に近付ける」ということです。
続いて$$\frac {f(x) -f(α) }{x-α}$$の意味は、xy座標上の2点(x、f(x))と(α、f(α))
うち、分母にx座標の差、分子にy座標の差を持ってきています。
これは「傾き」の定義の式そのままです。
そして、このxをαに限りなく近付ける「極限」によって、関数のグラフy=f(x)上のx=αでの傾きと限りなく一致することになります。
まとめると、「微分係数の定義の式」は、関数f(x)のx=α【ここでは定数という意味でαを使いました。当然、x=2ならばf(2)、x=eならばf(e)】
での「傾き」を求める操作を表していると言えます。
導”関数”は任意の場所での傾き
では、混同しがちな「導関数」とは一体なんなのでしょうか。
導関数の定義の式は以下のように表され、「導関数を求めること」=「微分すること」と習ったかと思います。
定義の式
$$f'( x) =\lim _{h\rightarrow 0}\frac {f( x+h) -f( x) }{h}$$
\(\lim _{h\rightarrow 0}\)この極限の意味はもう大丈夫かと思いますが、hを限りなく0に近付ける極限の操作のことです。
一方、微分係数の式とよく似ている$$\frac {f(x+h) -f(x) }{h}$$
をもう少しわかりやすく変形して見ます。
$$\frac {f(x+h) -f(x) }{(x+h)-(x) }$$
分母に注目です。$$( x+h) -( x) =h$$
α+hの代わりにx+hに変化しています。要するに、αという特定の数をxという変数に置き換えています。
つまり、導関数f'(x)は微分係数と違って入れる「x」の値によって変化します。
一旦導関数を求めれば、微分係数は簡単に求まる
この導関数:f'(x)は上記の通り関数なので、「x」に好きな値を入れることでその場所の傾き:微分係数が求まります。
だから『関数』と呼ぶのです。(上の「関数とは」のイメージ参照)
少しややこしいですね。。実際に定義を使って導関数を求めながら上の意味を考えていきましょう。
(このあたりの定義や式は難しく見えますし、公式だけ覚えていれば大体の問題が解けてしまうのでスルーしがちです。
ですが、これから以下で説明する関数の微分の際には必須ですし、意味を理解していないと解けない問題も出てくるので
ぜひゆっくりでいいので身につけておきましょう。)
定義に従って導関数を求めてみる
では、数2・数3分野で登場する主な関数の導関数を定義に従って自分で導いてみましょう!
グッと理解が深まるはずです。
分子にあるf(x+h)の扱い方
定義に従って〜の中で最も分かりにくいのが、このf(x+h)だと思うので実例をもとに説明していきます。
例えば、sinxの導関数を求めるときに、
$$f'( x) =\lim _{h\rightarrow 0}\frac {f(x+h) -f( x) }{h}$$
の分子のf(x+h)のところを sin(x+h)にします。
$$e^{x}の時は、同様にe^{x+h}にする$$、
つまり、元の関数の“x”の部分に(x+h)を代入して計算するイメージです。詳しくは以下で解説します。
xの整式の微分(導関数を求める)
数学2の微分で習うxのべき乗(n乗)の中でも最もシンプルな、【xの2乗】を定義に従って微分(導関数を求めて)みましょう。
・<参考記事:「【数学2】三次関数の微分とグラフ・増減表・極値の求め方【微分】」>
\(f(x)=x^{2}\)
$$f’(x)=\lim _{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$
上のコツで書きましたが、f(x +h)の(x+h)を二乗します。
$$f’(x)=\lim _{h\rightarrow 0}\frac{(x+h)^{2}-(x^{2})}{h}$$
分数部分を展開していくと、
$$分数=\frac{x^{2}+2hx+h^{2}-x^{2}}{h}$$
$$ここで\lim _{h\rightarrow 0}\frac{h^{2}}{h}=0$$
$$\lim _{h\rightarrow 0}\frac{2hx}{h}=2x$$
より、
f’(x)=2x
となります。これは微分の公式通りになっていますね。
今回は2乗で計算していますが、当然分数乗などでもこの方法で導関数を求めることができます。
三角関数の微分
今度は、三角関数の導関数を定義に従って求めてみましょう。
三角関数の予備知識
前提として、いくつかの公式を知っている必要があります(式変形で使うため)。
分からない公式があれば、「三角関数の公式の覚え方・導き方まとめ」を参照して下さい!
三角関数の極限の予備知識
主に三角関数の導関数を定義に従って求めるときには、「加法定理」と三角関数の極限の公式を使って式変形を進めます。
ここでは、最小限の極限公式を紹介しておきます。
$$\lim _{x\rightarrow 0}\frac {\sin x}{x}=1$$
$$\lim _{x\rightarrow 0}\frac {1-\cos x}{x^{2}}=\frac {1}{2}$$
sinの微分
f(x)=sinx
定義に従って導関数を求める。
$$f‘(x)=\lim _{h\rightarrow 0}\frac{\sin(x+h)- \sin(x)}{h}$$
ここで、加法定理より
\(\sin(x+h)=\sin x\cos h+\cos x\sin h\)
だから、$$\lim _{h\rightarrow 0}\frac {\sin x\cos h+\cos x\sin h-\sin x}{h}$$
三角関数の極限公式:$$\lim _{x\rightarrow 0}\frac {1-\cos x}{x^{2}}=\frac {1}{2}$$
を使うために、"-sinx"でくくり
\(\lim _{h\rightarrow 0}\left( \frac {-\sin x\left( 1-\cos h \right) }{h}+\cos x\cdot \frac {\sin h }{h}\right) \)
分母分子にhをかけて
$$\frac {1-\cos h}{h}\cdot \frac {h}{h}=h\cdot \frac {1-\cos h }{h^{2}}$$
の形にすると、$$ \frac {1-\cos h }{h^{2}}この部分が\frac {1}{2}$$
に収束し、hが0に収束するので
$$結局\lim _{h\rightarrow 0}h\cdot \frac {1-\cos h}{h^{2}}は0$$、$$よって\frac {-\sin x\left( 1-\cos h \right) }{h}$$
が0になるので、あとは$$\lim _{x\rightarrow 0}\frac {\sin x}{x}=1$$を利用して、
$$f'\left( x\right) =\cos x$$
と、導くことができました。
残りのcos、tanの導関数も同様に求めることができるのでぜひチャレンジしてみてください!
指数・対数関数の微分
最後に、指数関数・対数関数の導関数を定義に従って求めていきます。
指数・対数関数の予備知識
対数については→「常用対数とその応用」、e(自然対数の底・ネイピア数)については→「ネイピア数って何?」をご覧下さい!
指数・対数の極限の予備知識
$$\lim _{x\rightarrow 0}\frac {e^{x}-1}{x}=1$$
$$\lim _{x\rightarrow 0}\left( 1+x\right) ^{\frac {1}{x}}=e$$
指数(ex)の微分
\(f(x)=e^{x}\)
$$f’(x)=\lim _{h\rightarrow 0}\frac {f\left( x+h\right) -f\left( x\right) }{h}$$
$$\lim _{h\rightarrow 0}\frac {e^{\left( x+h\right) }-e^{x}}{h}$$
\(e^{x}\)でくくって
$$\lim _{h\rightarrow 0}\frac {e^{x}\left( e^{h}-1\right) }{h}$$
自然対数の底の極限公式:$$\lim _{x\rightarrow 0}\frac {e^{x}-1}{x}=1$$
より、$$f'( x) =\lim _{h\rightarrow 0}\frac {\left( e^{h}-1\right) }{h}e^{x}$$
$$よって、f'( x) =e^{x}$$
このようにネイピア数には微分しても(導関数を求めても)同じ形になるという特徴があります。
対数の微分
対数の真数条件(参考:「常用対数の記事」)より、x>0
\(f(x)=log_{e}x\)
$$f’(x)=\lim _{h→ 0}\frac {f(x+h)-f(x) }{h}$$
$$\lim _{h→ 0}\frac {\log \left(x+h\right)-\log x}{h}$$
対数どうしの引き算は真数の割り算なので、
$$(分子)=\log \frac{x+h}{x}=\log \left(1+\frac {h}{x}\right)$$分母を
$$\log \left(1+\frac {h}{x}\right)$$の前に出して、
\(\lim _{h\rightarrow 0}\frac {1}{h}\left(\log \left(1+\frac {h}{x}\right) \right)\)
ここで、対数の極限公式$$\lim _{x→ 0}( 1+x)^{\frac {1}{x}}=e$$
を利用するために、少し工夫します。
今、上の極限公式のxに当たるものが\(\frac {h}{x}\)なので、その逆数乗、つまり
$$\log ( 1+\frac {h}{x})^{\frac {x}{h}}の形$$
ができるように式変形を行います。
真数の肩に乗っている“べき乗”の部分はlogの前に出せるので、帳尻を合わせるために、
$$\frac {1}{h}\log ( 1+\frac {h}{x})$$
$$=\frac {1}{x}\log ( 1+\frac {h}{x})^{\frac {x}{h}}$$
このように変形します。
あとは、\(\lim _{x\rightarrow 0}の時、\)
$$ (1+\frac {h}{x})^{\frac {x}{h}}はeに収束するので、$$普通に計算を進めると、
$$f'( x) =\frac {1}{x}\log _{e}e$$
$$\log_{e}e=1だから、f'(x) =\frac {1}{x}$$
よって、公式通り$$f‘(x)=\frac{1}{x}$$を導くことができました。
まとめと微分/極限の関連記事へ
最後の対数関数の微分は少し難しかったかと思いますが、まずは「定義に従って導関数を求める、という『流れ』」(はじめに載せておいた、《関数→導関数→微分係数》の流れ」のイラストを再度確認して見てください)を理解してもらえれば
あとは類題をといているうちに必ず慣れてきます。何度か流し読みで構わないので、この記事を読み直してぜひマスターしてください!
(2019/11/25現在この記事の続編を製作中です)
今回も最後までご覧いただき、まことに有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNSでの反応などをもとに、日々改善・記事の追加および更新を行なっています。
そこで
・記事リクエストと質問・ご意見はコメント欄にお寄せください。可能な限り対応します。
・また、多くの学生・受験生に利用して頂くために、SNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為に、是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等は、お問い合わせページよりお願い致します。