求積問題(数三)の基礎から解説
＜この記事の内容と対象＞：初めて積分を用いて体積を求める方法を習う/習ったが苦手な人〜基本的な求積問題を復習したい人。
＜あわせて読む＞：「数Ⅲの微分・積分を０から発展まで解説！まとめページ」
目次(タップした所へ飛びます)
積分で体積を求める仕組みと式
数学Ⅲの積分法を応用して、体積を求めていきます。
まずは、求積問題のパターンを紹介します。（各々のパターンの詳細な解説記事を随時追加していきます。）
求積問題のパターン【理解編】
では、具体的にどの様なものの体積を計算するのか、ひとつずつ見ていきましょう。
x軸を中心にした回転体
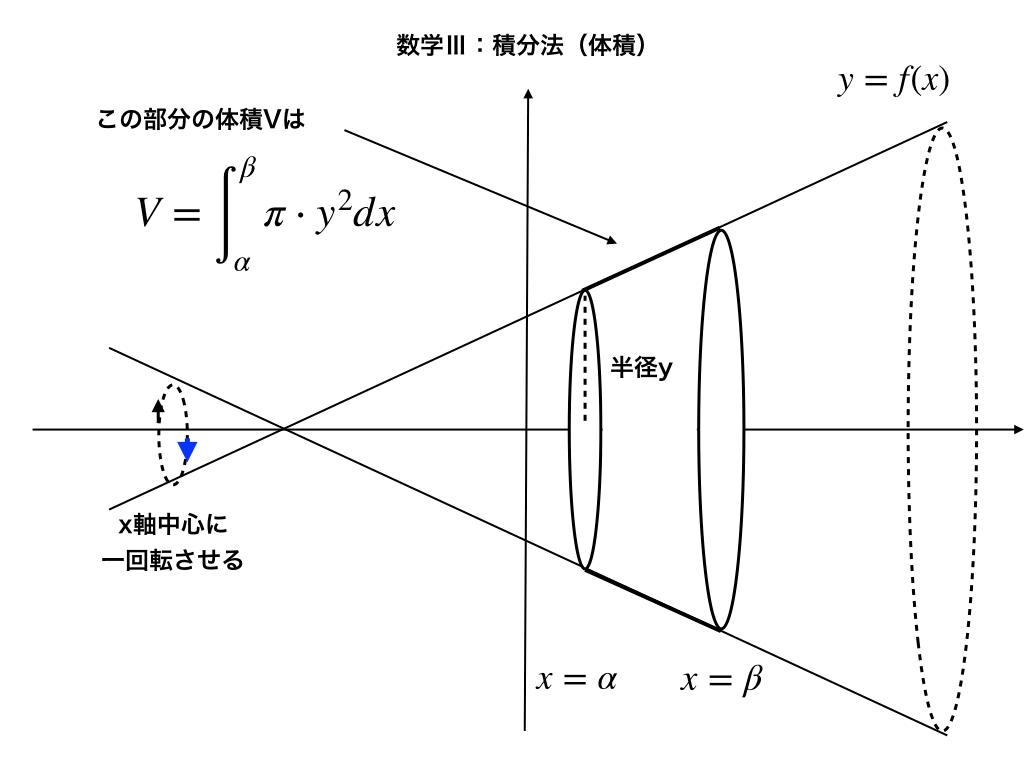
最も基本的なパターンは、この”x軸中心”の回転体の体積を求めるものです。
詳しくは下の【実践編】で解説しますが、$$V＝\pi\cdot\int^{\beta}_{\alpha}y^{2}dx$$で求まります。
半径yで高さ(ここでは微小なx)の円柱を、β→αまで積み重ねるイメージです。
y軸を中心とする回転体
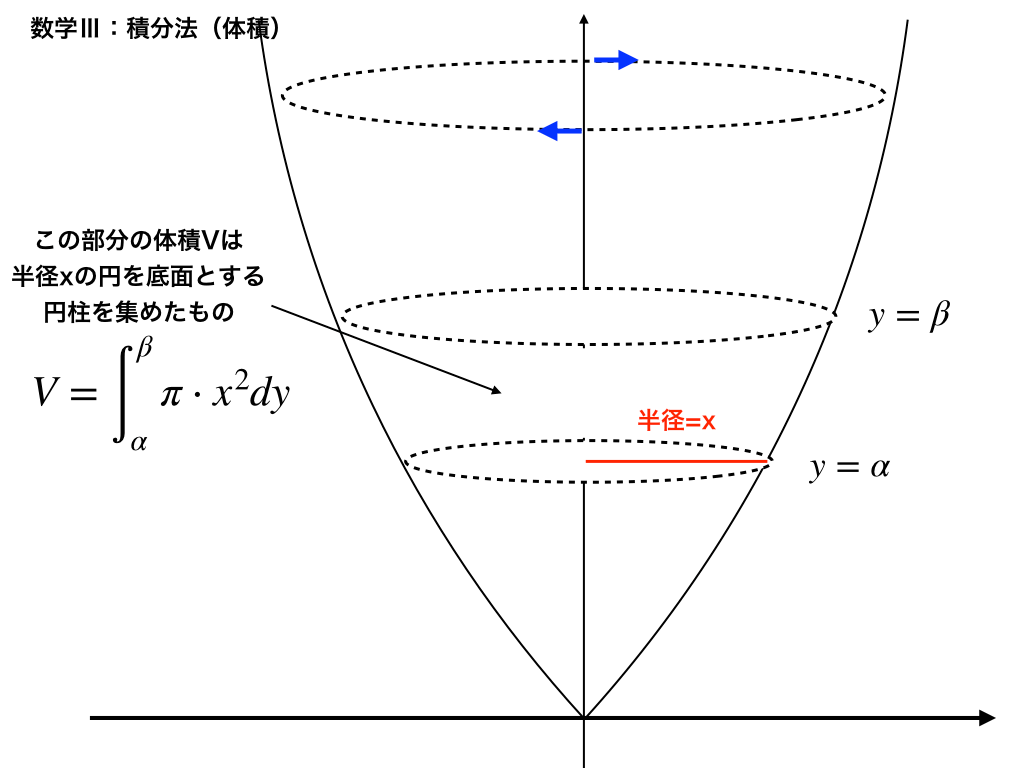
次に多いパターンが、回転軸をxからyに変えたものです。
・微小体積（半径\(x^{2}\)で高さが微小)を積分していく一般的な解き方のほかに、
・いわゆる『バームクーヘン分割（or年輪法)』という解法を利用する場合もあります。
$$V＝\int^{\beta}_{\alpha}x^{2}dy$$
y＝xなどナナメの軸を中心とする回転体
ここまでの２つは、x軸、or、y軸の周りの求積だったのでまだ理解しやすいかと思います。
が、たまにy=x（つまり原点から45°方向）を軸としてその回転体の体積を求めさせる問題が出ることがあります。
この場合には、式変形・もしくは傘型に分割して求積するテクニックを用います。
空間中の回転体
”x-y-z”座標空間内にある図形を、z軸（もしくはx ,y軸など）について回転させた時の体積を求める問題がこれにあたります。
体積を求める空間図形がどのような形になるか？を想像するのは大抵の場合困難です。
そのため、ベクトルなどの道具を用いて断面とその面積を計算し、それを積分して答えを求めます。
”パラメータ”で表示された図形とその回転体の体積
これは、「”媒介変数”によって表されたグラフ」を、さらに回転（主にx軸・y軸中心に）させたものです。
媒介変数がからんだ問題は、そもそもグラフを書くだけでも大変なことが多い上に、それを回転させるので計算量が膨大になりやすいです。
非回転体の求積
最後に、もともと図形が何らかの条件（不等式で表された領域など）で与えられているものの体積を求める問題です。
参考者などに必ずと言っていいほど出てくるもので、どの『切り口』で積分を進めるかによって、
・後の計算量や
・ミスの可能性が大きく変わるため、
しっかりと初めに方針を立てて進める(ある程度は問題をこなす)ことが大切です。
x軸中心の求積問題【実践編】
上述した様に、今回は『x軸中心』の回転体を題材にして実際に体積を求めていきます。
例題(一)
＜例題１＞：【0≦x≦π】において、\(y=\sin x とy＝0\)で囲まれた部分を、x軸を中心として一回転させた。
この時できる回転体の体積をもとめよ。
解答と解説(一)
＜解説＞：まず問題の内容を把握しましょう。
すると、以下の様なグラフの回転体の体積を求めればいいことがわかります。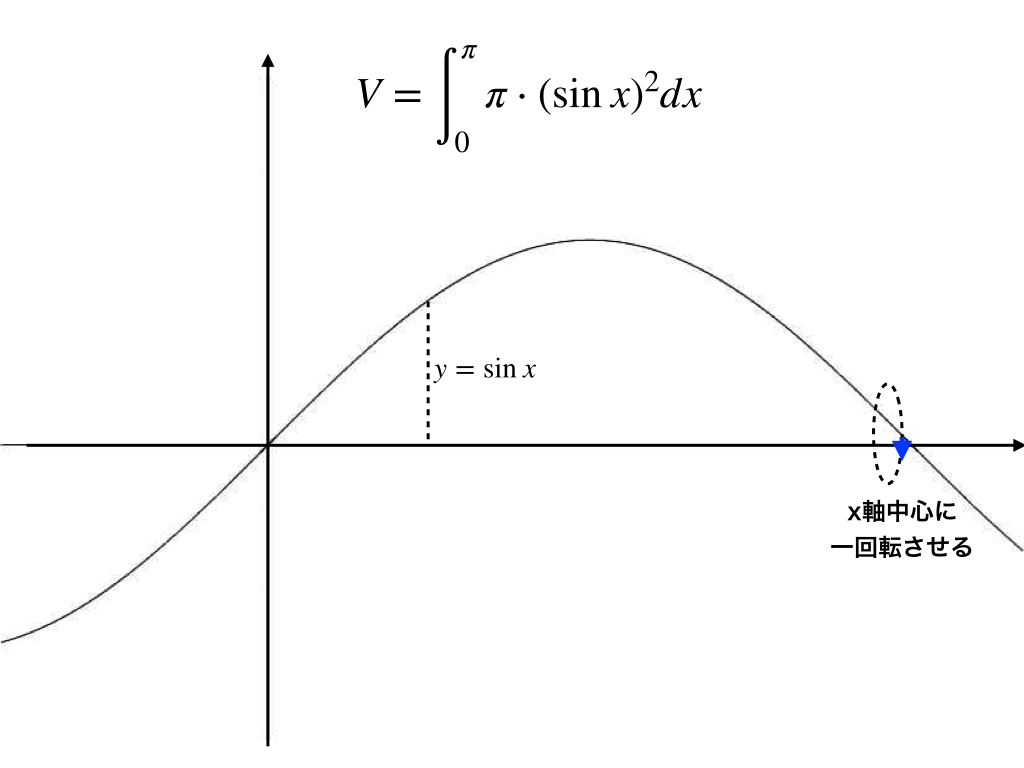
そして、上の図中にもある様に、\(半径y＝\sin x\)の円を底面とする【微小な円柱】を『０からπまで集める＝積分する』ことで問題の体積が求まります。
したがって、\(\int^{\pi}_{0}\pi\sin^{2}x dx\)を計算すれば良いので、「半角の公式(積分において三角関数の公式は超重要です！)」より、$$\sin^{2}x＝\frac{1-\cos 2x}{2}$$
$$\pi\int^{\pi}_{0}\frac{1-\cos 2x}{2} dx=\frac{\pi^{2}}{2}$$
まとめと続編(y軸回転)へ
今回は、体積を求めるシリーズの（１）として大体のパターン分けを前半で行い、最も単純なx軸についての回転体を後半の実践例題で扱いました。
次回はy軸についてのパターン(2種類)に進みます。
数学Ⅲ：微積分の記事総まとめ他
＞＞（まとめ）「基礎から応用・発展レベルまで数学３の微積分の解法・解説記事まとめ！」＜＜
数学Ⅲ体積(一)：「(今ここです)様々な求積問題のまとめと"x軸"回転体」
数学Ⅲ体積(二)：「y軸回転体の求積問題の解法”2”種類」
スマホで学ぶ、受験・学習メディア『スマナビング！』へのお問い合わせ/ご依頼に付きましては、【運営元ページ】にて、受け付けております。