
偶関数と奇関数+積分の問題で実践
<この記事の内容と読んで欲しい人>:いまいち”偶”関数や”奇”関数がよくわからない。。という人へ向けて、その意味から実際にどの様な関数が当てはまるのかを豊富なグラフ(イラスト)で紹介しました。
<わかる・できる様になる事>:それぞれの関数の意味と見分けができ、それを実際に定積分の計算や積分方程式・不等式の証明問題などに応用する事で、計算スピードの大幅な向上とミスを減らす事ができる様になります。
目次(タップした所へ飛びます)
偶関数と奇関数って何?【内容理解編】
さて、”偶関数”と”奇関数”とはどの様なものか、この項でグラフとともに詳しく解説していきます。
偶関数の意味と具体例
初めは最も単純な、『整式で表された関数』の場合で考えて見ましょう。
偶:偶数の偶であることからも分かりますが、\(f(x)=x^{2},x^{4},\cdots\)の様に、”べき乗”の部分が”偶数”の場合、その関数は偶関数となります。
もう少し一般化した定義を紹介します。
『f(x)=f(-x)が成り立つ場合、このf(x)は”偶”関数である』と言います。
また、非常に重要な特徴として、『”y軸”(=つまり、x=0)に関して、y=f(x)のグラフが対称である』というものがあります。
苦手な人はこの辺りで??となってしまうのですが、難しく考えず簡単な例・グラフを使って説明します。
例えば\(f(x)=x^{2}\)の最も基本的な二次関数の場合で考えてみると、\(f(1)=(1)^{2}=1 、f(-1)=(-1)^{2}=1\)
(カッコの中)に注目して見てください。1と”−1”でf(x)とf(-x) の関係になっている事がわかります。
そして、これら二つは結局2乗されるので『=1』と同じ値になります。→f(x)=f(ーx)の意味。
これは、\(x=2,3,4\cdots \)となっても、\(f(2)=f(-2)=4,f(3)=f(-3)=9,,,\)と、いかなるxに対しても常に成り立ちます。
特にややこしいことを言っているわけではない事が分かってきましたでしょうか?
次に、最大の特徴と紹介した、『y軸に関して対称』についても考えていきます。
”〜に関して”とか、〜に対称。という言葉は後にして、まずはイメージ図(視覚)で理解して見ましょう。
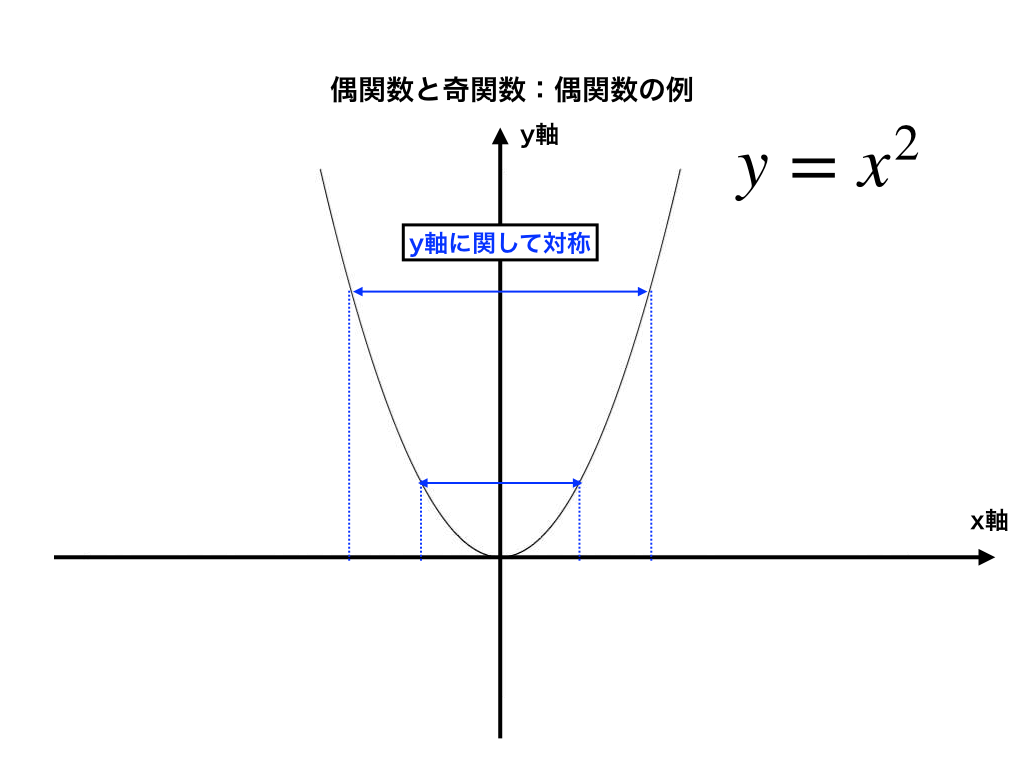
上の様に、f(x)=f(ーx)をグラフにすると『y軸に鏡を置いたように左右対称になる』と言っているだけです。
様々な偶関数と代表的な関数のイメージ
ところで、偶関数には(xの偶数乗)以外にも『cosx』を始めとして数種類の関数が当てはまります。
数三まで学ぶ人は、特に三角関数について注目して見てください。

奇関数の意味と具体例
ふたたび、整式で表された関数の場合で「奇関数」を考えて見ましょう。
奇:この場合も奇数の奇から、\(f(x)=x^{3},x^{5},\cdots\)と"べき乗部分"が"奇数"のとき、その関数は《奇関数》となります。
先ほどと同様に一般化してみます。
f(x)=-f(x) が成り立つならば、その関数f(x)は奇関数です。
こちらも基本的な例で解説していきます。
\(f(x)=x^{3}\)の場合で考えてみると、\(f(1)=(1)^{3}=1 、f(-1)=(-1)^{3}=-1\)
奇数乗されると、今度は『1』と『−1』になりました。
\(f(2)=(2)^{3}=8 、f(-2)=(-2)^{3}=-8\)でも、『8』と『ー8』で符号が逆転しています。
これが、f(x)=ーf(ーx)の意味なのです。
また、奇関数も偶〃と”ほんの少しだけ”異なる(だから混同しやすいのですが)特徴があります。それが、『”原点”(0,0)に関して、y=f(x)のグラフが対称』というものです。
以下で、『原点に関して対称』を同じく見ていきます。
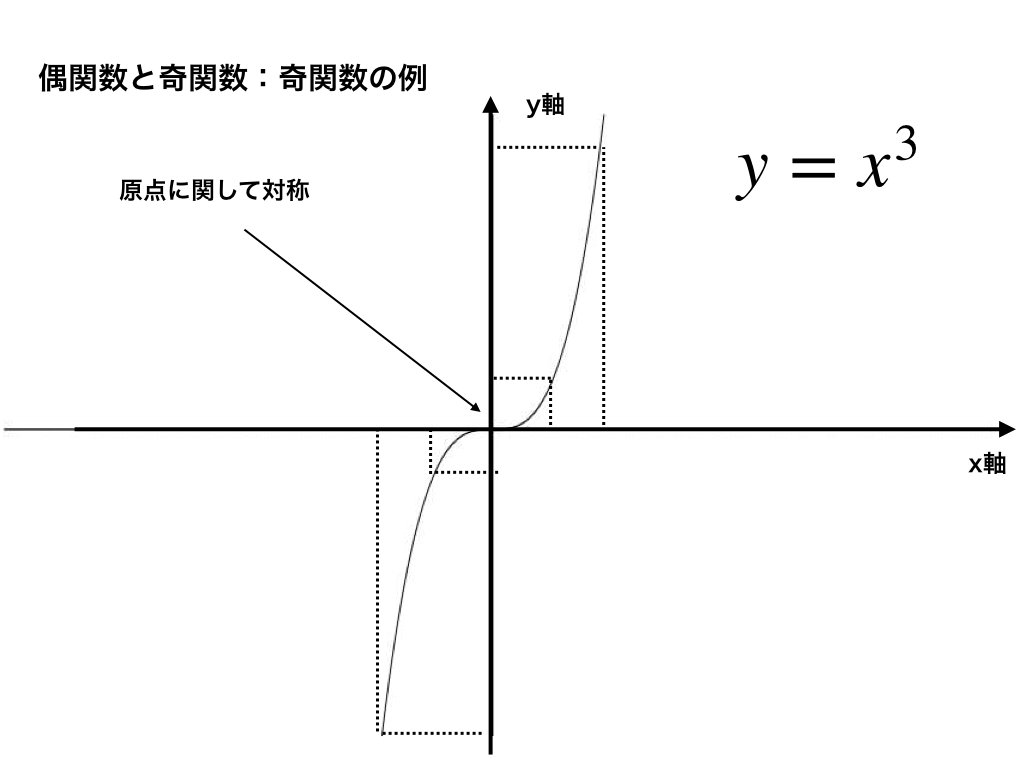
「原点に関して対称」
上の図のように、これは見たほうが頭に入りやすいかと思います。
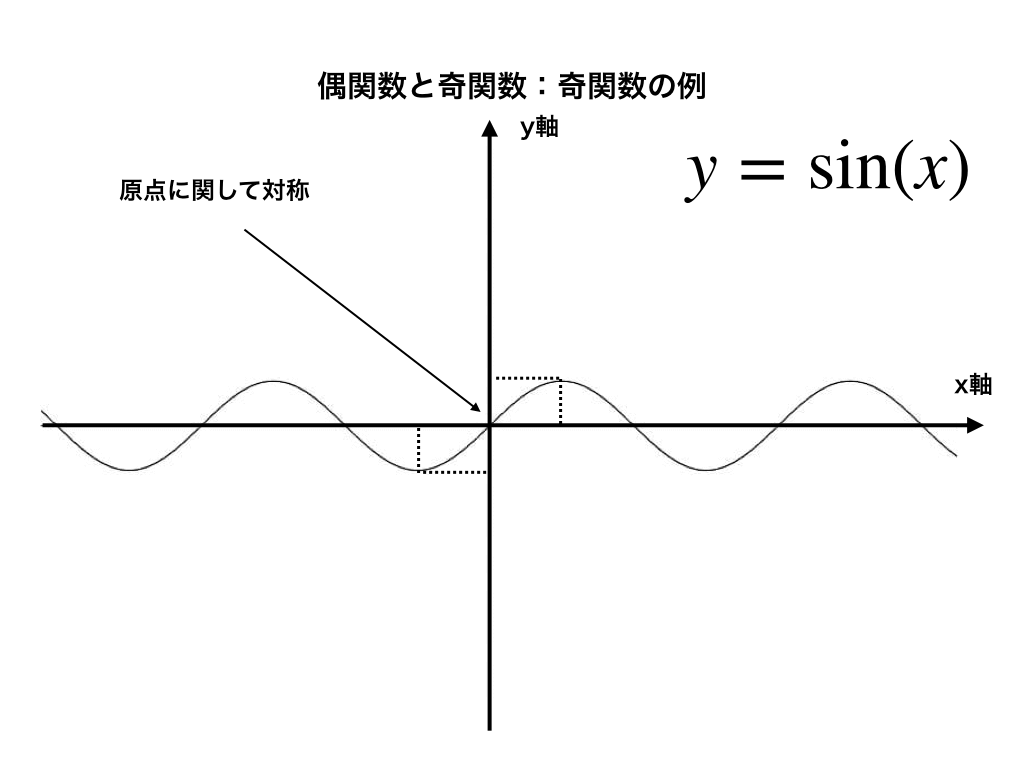
様々な奇関数と代表的なイメージ
代表的な奇関数は、『sinx』が挙げられます。(下のイメージ図参照)
積分に応用してみる【実践編】
ここまで、それぞれの定義や例を紹介してきましたが、本当に役に立つのはここからです。
積分の問題で計算ミスが多い、という人には効果が非常に大きいはずです。
定積分と偶・奇それぞれの関数
これから紹介することは、偶関数・奇関数を定積分する際に「積分区間が”1からー1”や”αからーα”の様に、符合は異なるが絶対値を取ると同じになる」という条件の時に成り立ちます。
<偶関数の場合>
これらも図を見ながら理解していきましょう。
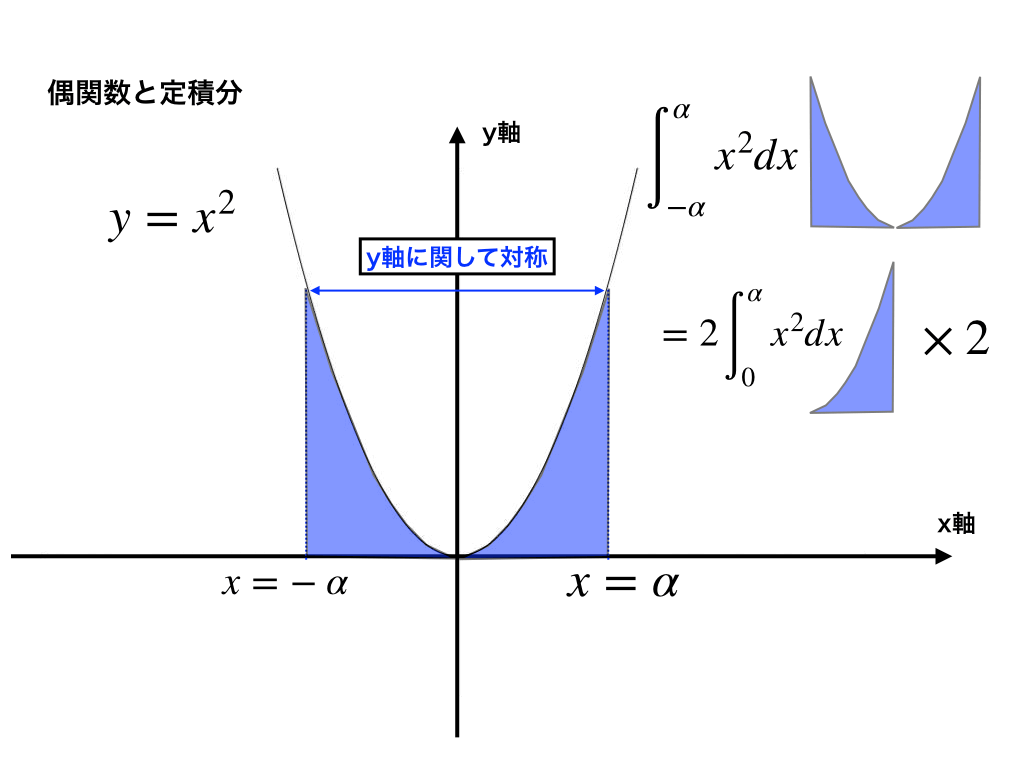
上の様な場合、α→0までの面積と0→ーαまでの面積は同じになるので、わざわざα→ーαを計算せずに、(α→0間の面積)×2で求めることができます。
<奇関数の場合>
奇関数のときには、さらに便利に計算できます。
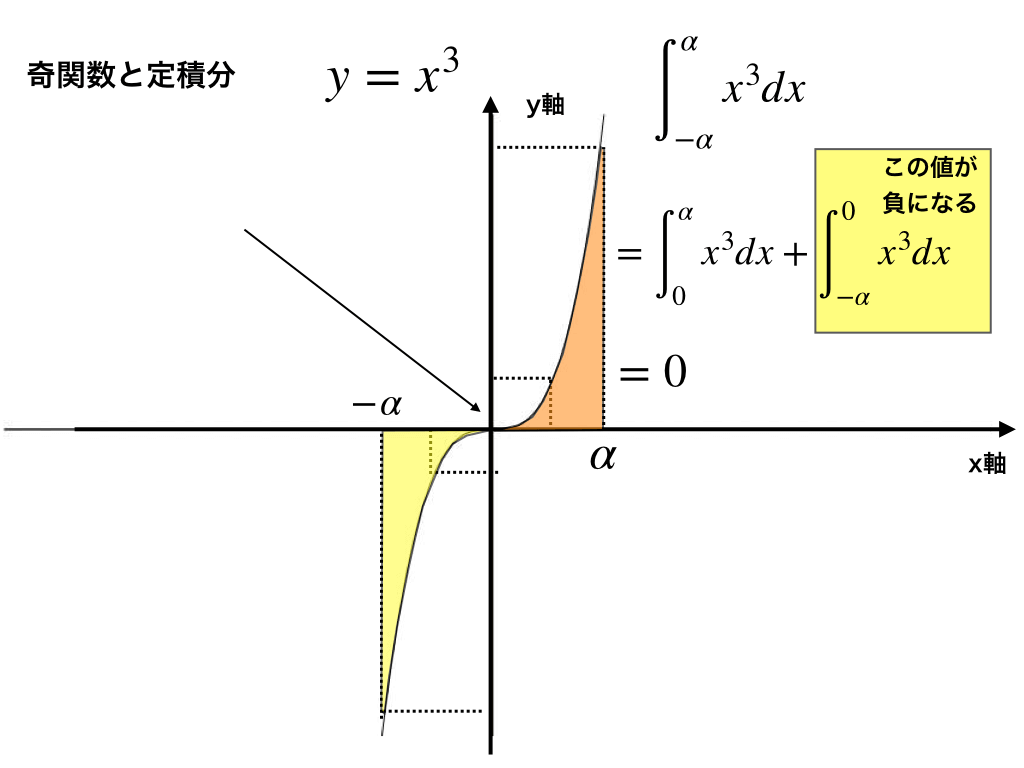
オレンジの部分と黄色の部分は同じになりますが、図中にも書いた様に、積分区間が0→αのとき負の値をとるので、結局\(\int^{\alpha}_{\alpha}f(x)dx=0\)となります!
定積分の(計算)問題
ここから、実際の問題を通して上で見てきた偶/奇関数の便利さを紹介します。
<問題>:次の定積分:$$\int^{2}_{-2}x^{5}+5x^{4}+2x^{3}+\frac{3}{5}x dx を求めよ。$$
解説とその威力
これは地道に計算すれば解く事が可能です。(下)
$$=[\frac{x^{6}}{6}+x^{5}+\frac{x^{4}}{2}+\frac{3x^{2}}{10}]^{2}_{-2}$$
しかし、さらにややこしい関数や、分数の係数がついていたり、代入する値が複雑になると、
・かなり計算ミスの恐れが高くなる上に
・時間ばかりがかかって、
メリットが一つもありません。
そこで、先ほど紹介した【偶関数】と【奇関数】の定積分の考え方を用います。
すると、\(x^{奇数乗}\)であることより、バッサリと\(x^{5}+2x^{3}+\frac{3}{5}x を=0\)として消してしまう事ができます!
さらに、\(x^{偶数乗}\)の部分は"2→0"を計算して2倍すれば・・・
$$2\times\int^{2}_{0}5x^{4}dx=2[x^{5}]^{2}_{0}=64$$
と、かなり簡単に求めることが出来ました。
(※:続編「1/6公式と関連する公式の紹介と『実践的な工夫』のコツ」を作成しました。偶関数・奇関数と合わせて利用することが出来れば、さらにspeed up &ミスを減らすことができます!)
積分方程式・不等式への応用
次は証明問題での使い方を解説します。
(参考:「積分方程式はたった二通りの解法で解ける!」)
問題:積分と不等式の証明
証明問題:いま、定数a,b,cを正の実数とし、\(f(x)=ax^{2}+bx+c \)で表される関数がある。
この時、次の不等式が成り立つことを示せ。
$$bc\int^{2}_{-2}\frac{f'(x)}{a}x dx <\int^{2}_{-2}(f(x))^{2}x dx$$
解説
<指針>:不等式の証明の王道の解法である、『移項して』→『(右辺)ー(左辺)>0』ならば(左辺)<(右辺)を利用します。
が、すぐにわかるかと思いますが、計算が非常に煩雑です。。。
$$(左辺)=\int^{2}_{-2}2bcx+\frac{b^{2}x}{a}dx$$
$$(右辺)=$$
$$\int^{2}_{-2}ax^{5}+2abx^{4}+(2ac+b^{2})x^{3}+2bcx^{2}+c^{2}x dx$$
さすがに(右辺)のほうはまともに計算したくないですね。。。
そこで、「奇関数の定積分」の何回め?かの出番です。
まず(左辺)にある\(\frac{b^{2}x}{a}=0\)とできるので、$$2\times [\frac{2bc}{3}x^{3}]^{2}_{0}=\frac{32bc}{3}$$
つぎに(右辺)のうちxの奇数乗の部分を全て=0とし(コレだけで計算量が全くことなって来ます。)偶数乗の部分だけ計算を進めると、
$$(右辺):2\times[\frac{2ab}{5}x^{5}+\frac{2bc}{3}x^{3}]^{2}_{0}$$
結果として$$(右辺)=\frac{128ab}{5}+\frac{32bc}{3},(左辺)=\frac{32bc}{3}$$
\((右辺)ー(左辺)=\frac {128ab}{5}\)とa,bは条件文より正なので、たしかに
$$bc\int^{2}_{-2}\frac{f'(x)}{a}x dx <\int^{2}_{-2}(f(x))^{2}x dx$$
が示せました。
まとめと微積分の関連記事へ
いかがでしたか。特に後半になるにつれて、その威力がよく理解できたのでは無いでしょうか。
今後も微積分の問題にあたる時は、偶関数・奇関数や積分区間に注意を払って、計算を優位に進めましょう!
微積がもっと得意になる記事一覧
微分・積分の記事まとめ>>「数2・数3の微積分の解法・解説記事まとめ」
極限から微積分へ>>「極限の解説記事6選!」
「スマナビング!」では、読者の皆さんのご意見・ご感想の募集を【コメント欄】にて行なっています。
(※):現在個々の問題のご質問に関しては、時期的に対応できない場合がございます。その他の誤植やご意見・ご感想は引き続き募集しています。
・お問い合わせ/ご依頼/その他のご連絡は、【運営元ページ】よりお願いいたします。

