部分分数に分解する方法と数列の和・極限・積分への応用まで
「部分分数分解があまり得意でない」、「どうやって分解すれば良いのか、又、分解後の分数の前にある係数はどの様に求めるのかわからない!」という人は多いです。
この記事をご覧になっているあなたも、苦手意識を持っているのではないでしょうか?
実際にはやり方の手順はほぼ決まっています。
この記事では、詳しく手順と方法を解説しているので、ぜひ道具として使いこなせるようになりましょう!
また記事の後半では、応用の仕方(数列の和・極限・積分法etc,,,)を実例を挙げながら紹介しています。
ぜひ最後までじっくりご覧下さい。
目次(タップした所へ飛びます)
部分分数分解とは
はじめに、「部分分数分解」とは何か?というもっとも基本的なところから説明していきます。
例えば以下のように分母が(xの式1)(xの式2)のような「かけ算」になっている一個の分数を
【(分母が(xの式1)の分数)ー(分母が(xの式2)の分数)】のように文字通り「分解」して、より簡単な(次数の低い)分数同士の引き算の形にすることを「部分分数分解」と呼びます。
$$\frac {1}{( xの式1)× ( xの式2)}=\frac {1}{(xの式1)}-\frac {1}{( xの式2) }$$
部分分数分解のやり方:具体例
具体的にやり方を見てみましょう。
$$\frac {1}{x( x+2) }=\frac {1}{2}\{ \frac {1}{x}-\frac {1}{( x+2) }\}$$
左辺が部分分数に分解する前の式、左辺が分解後の式です。
試しに、右辺を通分して、左辺を導いてみて下さい。確かに元の分数に戻ることがわかると思います。
どうやって係数を求めるか
ここで、$$\{ \frac {1}{x}-\frac {1}{( x+2) }\} $$の頭についている”係数の2分の1(1/2)”がどこから出てきたか分からなかったり、
自分で部分分数に分解するときに、うまく係数が求められない人のために「係数を求める方法」を次の項で解説します。
部分分数に分解する手順とコツ(係数を求める方法)
$$\frac {1}{x(x+2) }=\frac {1}{2}\{ \frac {1}{x}-\frac {1}{( x+2)}\}$$を使って、手順を書くと、
1:分解された後の分数を先に作り
とりあえず、分解後の式を作ります。
$${ \frac {1}{x}-\frac {1}{( x+2) }}$$
2:分子を適当な文字で置く
この際に、係数(=分解後のそれぞれの分数の分子)がわからないので、文字でおきます。
$${ \frac {α}{x}-\frac {β}{( x+2) }}$$
今回は、それぞれ分子をα、βとおきました。
3:左辺と右辺は同じなので係数を比較する
ここで、左辺$$\frac {1}{x( x+2) }$$と右辺$${ \frac {α}{x}-\frac {β}{( x+2) }}$$
は同じ式(恒等式;詳しくはパターン3で説明しています)なので、右辺を通分します。
$$\frac {( x+2) α -xβ }{x( x+2) }$$
さらに、左辺のxの係数と定数項=右辺のxの係数と定数項になるので、
$$\frac {( x+2)α-xβ }{x( x+2) }=\frac {1}{x( x+2 }$$
分子を比較すると、xの係数は(α-β)=0、定数項は2α=1
より、α=1/2,β=1/2
従って、これをはじめに作った分解後の式に代入することで、
$$\frac {1}{x(x+2)}=\frac {1/2 }{x}-\frac {( 1/2)}{x+2}=\frac {1}{2}(\frac {1}{x}-\frac {1}{x+2})$$
このように、うまく2つの分数に分解できました。
色々な分解のパターンと係数比較
前の項で紹介した部分分数分解(の形)はもっとも簡単なタイプです。
他にもいくつか有名な形があるので、ひとつずつ紹介していきます。
(※)色々なタイプがありますが、基本的に分解の流れは上の1通り:(分解後の分数を作り→分子を文字でおく→係数比較を行って整理する)です。
パターン2:(分子がax+b)になっている
$$\frac {5x+3}{( 3x+2) ( 2x+1) }=\frac {α }{3x+2}-\frac {β }{2x+1}$$
このタイプは、分子が定数項(xなどの変数で無いもの)だけだった、
パターン1と異なり、分子にxの一次式が入っています。
手順は、
まず$$\frac {α}{3x+2}-\frac {β}{2x+1}$$を作り
文字でおき、
$$\frac {(2x+1)α-( 3x+2) β}{(3x+2) (2x+1)}$$
通分して、係数比較です。
5x+3=( 2α -3β) x+( α -2β)
ゆえに、
・2α-3=5,
・α-2β=3
の連立方程式を解いて、
α=1、β=−1
最後に、元の式のαとβに求めた数字を代入すると、
(注意!:このときβ=−1なので、部分分数分解をしたのちの、2つの分数は引き算ではなく足し算になっています。)
$$\frac {5x+3}{(3x+2)(2x+1)}=\frac {1}{3x+2}+\frac {1 }{2x+1}$$
このようになり、上手く分解できました。(検算として、左辺←右辺をしてみて下さい。)
3つの分数に分解する (パターン3)
つぎは、3つの分数に分解するタイプです。この場合も基本的な手順は変わりません。
が、先に作っておく“分解後の分数の分母”が少し異なります。
$$\frac {1}{( x+3)( x+2) ^{2}}=\frac {α}{( x+3) }-\frac {β }{( x+2) ^{2}}-\frac {γ}{( x+2) }$$
分母を払って、
$$1=\frac {( x+2) ^{2}α-( x+3) β -( x+3)( x+2) γ}{(x+3)( x+2) ^{2}}$$
あとは、同様に連立方程式をたててα、β、γを求めることが王道です。
しかし、このパターンのように少し複雑なものの場合は、
両辺がつね(恒)に(等)しい式(どのようなxを代入したとしても式が成り立つ「恒等式(**)」である)事を利用して、
分母を払った式のxに、適当な数字を代入する事でかなり簡単に(α、β、γ)を求めることができます。
イメージとしては、因数定理を使ってあまりを求めるときと似ています。
<参考:「因数分解のパターン(の因数定理の部分)」>
今回は、\(1=(x+2)^{2}α-(x+3)β-(x+3)(x+2)γ\)
の式にx=-2、-3、0をそれぞれ代入する事で、
1=ーβ
1=α
1=γ と求まります。
よって、$$\frac {1}{(x+3)(x+2)^{2}}=\frac {1}{( x+3) }+\frac {1}{(x+2)^{2}}-\frac {1}{(x+2)}$$
部分分数分解の数列の和/無限級数/積分への応用
ここからは、上で学んだ分数の分解をする理由(とメリット)を実例とともに紹介していきます。
特に数3まで勉強する理系の方にとって、非常に役立つことがわかるかと思います。
数列の総和への応用
数列の和を求める際に部分分数に分解すると、
途中の式が綺麗に消えてくれることで、非常に簡単に総和を求めることができる場合があります。
<参考:「数列の和とシグマ公式の覚え方・使い方」>
数列の総和への応用例
今、一般項:\(a_{n}=\frac{1}{n(n+2)}\)の数列を初項から第n項まで足し合わせることを考えます。
数式で表すと右のようになりますね:$$\sum ^{n}_{k=1}\frac {1}{k( k+2) }$$
この数列は一般項のカタチは、明らかに部分分数に分解できるので(*1)、
$$\frac {1}{n(n+2) }=\frac {1}{2}(\frac {1}{n}-\frac {1}{n+2})$$
$$より、\sum ^{n}_{k=1}a_{k}=\sum ^{n}_{k=1}\frac {1}{2}(\frac {1}{k}-\frac {1}{k+2}) $$
少し書き出してみると・・・
$$\sum ^{n}_{k=1}\frac {1}{2}( \frac {1}{k}-\frac {1}{k+2}) $$
$$=\frac {1}{2}\{ \frac {1}{1}-\frac {1}{3}+\frac {1}{2}-\frac {1}{4}+\frac {1}{3}-\frac {1}{5}+\ldots $$
$$+\frac {1}{n-1}-\frac {1}{n+1}+\frac {1}{n}-\frac {1}{n+2}$$
ちょうど、$$-\frac {1}{3}-\frac {1}{4}+\frac {1}{3}\ldots +\frac {1}{n-1}+\frac {1}{n}$$この部分が打ち消しあって、消えてくれる事がわかります!
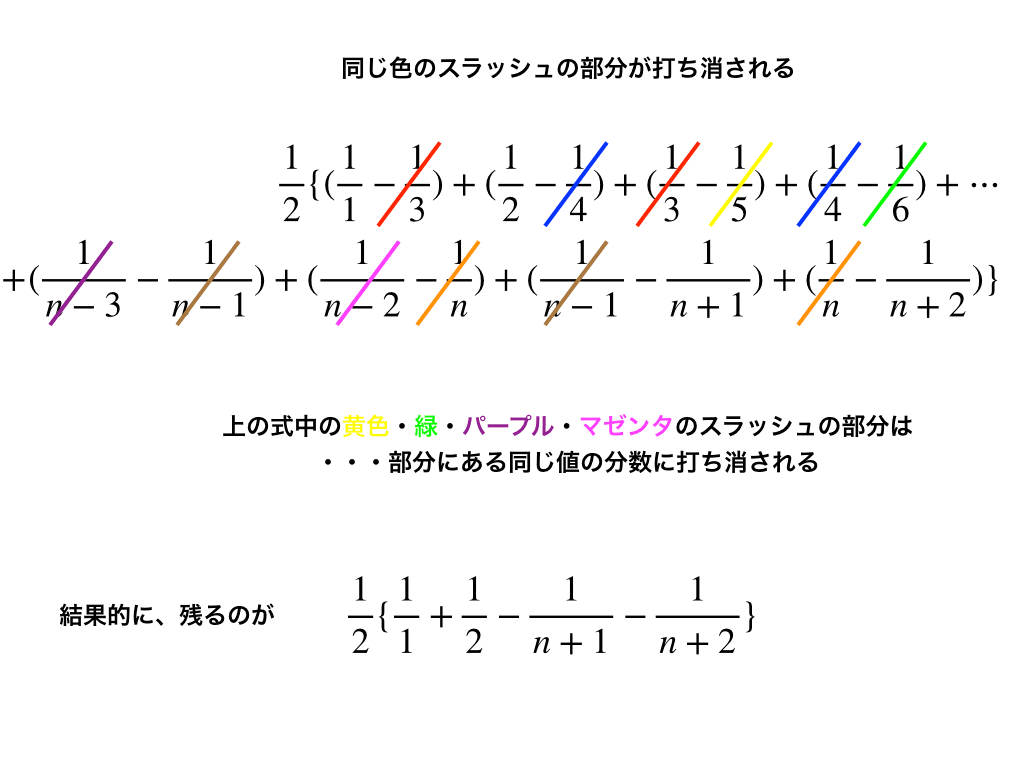
$$従って、\sum ^{n}_{k=1}a_{k}=\frac {1}{2}(1+\frac {1}{2}-\frac {1}{n+1}-\frac {1}{n+2})$$
$$=\frac {3n^{2}+5n}{4n^{2}+12n+8}$$
((*1):色々と類題をこなしていくと、『この問題は部分分数分解を利用して解くことが出来る』とわかるようになって来ます!)
次の項では数列の和と「極限」の融合を見ていきます。
極限への応用(一般項が分数の数列の無限級数)
数学Bでは、数列の和はある項や第n項までを足し合わせていましたが、数三の極限では
\(\lim _{n→\infty }S_{n}\)
つまり、n→∞:無限個足し続ける事を考えます。(これを無限級数と言います)
<無限級数=(数列の和の極限)について詳しくは→「数列を無限に足し合わせる:無限級数・無限等比級数とは」>
無限級数の例
先ほどの「数列の和」で扱った、一般項の無限級数を求めてみます。
すでに、$$部分和S_{n}=\frac {3n^{2}+5n}{4n^{2}+12n+8}、$$の形になっているので
無限級数はその極限をとって、$$=\lim _{n→\infty}\frac {3n^{2}+5n}{4n^{2}+12n+8}$$
とすればよく、答えは、3/4,となります。
(無限級数と、不定形については上のリンクと→「数列の極限:不定形の解消法がわかる」を参考にして下さい。)
分数で表された関数の積分への応用
数学3での積分では、分数関数を積分することが頻繁にあります。
この場合も、“部分分数分解”を利用することによって、次数が下がったり、別の公式が使える形に変形できたりします。
分数関数の積分の例
$$\int \frac {1}{x^{2}-9}dx$$
$$\int \frac {1}{( x+3)( x-3) }dx$$
実際にこの関数を部分分数に分解したうえで、積分して見ましょう。
$$=\frac {1}{6}\{ \frac {1}{( x-3) }-\frac {1}{( x+3) }\} $$
$$\frac {1}{6}\int \frac {1}{( x-3) }-\frac {1}{( x+3) }dx$$
=1/6( log|x-3|-log|x+3|)+C 、ただしCは積分定数
$$=\frac{1}{6}log \frac{|x-3|}{|x+3|}+C$$
この積分は半分公式の様に紹介されていますが、部分分数分解を利用しても求めることができます。
部分分数分解のまとめと関連記事(数列:極限:積分)
・後半の数列の和、無限級数、積分(数3)で触れたように部分分数分解は非常に重要なツールになっていきます。
・(特に数3まで学ぶ人)は自由自在に使いこなせないと、計算の途中で解けなくなってしまうので、
なるべく早いうちに多くの類題、応用題を使ってマスターするようにしましょう。
・続編では、積分との融合問題や計算テクニックについてさらに深く掘り下げます(現在作成中)
今回も最後までご覧いただきまして、本当に有難うございました。
・当サイト「スマホで学ぶサイト、スマナビング!」は皆さんのご意見や、
SNS上での反応などをもとに日々改善、記事の追加、更新を行なっています。
・ご質問・ご意見がございましたら、コメント欄までお寄せください。
また、snsでいいね!やシェア、Twitterのフォローをしていただけると助かります。
・より良いサイト運営と、記事作成の為にぜひご協力お願い致します!
・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページよりお願い致します。