対偶とは?対偶法のコツと逆/裏との関係を分かりやすく図で解説

対偶法(論理と集合・証明シリーズ)

高校数学・大学入試で用いる証明法は色々とありますが、

その中でも最も重要な3つの証明法：数学的帰納法・背理法・対偶法を解説しています。

バックナンバーは＞＞

・「数学的帰納法の解説記事」・

・「背理法の解説記事」＜＜より。

今回は、「対偶法」を扱います。具体例やイラストを見ながら一つ一つ理解を進めましょう。

用語の解説の後に、実際に問題を利用して確認していきます。

対偶とは？逆・裏やド・モルガンの法則との関係

「対偶法」を学ぶ前に、論理と集合の範囲の言葉の意味を知っておく必要があります。

$$命題:p→q(pならばq)$$

真と偽

命題(p→q:pならばq)が正しいことを『真』、

間違っていることを『偽』と言います。

逆とは

「逆」とは、命題の矢印の向きが逆の事を言います。

『p→q』の“逆”は『q→p』と書き、「q、ならば、p」と読みます。

裏とは

「裏」は元の命題を否定したものです。

$$『p→q』の裏は『\overline {p}\rightarrow \overline {q}』$$

と書き、「p、で無いならば、qで無い」と読みます。

＜否定のバー（元の命題と裏）の図＞

対偶とは

いよいよこの記事のメインである『対偶』です。

$$『p→q』の対偶は「\overline {q}\rightarrow \overline {p}』$$

「q、で無いならば、pで無い」（下の図を見てください）

対偶の最も重要な性質が、【元の命題とその命題の対偶の真・偽が必ず一致する】と言うものです。

「敵の敵は味方」の様な理屈で考えると分かりやすいでしょうか？

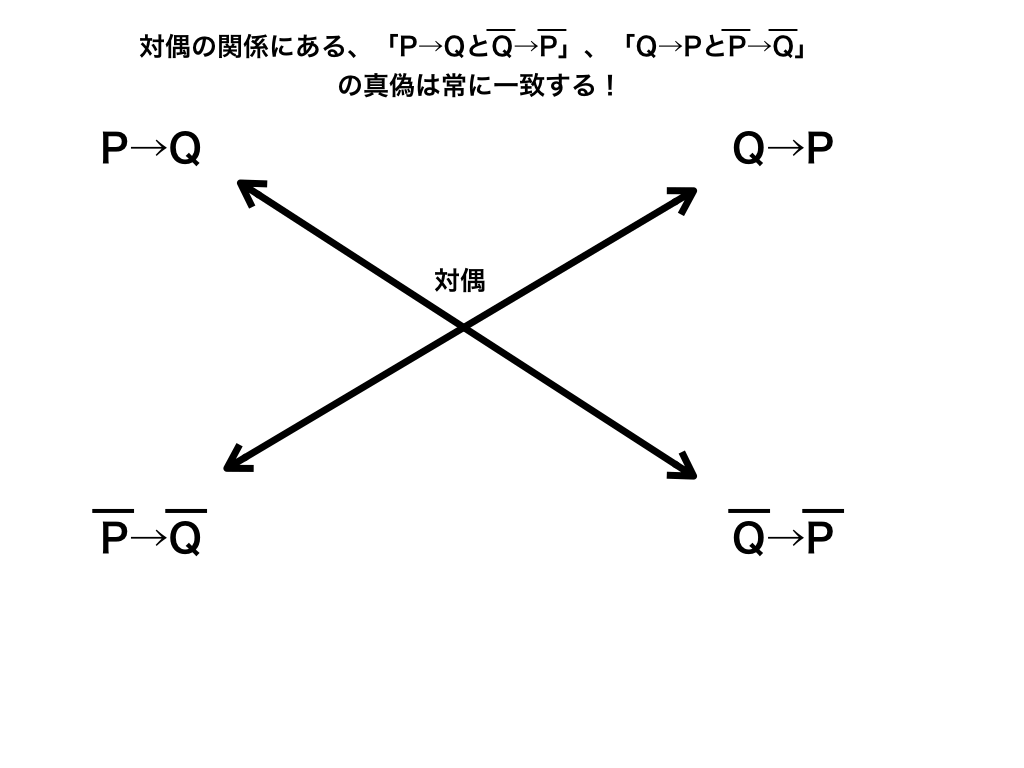
＜元の命題とその対偶の関係図＞

この性質を利用して、そのまま真・偽を判定(or証明)しにくい命題の対偶を調べて

、間接的に証明する方法が【対偶法】です。

逆/裏/対偶の関係図(まとめ)

ここまでで紹介して来た、「逆・裏・対偶」の関係をまとめて図にしたものが下の＜図１＞です。

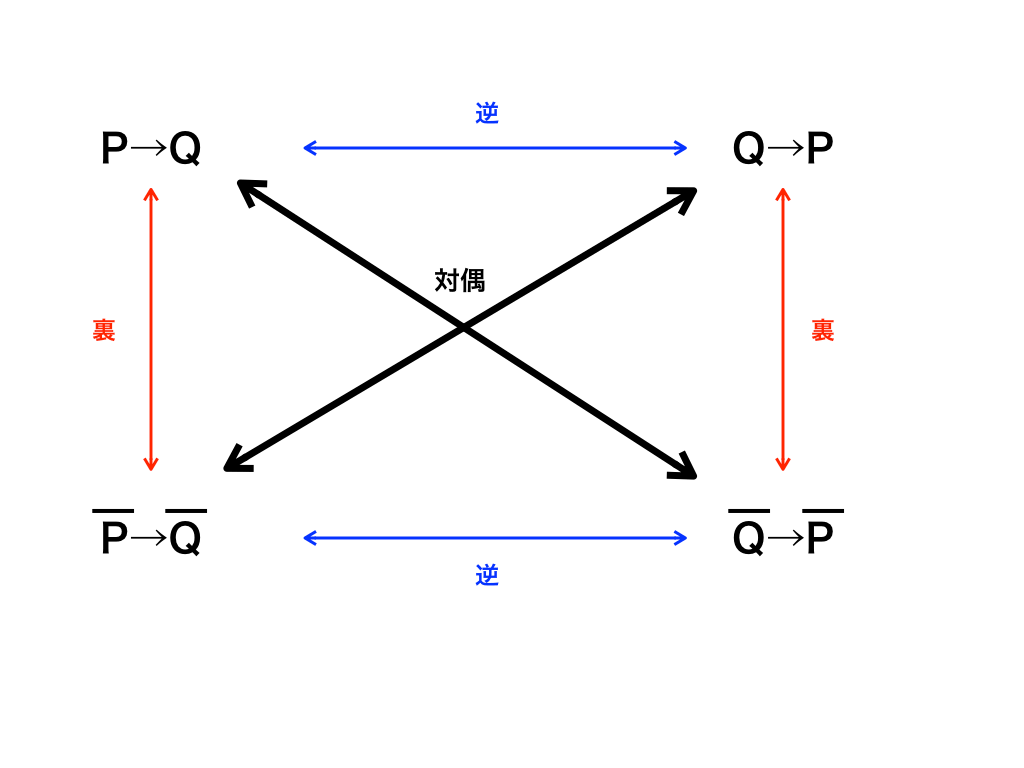
＜図１：逆・裏・対偶の関係図＞

さて、文字ばかり並ぶと分かりにくくなりますから、１つの命題(のこと)を例にして解説していきます。

対偶法の使い方・コツ

では実際に、どのように対偶法を用いて証明を進めるのか、簡単な例題をもとに考えていきます。

命題１

命題:「n²が2の倍数、ならば、n=2の倍数である」を証明せよ。

これを文字で表すと

『n²＝2k→n=2k(kは整数)』となり、

今までpで表していた部分が、n²＝2k、（n²が2の倍数)

”→”の矢印が「ならば」の意味、

qが【n=2k(kは整数)】に対応しています。

さて、この命題を証明するにあたって、これまで学んできた「背理法」・「数学的帰納法」、

そして今回の「対偶法」など、色々な方法の中から証明法を選択する必要があります。

対偶法を選ぶ目安『矢印の向きを逆にした方が証明が楽になるか？』

初めのうちはどの方法を使って証明すれば良いのか？と悩むかもしれません。

が、一つの目安として『pならば→qである』を『qでないならばpでない』

に変えた方が単純になる/ならない、という点で命題を見てみることをお勧めしています。

つまり、この命題１を考えると、

（証明する命題）「n²が2の倍数ならばn=2の倍数である」と、

（証明する命題の対偶）「n=2の倍数でないならばn²が2の倍数でない」

となって、二乗が外れた分だけ少し簡単になります。

よって、この問題は対偶法で証明していくことにします。

では解答を作っていきます。

解答・解説1

この命題の対偶を取ると、『n＝2の倍数で無いならば、n²は2の倍数では無い』となる。

＜この様な倍数が絡む時は、剰余類に分けると上手く行く事が多いです

＜参照:「整数問題の重要解法(2)剰余類に分けてみる」＞

ここでは、nが2の倍数でないことをn=2k+1(kは整数)と表します。

これを\(n^{2}\)に代入すると、

\((2k+1)^{2}=4k^{2}+4k+1\)

式変形して、\(n^{2}=2(2k^{2}+2k)+1\)

これは(2の倍数)+１の形なので、n²は常に2の倍数でない。
よって、対偶が真なので元の命題も真。

以上より『n²が2の倍数ならばn=2の倍数である』が示された。

命題２：定着用問題（対偶法）

命題：「m²+n²+l²≠０、ならば、m,n,lのいずれかは０でない」を証明せよ。

この命題も対偶法を用いて証明します

（対偶法を選んだ理由；『m,l,nのいずれかは０でない』の部分に注目すると、その裏は『m,l,nの３つの文字全てが０』となり、元よりも格段に証明しやすそうになっている事がわかるでしょうか？）

ではここから、少し時間をとって自分なりに証明して見てください。

・・・

・・・

解説していきます。

対偶は、「m,n,lが全て0、ならば、m²+n²+l²=0」

『いずれか』の反対は『全て』です。

m=0,n=0,l=0・・・（１）

\(\mathrm{（１）をm^{2}+n^{2}+l^{2}}に\)

それぞれ代入すると、

\(０^{2}+0^{2}+0^{2}=0より真。\)

したがって、対偶が真なので、元の命題である

「\(m^{2}+n^{2}+l^{2}≠０\)ならば、m,n,lのいずれかは０でない」も真

よって示された。

この命題は、直感的に正しいことがわかるかと思います。

が、実際証明するとなると、対偶を取った方が圧倒的に楽です。

まとめと背理法・数学的帰納法との関係

・逆・裏・対偶の関係をもう一度図を見て頭の中で整理しておきましょう。

（特に『逆』と『裏』はどっちがどっちかあやふやになりやすいので要注意です！）

・対偶法を使うべきかどうか判断するには、”とにかく対偶をとって元の命題との難易度を比べてみる”事がpointです。

〜証明シリーズ〜

以下に、もう一度主な証明法の記事をまとめておきます。

背理法

背理法は、真or偽を先に仮定してその矛盾を突くことで証明を進めます。

「背理法とは何か？キソと応用問題『tan1°は有理数か』」

数学的帰納法

数学的帰納法は、数列の分野や整数問題で頻繁に利用します。

まずn=k（整数）の時命題が成り立つと仮定し、その仮定を利用してn=k+1、すなわち”その次の数でも成り立つ”ことを示すことで全てのnで成り立つことを証明します。

（詳しくは以下の記事をご覧ください）

「数学的帰納法の解説と証明問題」

論理と集合の記事

「集合と写像とは？線形代数への道しるべ」

「ド・モルガンの法則と余事象の解説記事」

（NEW!）「必要条件と十分条件の見分け方、例題の解き方のコツ」

今回も最後までご覧いただき有難うございました。