
ベータ関数【難関大頻出】
<この記事の内容>:難関大・学部でテーマとして出題されやすい「ベータ関数:第1種オイラー積分」の証明問題を解きながら、その特徴や応用法などを解説していきます。(この記事は:「積分漸化式の4パターンと問題の解法」の続編です。)
<関連記事>:「数学3:微積分法まとめ」
目次(タップした所へ飛びます)
ベータ関数とは
一般的に、次のような式をベータ関数といいます。
$$B(p,q)=\int_{0}^{1}x^{p-1}(1-x)^{q-1}dx$$
そして、(p,q)を自然数に限定した場合(ここからはp=k,q=lとします)
が高校数学(難関大入試)で頻出です。
β関数の典型(証明)問題
\(B(k,l)=\int_{0}^{1}x^{k-1}(1-x)^{l-1}dx\)
かつ、k,lが共に自然数であるとする。
(1):B(k+1,l-1)とB(k,l)の関係式を導け。
(2):B(k,l)をkとlだけの式で表せ。(hints!【1】を利用する。)
(3):$$\int_{\alpha}^{\beta}(x-\alpha)^{k-1}(\beta-x)^{l-1}dx$$
$$=(\beta-\alpha)^{t}\frac{(k-1)!(l-1)!}{(k+l-1)!}$$を導け。
解説
いきなり自分で解くのは難易度が高いので、分からない人は解答・解説を見ながら流れをつかんでください。
なお、(1)では部分積分がKeyとなるので「部分積分の仕方とコツ”下箱法”を実例で解説」も併せてご覧ください。
(1):部分積分法の利用
以前に紹介した、「積分漸化式4パターンと問題の解き方」と同じく、ここでも部分積分を用いて『B(k-1,l-1)とB(k,l)の関係式』を作っていきます。
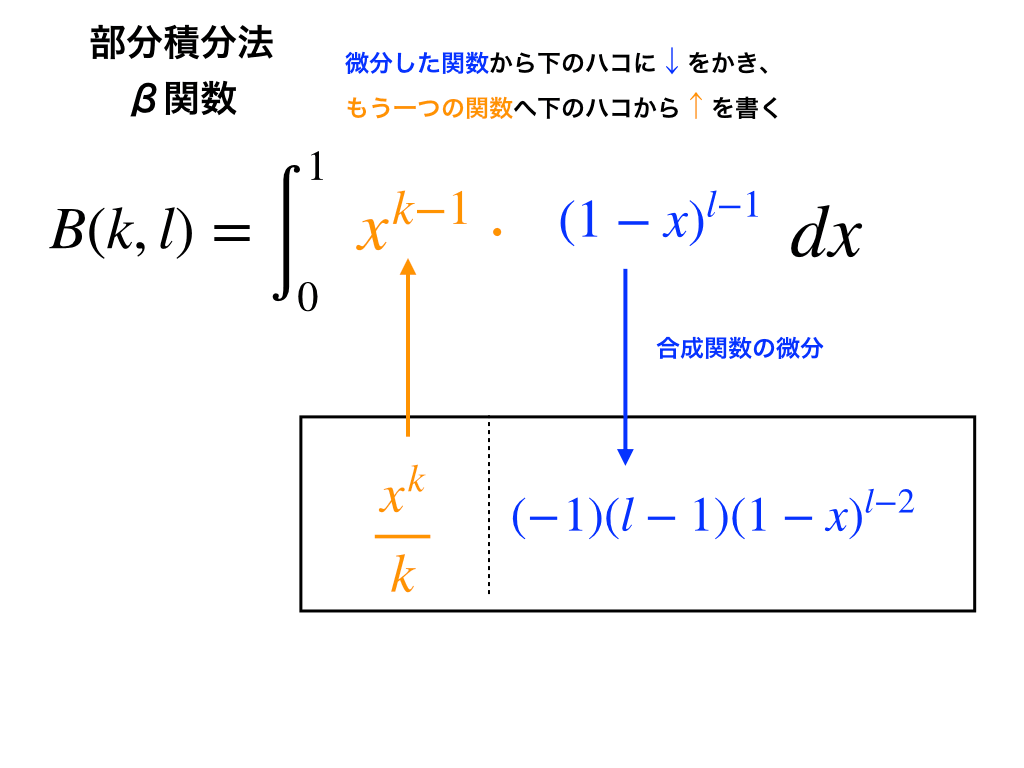
<上図1>のようにB(k,l)を部分積分していくと、
$$\int_{0}^{1}x^{k-1}(1-x)^{l-1}dx$$
$$=[\frac{x^{k}}{k}(1-x)^{l-1}]_{0}^{1}+\frac{l-1}{k}\int_{0}^{1}x^{k}(1-x)^{l-2}dx$$
左側は0〜1を代入すると=0となるので、結局
$$B(k,l)=\frac{l-1}{k}\int_{0}^{1}x^{k}(1-x)^{l-2}dx$$
ここで、\(x^{k}(1-x)^{l-2}\)はB(k+1,l-1)と書ける(xのk-1乗がk、1-xのl-1乗がl-2になっていることより)ので、
$$B(k,l)=\frac{l-1}{k}B(k+1,l-1)\cdots (答)$$
(2):関係式を繰り返し使用
さて、次はベータ関数をk、lの文字だけで表しましょう。
ここでのポイントは、(1)で作ったB(k,l)とB(k+1,l-1)の関係式をうまく使うことです。
$$B(k,l)=\frac{l-1}{k}B(k+1,l-1)\cdots (※)$$
(※)より、$$B(k+1,l-1)=\frac{l-2}{k+1}B(k+2,l-2)$$
左辺のB(k+1,l-1)を(※)の右辺に代入して、
$$B(k,l)=\frac{l-1}{k}\cdot \frac{l-2}{k+1}B(k+2,l-2)$$
これをB(k+l-1,1)になるまでどんどんと行うと、
$$B(k,l)=\frac{l-1}{k}\cdot\frac{l-2}{k+1}\cdots \frac{1}{k+l-2}B(k+l-1,1)$$
ここで$$B(k+l-1,1)=\int_{0}^{1}x^{k+l-2}(1-x)^{0}dx$$
の積分を行うと、$$=\frac{1}{k+l-1}$$
よって、$$B(k,l)=\frac{l-1}{k}\cdots \frac{1}{k+l-2}\cdot\frac{1}{k+l-1}$$
・・・(※※)
階乗の形を上手く使う(式変形のコツ)
ここで、(※※)をよく観察してみると、分母は(k+l-1)から一つずつ値が減ったものを掛け合わせているので、階乗の形\((k+l-1)!\)で表せます。
しかし、あくまで分母は”k”までであることから、\((k+l-1)!\)だけでは割り過ぎてしまうので、調整が必要です。
(具体的には、(-1)の部分が(-2,-3,,,,-l);つまり\((k+l-l)!を(k)!\)までにする必要があります。)
そのため、(k-1)から(1)までの部分を相殺する”\((k-1)!\)”で割ってあげれば上手くいきます。
一方(※※)の分子は単純に\((l-1)!\)で表せます。
よって、$$B(k,l)=\frac{(l-1)!}{\frac{(k+l-1)!}{(k-1)!}}$$この分母の(k-1)!を払ってあげることで
$$B(k,l)=\frac{(k-1)!(l-1)!}{(k+l-1)!}$$
とベータ関数を"kとl"の文字だけで表すことができました。
β関数の特徴と応用
さて、ここから興味深い公式が導けます。
(3):有名公式へ
次のように、ベータ関数によって(左辺)の積分が(右辺)のようなカタチで表すことができることが知られています。
$$\int_{\alpha}^{\beta}(x-\alpha)^{k-1}(\beta-x)^{l-1}dx$$
$$=(\beta-\alpha)^{k+l-1}\frac{(k-1)!(l-1)!}{(k+l-1)!}$$・・・(※※※)
この結果を少し変形してみます。
1/6公式へ
ここで、k=l=2を代入することで、
$$\int_{\alpha}^{\beta}(x-\alpha)(\beta-x)dx=(\beta-\alpha)^{3}\frac{(0)!(0)!}{(3)!}$$
$$\int_{\alpha}^{\beta}(x-\alpha)(\beta-x)dx=\frac{1}{6}(\beta-\alpha)^{3}$$
これは超有名公式「面積公式(1/6)」です!ベータ関数から馴染み深い式が導出できました。
とりあえず、(※※※)の式を簡単に示しておきましょう。
まず、(左辺)の$$\int_{\alpha}^{\beta}(x-\alpha)^{k-1}(\beta-x)^{l-1}dx$$
について。
このように、一見どのようにすれば証明できるのかがわからない場合、前の誘導に従うことを考えます。
ここでは、β関数に似せたカタチにできないか検討します。
すると、\((x-\alpha)^{k-1}\)の部分はほとんど同じ、\((\beta-x)^{l-1}\)もβが増えて-xになっていますが全体的には似た形をしています。
後は積分区間が異なるので、ここを揃えつつ上手く似せる方法を考えます。
\(u=\frac{x-\alpha}{\beta-\alpha}\)で置換し、x=の形に直して
\(x=(\beta-\alpha)u+\alpha\)
より、
$$\int_{0}^{1}(\beta-\alpha)^{k+l-1}u^{k-1}(1-u)^{l-1}du$$
これでほぼβ関数の形になりました。
あとは(β-α)の部分を前に出せば残りはB(k,l)で表せるので、
\(=(\beta-\alpha)^{k+l-1}B(k,l)\)
この\(B(k,l)=\frac{(k-1)!(l-1)!}{(k+l-1)!}\)を代入すれば(3)の式を導くことができます。
β関数まとめ
最後の『応用』や有名な面積公式が導出できただけでなく、このベータ関数と第二種オイラー積分(ガンマ関数)にはさらに興味深い性質があります。
興味がある人は是非大学などで更に詳しく学んでください!
関連記事・積分漸化式へ
最後までご覧いただきまして、有難うございました。
【受験・学習メディア】:スマホで学ぶサイト、「スマナビング!」では,読者の皆さんのご感想を募集しています。
ぜひコメント欄にお寄せください。 (※:個々の問題の質問等には対応出来ない場合があります。)
・その他の「お問い合わせ/ご依頼/タイアップ」等に関しましては《運営元ページ》にて、ご連絡をお待ちしています。

