
減衰曲線とその面積・応用
<この記事の内容>:いわゆる「減衰曲線」と意味とグラフのイメージ、さらに曲線と軸が囲む面積を求める方法を紹介しています。
<関連分野の記事>:「数学Ⅱ・Ⅲ微分・積分まとめページ」
目次(タップした所へ飛びます)
減衰曲線とは?
$$y=\int_{\alpha}^{\beta}(xの関数)\sin x dx$$で表されるような、徐々にx軸に近づいていく(受験問題では、“減衰はしていませんが”逆に徐々に大きく振動するような場合もあります。)曲線のことを言います。
基本的なグラフ
減衰曲線の中でも最頻出の\(y=e^{x}\sin x\)のグラフは以下の様になります。
\(y=e^{-x}\cdot\sin x dx\)
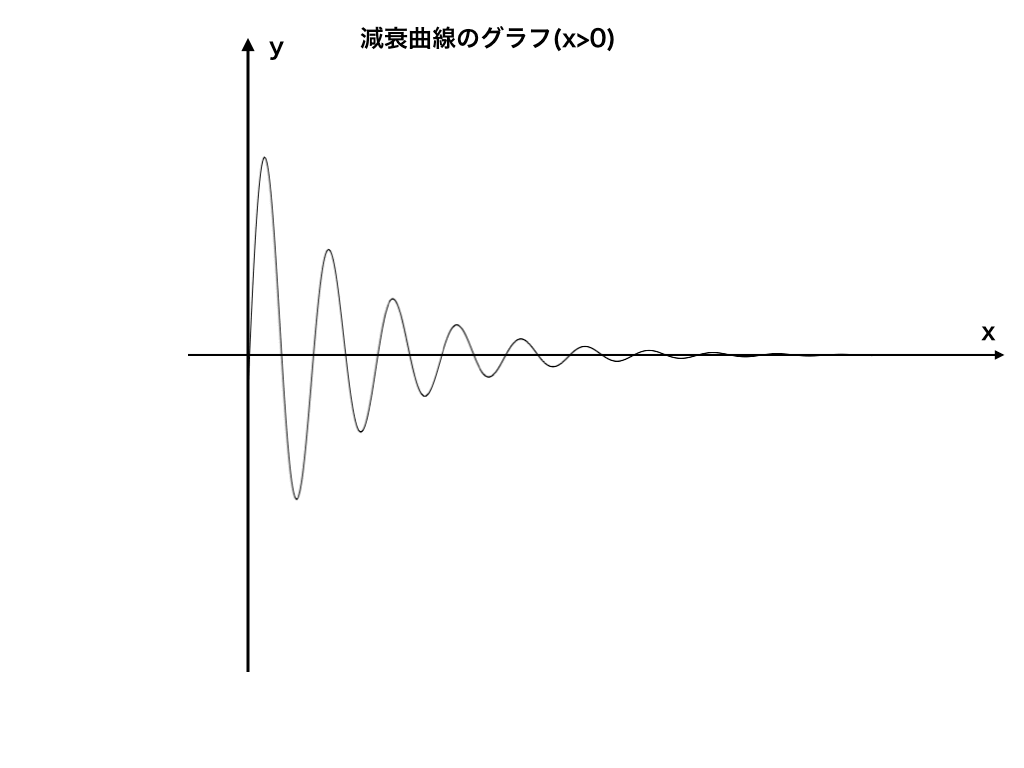
<図1>
(※:実際には、\(e^{-x}\)は急速に0に近付く為、上の図では上下方向に拡大しています。)
物理などでの応用(単振動と摩擦)
減衰曲線は数学だけでなく、様々な分野で登場しますが、高校で学ぶ範囲では、物理(力学)の「摩擦のある単振動」における物体の運動などがこれに当てはまります。
減衰曲線とx軸との面積を求める方法
ここからメインとなる求積問題の解説をしていきます。
\(e^{-x}|\sin x|\)の求積問題
問題1:\(y=e^{-x}|\sin x|\)とx軸が囲む面積を求めよ。
上の問題の三角関数の部分だけに絶対値をつけてみます。
ちょうどx軸から下の部分を全部折り返すので、グラフは以下のようになります。
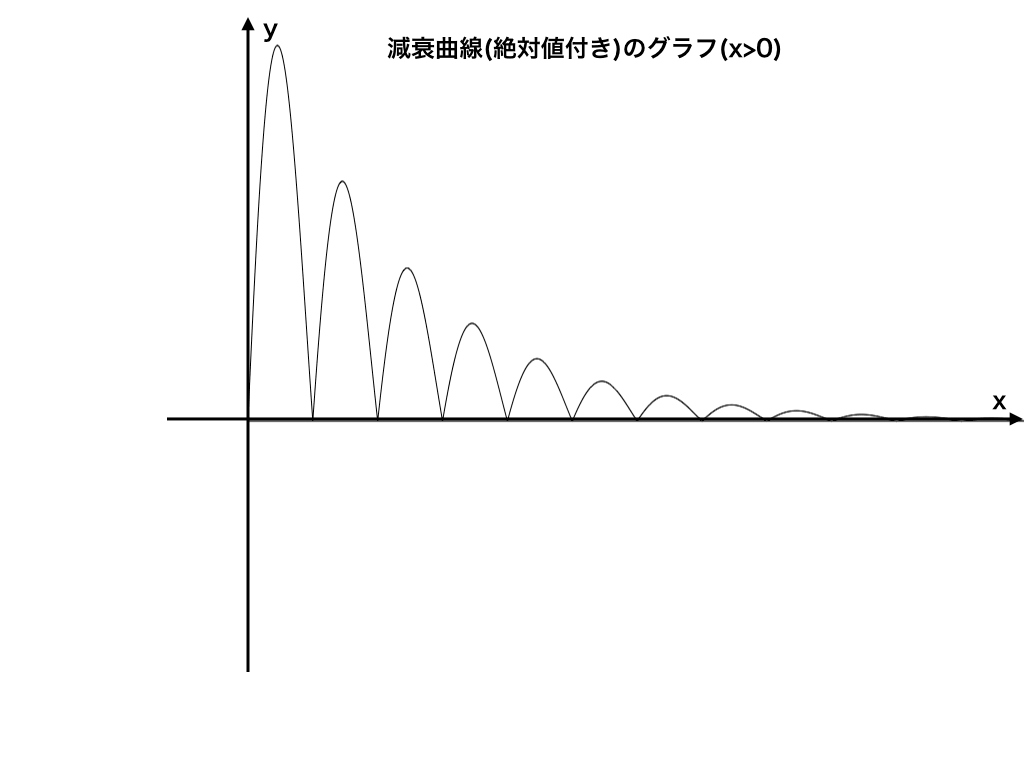
<図2:絶対値付きの減衰曲線の関数のグラフ>
解答とその流れ
まず、以下の<図3>のように3つの段階を経てときます。
stepⅠ:1つ分の面積を(数列)の式であらわし→
stepⅡ:その数列の1からnまでの総和Snを求め→
stepⅢ:最終的にその極限を計算します。
(※:下図右の②は\(\sum_{k=1}^{n}a_{k}\)です。)
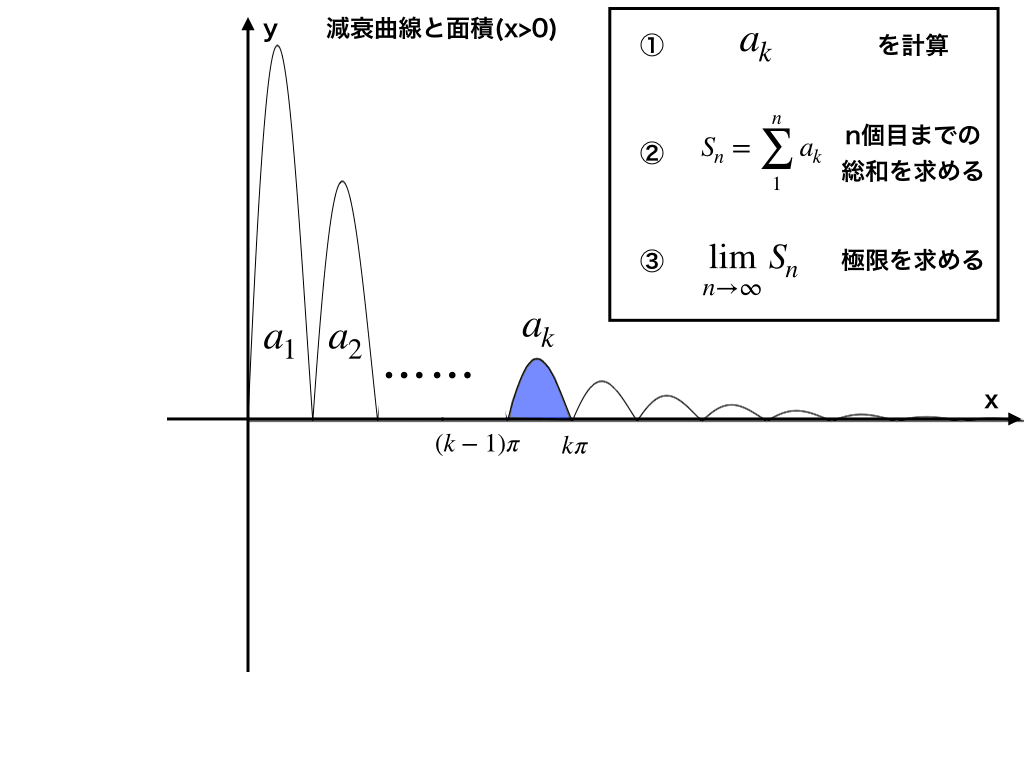
<図3:求積の手順>
step1:一つ分\(a_{k}\)山一個分の面積を求める
まず始めにk番目の面積(図3の青色で塗ってある部分):これを\(a_{k}とする\)を求めていきます。
$$a_{k}=\int_{(k-1)\pi}^{k\pi}e^{-x}|\sin x| dx$$・・・(式1)
置換積分のコツ
上の式を計算すればakが求まりますが、積分区間に”k"、"k-1"が混ざっています。
このような時は、積分区間がきれいになるように新たに文字を置くことが重要です。
ここでは、\(u=x-(k-1)\pi \)という関係を満たす文字"u"を使います。
※:こんな文字の置き換えは思いつかない!という人は「複雑な範囲が、”0”や”π”になるにはどうすればいいか?」を考えてみると良いです。
uで置き換え
\(u=x-(k-1)\pi \)より、\(x=u+(k-1)\pi\)なので、(式1)のxに代入し、$$\frac{du}{dx}=1$$なので、uで置換すると
$$a_{k}=\int_{0}^{\pi}e^{-(u+(k-1)\pi)}|\sin (u+(k-1)\pi)|du$$
\(\sin (u+\pi)=\sin u \)「三角関数の還元公式(θ+90°),(θ±π)など」かつ、\(0→\pi \)においてサインは常に0以上なので、絶対値を外すことができます。
さらに、eの指数部分の内"u"に関係のない部分は前に出せるので、
$$a_{k}=e^{-\pi(k-1)}\int_{0}^{\pi}e^{-u}\sin u du$$
ここで、上の定積分を行います。
(指数)×(三角関数)の積分のコツ【ペアを作れ!】
指数関数×三角関数 の積分は、もちろん部分積分を用いても可能ですが、『ペアを作って→足したり引いたりする』ことによって楽に求めることができます。(「和積や積和の公式を作る時」と似ています。)
具体的に\(e^{-u}\sin u\)の積分を行うときは、
\(A=e^{-u}\sin u \)と\(B=e^{-u}\cos u \)として、A,Bをそれぞれ微分し、
\(A'=-e^{-u}\sin u+e^{-u}\cos u\)
\(B'=-e^{-u}\cos u-e^{-u}\sin u\)
A'+B'をした上で両辺を2で割り、
\(A'+B'=(A+B)'=-2e^{-u}\sin u\)
両辺を積分することで、
$$ -\frac{(A+B)}{2}=\int e^{-u}\sin u dx$$
と求めることができます。
したがって、$$e^{-(k-1)\pi}[-\frac{e^{-u}(\sin u +\cos u)}{2}]_{0}^{\pi}$$
これを計算すると、$$a_{k}=(\frac{-e^{\pi}+1}{2})\times e^{-(k-1)\pi}$$
stepⅡ:\(a_{1}\)から\(a_{n}\)までの総和を求める
次に、\(a_{k}\)をよくみると、\(e^{-(k-1)\pi}\)の部分が初項1、公比\(e^{-\pi}\)の等比数列になっていることがわかります。
そこで、k=1からnまでの和を求めると
$$S_{n}=\sum_{k=1}^{n}a_{k}$$
$$\frac{-e^{\pi}+1}{2}\cdot \sum_{k=1}^{n}(e^{-\pi})^{k-1}$$
「等比数列の和の公式」より、
$$S_{n}=\frac{(1+e^{-\pi})(1-(e^{-\pi})^{n})}{2-2e^{-\pi}}$$
・・・これがstepⅡの答えです。
stepⅢ:Snの極限をとる
いよいよラストです。部分和Snのnを∞にすることで、全ての面積を求めることができます。
\(\lim_{n\rightarrow\infty}Sn\)
において、\((e^{-\pi})^{n}\)の部分は0に収束し、
最終的に残るのは、$$\frac{1+e^{-\pi}}{2-2e^{-\pi}}=\frac{e^{\pi}+1}{2e^{\pi}-2}$$
なので、\(y=e^{-x}|\sin x|\)とx軸で囲まれた部分の面積は$$\frac{e^{\pi}+1}{2e^{\pi}-2}$$
・・・が答です。
減衰曲線と面積まとめ
このレベルの問題になってくると、計算や置換積分などに工夫が必要で、ミスもしやすくなります。
解法の3stepを理解したら、繰り返し自分で問題を解いて、【素早く・正確】に答えまでたどり着ける様に頑張りましょう!
関連記事(微積分/極限)一覧
\\「数学Ⅲ:微分積分とその応用まとめページ」//
\\「極限の解説記事8選まとめ」//
今回も最後までご覧いただき、ありがとうございました。
【受験/学習メディア】:「スマホで学ぶサイト、【スマナビング!】」では,コメント欄にて、読者の皆さんのご感想を募集しています。
(※:”個別の問題の質問”等には、対応出来ない事があります。)
・その他の【お問い合わせ・ご依頼・タイアップ】などに付きましては、【運営元ページ】よりご連絡をお願いします。

