偏微分とは?全微分/合成関数の微分と合わせてわかりやすく解説

高校数学ではじめる機械学習シリーズ(2)

・この記事では、機械学習への応用を視野に入れつつ『偏微分』・『合成関数の微分』・『全微分』を解説しています。

（・前回からご覧くださっている方へ）：「回帰分析とは？その意味と勾配降下法（上）」に引き続いて、目的関数を最小化する方法である、『勾配（最急）降下法』を理解するために必要な、”偏微分”・”合成関数の微分（連鎖律）”を紹介していきます。

単回帰分析(1)の復習

前回は、勉強時間とその後のテストの関係という１変数での予測方法として、一次関数でモデル化する（これを『単』回帰分析と呼びました）ことを学習しました。

目的関数の復習

その際に実際のデータとの誤差を”目的関数”を使って計算することを学びました。

＜目的関数の式＞

$$J(β)=\frac {1}{2}\sum ^{n}_{i=1}\{ y^{(i)} -h_{β} ( x^{(i)}) \} ^{2}$$

偏微分とは？勾配降下法の準備

さらに、この目的関数を最小化するために『勾配降下法』という方法を用いてみる、というところまでが第1回の内容でした。

この項では、実際にその『勾配降下法』を利用するにあたって必要な、『偏微分』・『合成関数の微分法』を高校数学の記事とリンクさせながら、紹介していきます。

高校2年・3年で習う微積分 (準備)

偏微分（大学で習う範囲です）の前に、高校で初めに習う１変数関数（f（x）＝x2＋３x−1 など）の微分について、不安がある方は、以下の記事でそれぞれ解説しています。

「三次関数の微分とグラフ(高2)」

「微分法のまとめ記事」

「微分の基礎・微分係数と導関数の違い」

また、”偏微分が可能な条件”について知識が必要になった時のために、１変数関数の微分可能条件を先に頭に入れておきましょう。

「関数の連続と微分可能の意味（数学３・極限/微分法)」

偏微分は多変数関数のある一つの変数を微分する

上の通りで、本シリーズでは偏微分に関してはこれくらいの理解で良いかと思います。

とは言っても、具体的にどのような計算をするのか見てみないと実感がわかないかと思うので、２変数関数を使って、実際に偏微分をしてみます。

２変数関数での偏微分と用語の紹介

これまでの１変数関数の微分では、d/dx という記号を用いて微分を表していましたが、偏微分では”d”の代わりに"∂"という記号（ラウンドと呼びます）を使用します。

f(x,y)=2x²+3xy+3y²+2y+1 ・・・★この関数を例に偏微分をしてみましょう

$$\frac {∂f(x,y)}{∂x}=(2x^{2})'+3(x)'y=4x+3y$$

上の式のように、xでf(x,y)を偏微分した場合、xのみ微分し、x以外を定数として扱います。

つまり、３xyでは(3y)はxの係数とし、xが付いていない”3y²”、"2y"、"1"はそれぞれ定数項として微分されて消えています。

g(x)=2x+1 という１変数関数を微分すると、定数項の”１”が消えてg'(x)=2となることと同じです。

次に、同じf(x,y)をyで偏微分してみます。

$$\frac {∂f(x,y)}{∂y}=3x(y)'+(3y^{2})'+(2y)'=3x+6y+2$$

この場合は、y以外の2x²と１は定数項として微分されて消えています。

このように、偏微分という名前はいかにも難しそうですが、基本的には高校レベルの微分とほとんど難易度は変わらないことがわかって頂けたのではないでしょうか？

2変数関数での全微分

偏微分と全微分

この際なので、”偏微分”とともに”全微分”についても軽く紹介しておきましょう。

２変数関数での偏微分を以下のようにして足し合わせたものを”全微分”と呼びます。

全微分の計算方法

$$df=\frac {\partial f}{\partial x}dx＋\frac {\partial f}{\partial y}dy$$

f(x,y)=2x²+3xy+3y²+2y+1 ・・・★の式で、全微分してみましょう。

df=(4x+3y)dx+(3x+6y+2)dy

この全微分のイメージは、接平面です。１変数関数での微分は、傾きを表しました。

＜参考＞２変数関数をx-y-zの３次元空間で表すと以下の図のようになります。

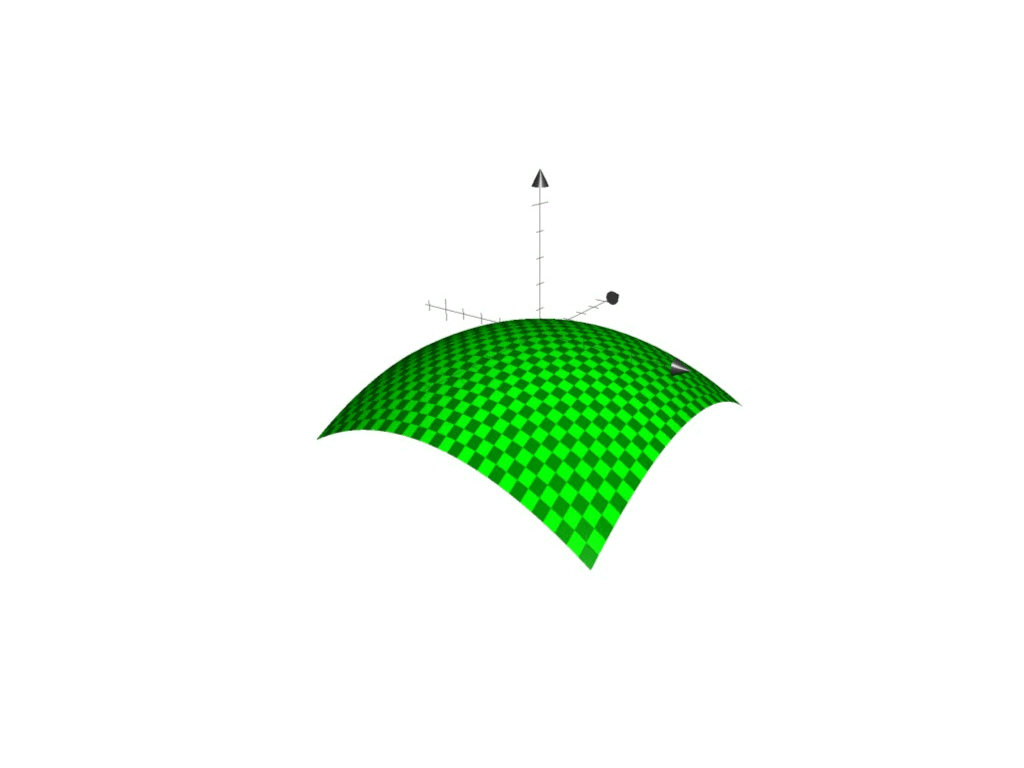
＜２変数関数のイメージ＞

接線と接平面・全微分の関係

なお、『接平面』に関しては高校数学B：空間ベクトルのところで解説しているので、そちらも是非あわせてご覧ください。

＞＞「曲面の方程式と接平面を解説（空間ベクトルの応用）」＜＜

合成関数の微分(チェーンルール)

第二回の最後に、目的関数を偏微分するときに”合成関数の微分”という考え方を用います。

これが少しややこしいので、この項でなるべく簡単に紹介しておきます。

（詳しくは→「合成関数微分と対数微分法の仕方」の合成関数〜のところをご覧ください）

合成関数とは、関数の中に関数が入っているイメージです。

そして、微分の記号"dy/dx"をあたかも分数のように扱って、なるべく楽に微分するのが合成関数の微分法です。

例)dy/dx＝dt/dx・dy/dt

勾配降下法では、目的関数$$J(β)=\frac {1}{2}\sum ^{n}_{i=1}\{ y^{(i)} -h_{β} ( x^{(i)}) \} ^{2}$$の中にさらにhβ（x）が入っているので、まず全体をhβ(x)で微分します。

次にhβ(x)をβ0で微分し、それぞれをかけ合わせることによって、目的関数を直接βで微分したことと同じ結果が得られます。（具体的には次回説明します。）

$$\frac {∂J(β)}{∂β_{0}}=\frac{∂J(\beta )}{∂h_{\beta}(x)}\cdot \frac{∂h_{\beta}(x)}{∂β_{0}}$$

偏微分まとめと次回:最急(勾配)降下法の具体的なやり方へ

・偏微分は多変数関数のうち一つの変数に注目して微分するものである。

・勾配降下法においては、目的関数のパラメーターを最適化するために偏微分を利用する。

・合成関数の微分は、関数の中に関数が入っているような場合に用いる

次回は、勾配降下法を今回学んだ偏微分を利用して解説し、目的関数（データとの誤差）を最小化する方法をまとめて解説します。

高校数学レベルから始める機械学習シリーズ

数学知識編（未定乗数法の記事を追加しました。2020/02/19）

第3回を追加しました。

・第0回：「機械学習のための数学の知識記事一覧」

・第1回：「単回帰分析の意味と目的関数」

・第2回：「今ここです」

・第3回：「勾配降下法（下）の仕組みと手順をイラストで解説」

・第4回：「重回帰分析とは何か？（製作中です）」

＞「ラグランジュの未定乗数法について」：今回学んだ偏微分を用いて、『ある条件のもとでの最大値の候補』を見つけ出す、大変有効な手法です。

最後までご覧いただき有難うございました。

当サイトは皆さんの記事リクエストやご質問・ご意見をお待ちしています。

ぜひコメント欄までお寄せください。

snsでシェア、B!や、Twitterのフォローをしていただけると嬉しいです。