
こんなに使える!:1/6・1/3公式(数2積分法)
<この記事の対象>:1/6,1/3公式を知らない人〜知っていてもどう使えば良いか”コツ”がつかめない「数学2」の積分を学んでいる人。
<この記事の内容>:主に”裏ワザ”的に紹介される"1/6","1/3"公式の基本を紹介した後、入試などではそのまま(直接)使える例はそこまで多くないことから、工夫して”6分の1”が使える形にする方法などを解説しました。
目次(タップした所へ飛びます)
1/6公式と関連する公式【理解/基礎編】
大抵の人はこれから紹介する式(+その派生型)をどこかで目にしたことがあると思います。
この項では、その中でも使用頻度が高いものを図解し、定着用の例題で基礎を固めます。
1/6や1/3公式をイラストで理解する
イラストを交えて、最頻出+重要な4つのtypeを紹介していきます。
直線と放物線(二次関数)type1
最も重要で、全ての基本となるタイプです。
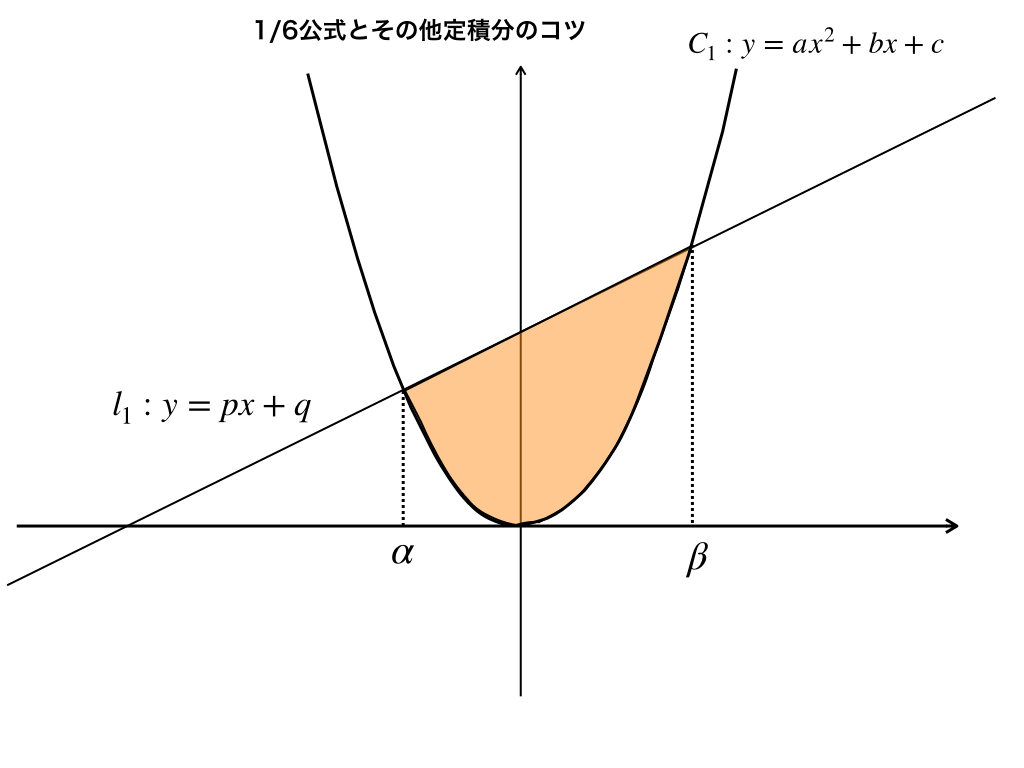
放物線\(C_{1}:y=ax^{2}+bx+c\)と、\(直線l_{1}:y=px+q\)の交点のx座標を\(\alphaと\beta\)とした時、<図1>中の\(C_{1}とl_{1}\)に囲まれた面積は$$\frac{a}{6}(\beta-\alpha)^{3}$$
さらに、<図1>は下に凸の放物線でしたが、上に凸の場合でも成り立つように、$$\frac{|a|}{6}(\beta-\alpha)^{3}$$と絶対値をつけておきます。
(いわゆる『6分の1』になるのは、放物線の式中の\(x^{2}\)の係数:a=1の場合です。)
この公式のpointは、\(C_{1}とl_{1}\)を連立して求めた解(交点)がわかれば、曲線の二次の係数\(aと(2つの解の差)^{3}\)で求まる点です。
(マーク式などでは無い、記述が必要な場合には、途中まで積分の式を書くようにしておきましょう。)ex:$$\int^{\beta}_{\alpha}(px-q)-(ax^{2}+bx+c)dx$$
$$=-a\int^{\beta}_{\alpha}(x-\alpha)(x-\beta)dx$$
放物線同士が囲む面積:type2
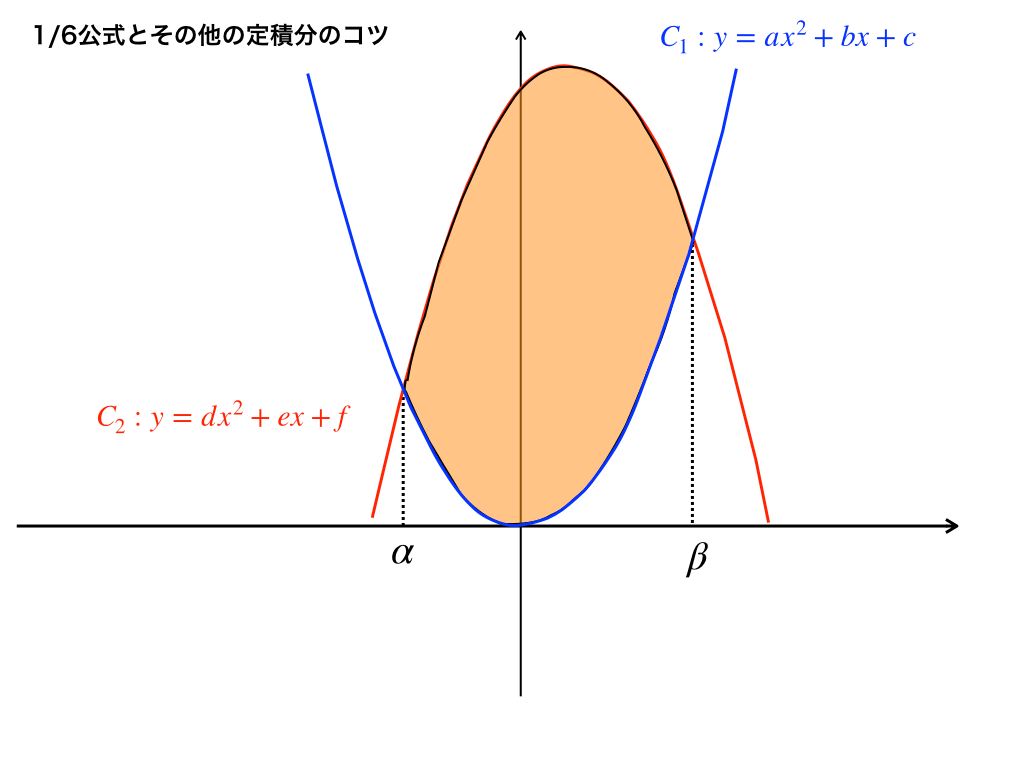
<図2>のように放物線が”二つ”になると、その間の面積は、$$\frac{|a-d|}{6}(\beta-\alpha)^{3}$$絶対値の中身が【2つの放物線の二次の係数の差】になり、分母が『6』で変化ありません。
放物線とその接線・x=()で囲まれた部分の面積:type3
次は「3分の1公式」のタイプです。
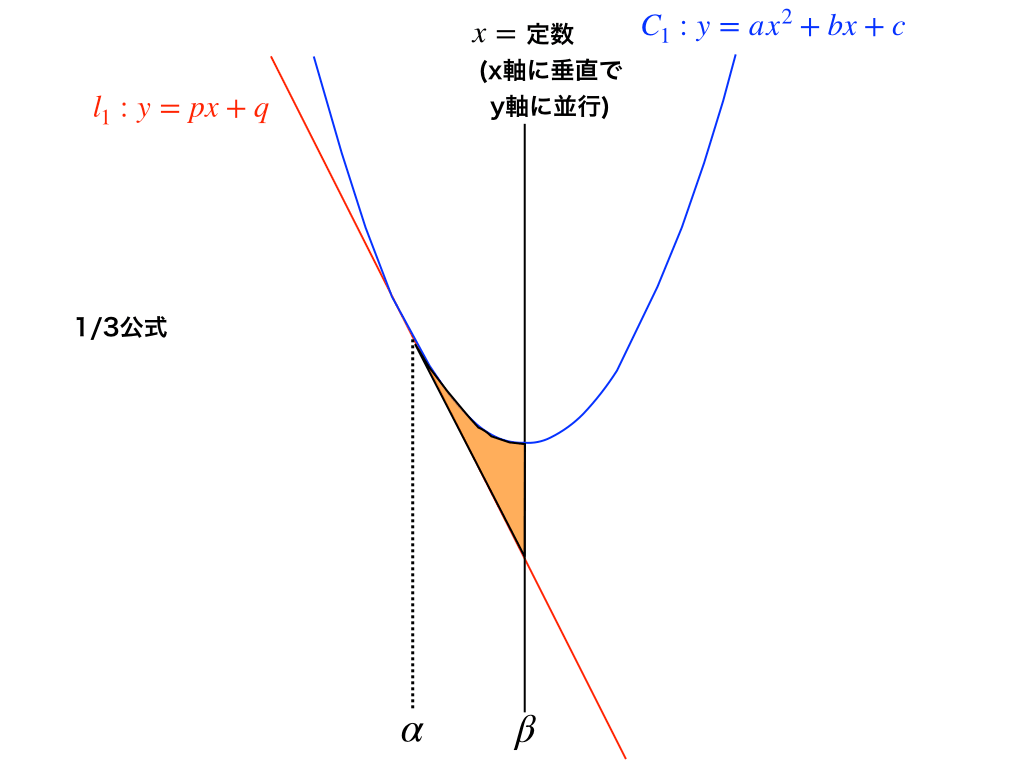
<図3>のように、x=0(=y軸)などのx軸に垂直な直線と、放物線・その接線の三つに囲まれた面積は$$\frac{|a|}{3}(\beta-\alpha)^{3}$$で求める事が出来ます。
このtype3はtype1や次のtype4と同じくらい頻繁に使うことになるのでチェックしておきましょう。
二次関数のグラフの接線2つ:type4
このtype4は、特に強力な道具になるので何度か問題演習をしておきたいものです。
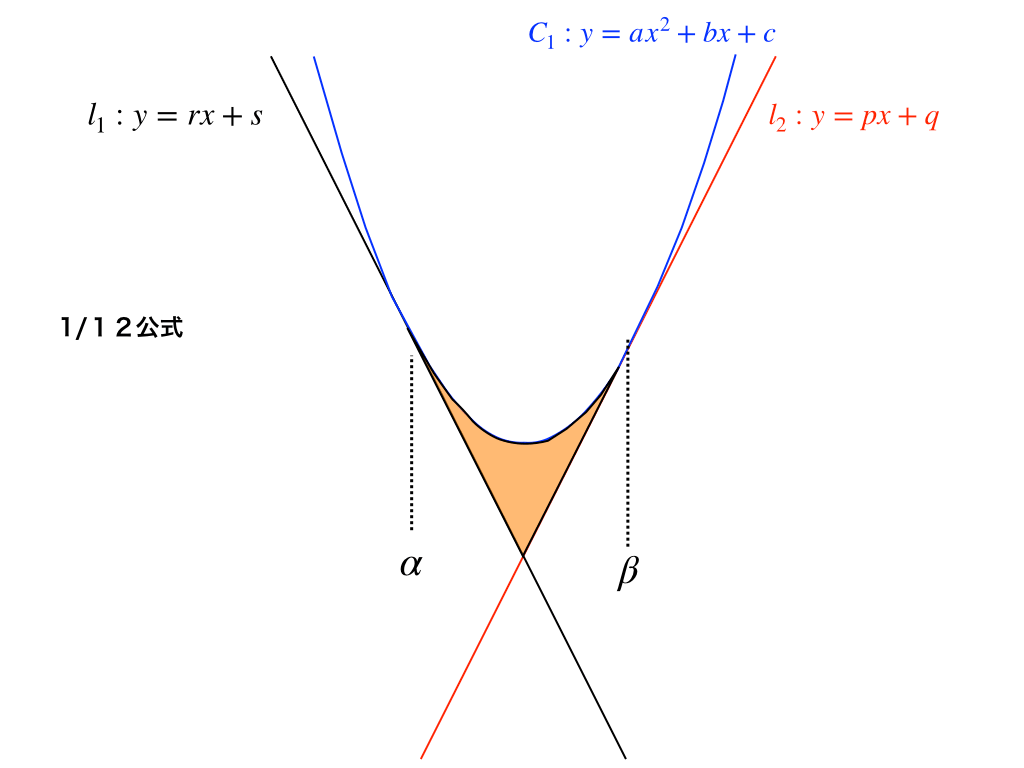
<図4>の放物線\(C_{1}\)とその接線2つ:\(l_{1}、l_{2}\)で囲まれている部分の面積は$$\frac{|a|}{12}(\beta-\alpha)^{3}$$
1/6を求積問題で使うコツ【実践編】
さて、上の【理解・基本公式編】では主な公式とその使用法を確認しました。
ここからは、一段階レベルアップした工夫しないと公式が使えないタイプを紹介していきます。
直接使える問題は減っている!
非常に便利な「6分の1や3分の1、12分の1」公式ですが、実際の入試では簡単に使わせない様にうまくカモフラージュされている事が普通です。
(この”裏”ワザが広く知れ渡って、もはや”表”ワザの様になっているため、そのままの形で出題しても差がつきません)
ではこれらの公式は必要ないのかというと、もちろんそんなことは無く、
・パズルを解くように公式が使える形に”分割”したり、
・複数回利用して、あえて余分な部分を計算する
・三角形などの”有名な図形の面積公式”と組み合わせる
などなど、、の”図形的な工夫”をすることで十分に通用します。以下の問題で実際にその”工夫の仕方”を紹介します。
面積を求める問題
以下の図のように、2つの放物線\(C_{1}:y=2x^{2}+2x\)、\(,C_{2}:y=x^{2}-1\)と、
その接点を通る\(直線l_{1}:y=2x+2\)が存在する。
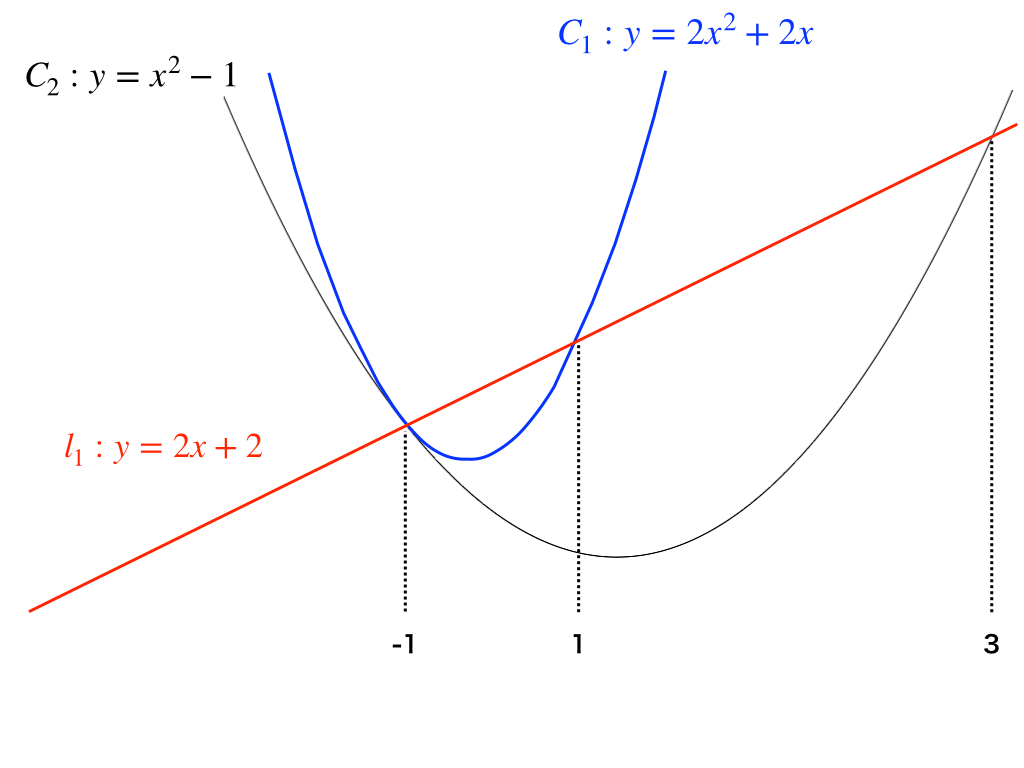
このとき、\(C_{1},C_{2}、と、l_{1}\)で囲まれている部分の面積を求めよ。
解答解説(求積編)
さて、この問題を普通に解くと、\(l_{1}がC_{1}\)の上にあるところで、\(C_{1}とC_{2}\)の間の部分の面積を求め・・・step1
次に\(l_{1}とC_{2}\)の間の部分の面積を計算し・・・step2
さらにその上で、step 1と2で求めたそれぞれの面積を足し合わせることになります。
この方針で計算を進めると、1/6、1/3、1/12のいずれの公式も使えないので非常に面倒+ミスの危険が増えます。
図形のパズルを解いて公式が利用できる型へ
そこで、まずはじめに\(C_{2}とl_{1}\)が囲む面積を求めます。これはおなじみの1/6公式が使えますね!
$$\frac{|1|}{6}(3-(-1))^{3}$$・・・(一)
次に、不要な部分を削ってしまいます。(先ほど挙げた《余分な部分》を計算しているからです)
ここでは\(C_{1}とl_{1}\)が囲む部分の面積がそれに当たります。この余分な面積も1/6公式です。
$$\frac{|2|}{6}(1-(-1))^{3}$$・・・(二)
従って、(一)ー(二)で答えが求まります。
$$=\frac{64}{6}-\frac{8}{3} ∴ 8$$
ぜひ一度普通の積分計算もしてみて、計算量の差を実感してみてください!
まとめと続編へ
今回は基本中の基本であるtypeを紹介しましたが、そのほかにも何種類か派生したタイプが存在します。(2019/10/03現在:作成中です)
とにかく基礎を抑えて、工夫する方法を学べば効果は非常に高いことに変わりありません。
特に数学2の求積問題に取り組むときは、常に”上手く”これらの公式に帰着できないかを『頭の片隅に置いて』解いていく様にしましょう。
微分・積分と関連分野の記事一覧
学習・受験対策メディア:スマホで学ぶサイト『スマナビング!』では読者の方からの、ご意見・ご感想をコメント欄で募集しています。
(※):ただ今、個々の問題のご質問については対応できない場合があります。
(誤植の指摘や、ご感想は引き続き募集しています。)
・お問い合わせ/ご依頼等、その他のご連絡については、【運営元ページ】よりお願いいたします。(こちらは通常通り受け付けています。)

