
積分漸化式の基本(一)
<この記事の内容>:積分法の応用でも、式が複雑で難しそうな「積分漸化式」の意味と使い方、定積分を変形をして【問題で与えられた漸化式のカタチ】にする方法を解説しています。
<関係する記事>:「”微分積分”とその応用分野の記事まとめ」
目次(タップした所へ飛びます)
積分漸化式とは?
その名の通り、『積分』のカタチ(例:\(\int_{1}^{e}\log^{n}{x}\))で表された『漸化式』(そのままです)のことです。『漸化式の詳しい意味』は左の記事の冒頭で解説しています。
この類の問題は、一度やっておかないとテストなどで解きづらいタイプなので、解法をこの記事で学んだら『自力で』関係式を導けるようになるまで練習をしておきましょう。
初めの(基本的な形)であるサイン型は、なるべく式変形を省略せず解説していきます。
sin(正弦)の積分漸化式の問題
早速、サインについて見ていきます。
$$I_{n}=\int_{0}^{\frac{\pi}{2}}\sin^{n}x dx$$ とする時、\(I_{n}とI_{n-2}\)の漸化式を導き・・・(1)
$$\int_{0}^{\frac{\pi}{2}}\sin^{4}x dx$$ の値を求めよ。・・・(2)
解法と使い方
まずは今回のメイン:(1)を解いていきましょう。
関係式を作る
問題文が??な人もいるかもしれませんが、数列の場合と同じく、『\(I_{n}\)の式を変形して、\(I_{n}=○I_{n-2}\)のカタチにせよ』ということを言っています。
\(I_{n}=\int_{0}^{\frac{\pi}{2}}\sin x\sin^{n-1}x dx\)
↑最大のポイントです。sinのn乗をsinの”1乗”と”n-1乗”に分けて(積の形にして)、部分積分を行います。
「部分積分の復習はこちら」の記事をご覧ください。
(上の記事中の方法を用いて、次のように微分・積分される関数を決めます。)
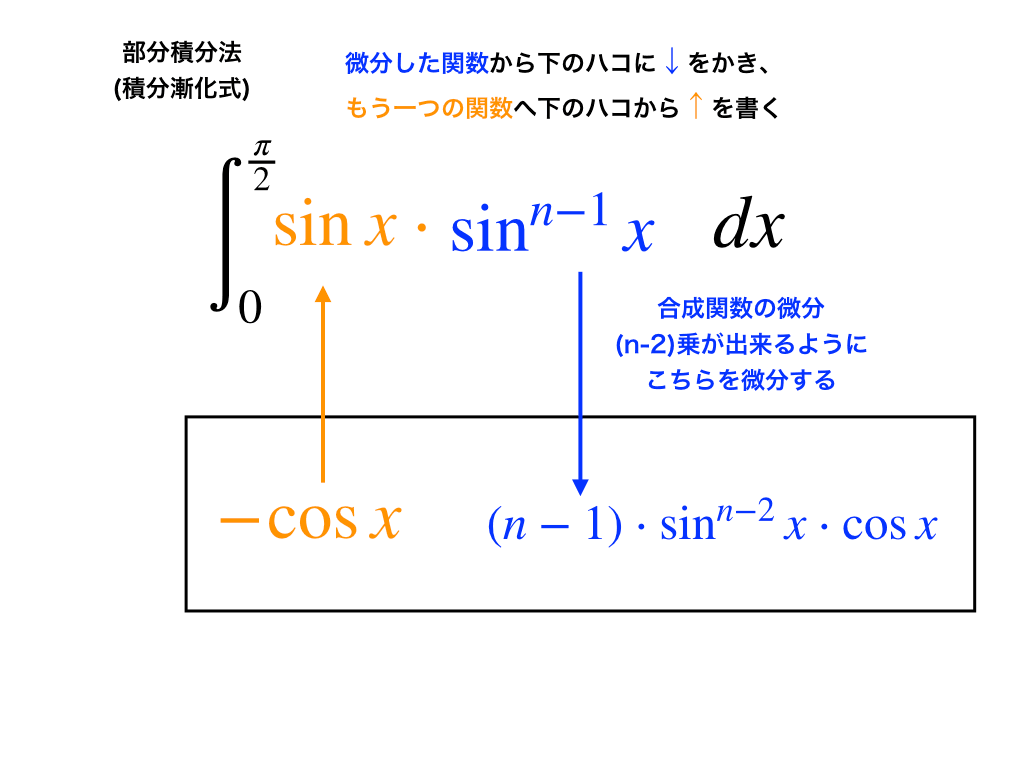
オレンジの矢印の根元の”コサイン”と、青の矢印の根元にある”サインのn-1乗”を、そのまま定積分の【】に入れます。
次に、下の箱に入った関数を掛け合わせて\(\int dx\)の中に組み込みます。
$$=[-\cos x\sin^{n-1}x]_{0}^{\frac{\pi}{2}}+\int_{0}^{\frac{\pi}{2}}(n-1)\cos^{2}x\sin^{n-2}x dx$$
ここで、前半部分はcosとsinの積になっており、『2分のπ』・『0』のそれぞれを入れた時、ともに0になるので後ろの定積分のみ残ります。
三角比(関数)の相互関係より、\(\sin^{2}+\cos^{2}=1\)を使って、
\(=(n-1)\int_{0}^{\frac{\pi}{2}}(1-\sin^{2}x)\sin^{n-2}x dx\)
展開して、
\(=(n-1)\int_{0}^{\frac{\pi}{2}}\sin^{n-2}x-\sin^{n} dx\)
この定積分を2つに分けた上で、\(=I_{n}\)であることから、
$$I_{n}=(n-1)\int_{0}^{\frac{\pi}{2}}\sin^{n-2}x dx-\int_{0}^{\frac{\pi}{2}}\sin^{n}x dx$$
よって、この式はIn,In-2を使って、
\(I_{n}=(n-1)(I_{n-2}-I_{n})\)と表すことができるので、これを整理すると
$$I_{n}=\frac{n-1}{n}I_{n-2}$$
・・・(答)
漸化式を”使う”
さて、次はn乗の部分が”4”という具体的な数字の時を、上で導いた漸化式を用いて計算します。
(2)を(1)で使ったInで表すと『\(I_{4}\) を求めよ』と言われているので、まず\(I_{2}\)を計算した上で\(I_{n}とI_{n-2}\)の関係を使います。
\(I_{2}=\int_{0}^{\frac{\pi}{2}}\sin^{2}dx\)
\(=\frac{\pi}{4}で、I_{n}=\frac{n-1}{n}I_{n-2}\)のnに4を代入すると\(I_{4}=\frac{3}{4}I_{2}\)
となるので、I2をこの式に再び代入して、\(I_{4}=\frac{3}{4}\times\frac{\pi}{4}=\frac{3\pi}{16}\)
さまざまな関数の積分漸化式
さて、積分漸化式には正弦(sin)以外にも色々な関数を題材にしたものがあります。
ここでは、その中でも特に頻出&次回以降に解説する『メルカトール・ライプニッツ級数』や『ウォリスの公式』など、応用問題と絡めて出題される”3つの関数”についてサインの時と同様に紹介していきます。
cos(余弦)バージョン
$$I_{n}=\int_{0}^{\frac{\pi}{2}}\cos^{n}x dx$$ とする時、\(I_{n}とI_{n-2}\)の漸化式を導け。
cosバージョンは、sinの時とやることがほとんど同じなので、できれば自分でやって見てください。
以下(答)の変形です。
cos×cosのn-1乗を行い、\(\sin^{2}x=1-\cos^{2}x\)を用いて
\(I_{n}=[\sin x\cos^{n-1}x]_{0}^{\frac{\pi}{2}}+(n-1)\int_{0}^{\frac{\pi}{2}}\sin^{2}x\cos^{n-2}x\)
前半の定積分は0になるので、
$$I_{n}=(n-1)\int_{0}^{\frac{\pi}{2}}\cos^{n-2}x-\cos^{n}x dx$$
\(I_{n}=(n-1)(I_{n-2}-I_{n})\)
これを整理することで、\(I_{n}=\frac{(n-1)}{n}I_{n-2}\)・・・(答)
tan(正接)バージョン【コツ1】
$$I_{n}=\int_{0}^{\frac{\pi}{4}}\tan^{n}x dx$$ とする時、\(I_{n}とI_{n-2}\)の漸化式を導け。
タンジェントの場合は、
・積分区間が違うこと
・式変形がsin,cos型と異なること
から、初見では少し難しい?かもしれません。
hintとしては、「三角比の相互関係」の中の\(1+\tan^{2}x=\frac{1}{\cos^{2}x}\)を利用します。
2乗のくくりだしと三角比の相互関係
まず、\(\int と dx\)の間で、\(\tan^{2}x\tan^{n-2}x\)を作り、
\((\cos^{2}x-1)\cdot\tan^{n-2}x=\frac{\tan^{n-2}x}{\cos^{2}x}-\tan^{n-2}x \)にします。
それぞれを積分すると、$$I_{n}=[\frac{\tan^{n-1}x}{(n-1)}]_{0}^{\frac{\pi}{4}}-I_{n-2}$$
よって、\(I_{n}=\frac{1}{n-1}-I_{n-2}\)・・・(答)
log(対数関数)バージョン【コツ2】
$$I_{n}=\int_{1}^{e}\log{x} dx$$ とする時、\(I_{n}とI_{n-1}\)の漸化式を導け。
対数関数の部分積分ではおなじみの、\(\int 1\cdot \log{x}dx\)(《1》をログの前に作る)方法を用います。
”1”×logを作って部分積分
$$I_{n}=[x(\log{x})^{n}]_{1}^{e}-n\int_{1}^{e}(\log x)^{n-1}dx$$
[カッコ]内の部分は計算すると=eとなり、定積分の部分は\(nI_{n-1}\)と書けるので\(I_{n}=e-n\cdot I_{n-1}\)・・・(答)
まとめと応用編へ
今回は式が多く、一回で習得するのは難しいかもしれません。
ただ、上述した様に積分漸化式はさらなる応用問題の基礎になっていることも多いので、ぜひなんどもこの記事を読んで定着させてください!(特に、難関大・単科医大を目指す人は必須です。)
関連記事と続編
「(応用編を作成中です)」
ライプニッツ級数 とメルカトル級数etc、、、
今回も最後までご覧いただき、有難うございました。
お役に立ちましたら、SNS等でシェアして頂けると幸いです!
【受験メディア】:「スマホで学ぶサイト、『スマナビング!』」では、コメント欄にて読者の方のご感想を募集中です。(※:現在、個々の問題の質問には返信出来ない場合がございます。)
・その他のお問い合わせや、ご依頼、スマナビング!とのタイアップなどに付きましては、【運営元ページ】よりご連絡をお待ちしています。

