y軸回転体の体積の求め方とバウムクーヘン分割の使い方

2019-10-23 2019-10-23

当サイトを執筆した講師陣による個別指導を受けてみませんか？

【大学受験・英検・TOEIC・数検をはじめとする各種検定/資格試験の合格・スコアアップ】を達成するYESのマンツーマン指導。体験授業随時受付中！

個別指導塾YES

数学Ⅲ：体積其の二（y軸回転体）

＜この記事の内容＞：「積分法の応用：体積の求め方(一)」に引き続き、今回は【y軸を中心として一回転した物体】の

・基本的な求積パターン(前半で解説)と

記事後半で同じ問題を

・《バームクーヘン(分割)積分》を用いて解く方法を紹介しました。

※：三角関数の変形公式などは、必須(忘れたり、知らなければその時点で1題丸々失点します)なので、

・「三角関数の公式を覚えず導く方法のまとめページ」で【苦手な公式をその場で作る】練習をしておきましょう！

目次(タップした所へ飛びます)

y軸に関する回転体2通りの求積法
- 基本パターンと例題
- 具体的な手順と解答・解説
バウムクーヘン分割の応用
まとめと次回予告
- 関連記事一覧(数学Ⅲ)

y軸に関する回転体2通りの求積法

上述したように、まずは基本となる求積パターンをこの項で見ていきます。

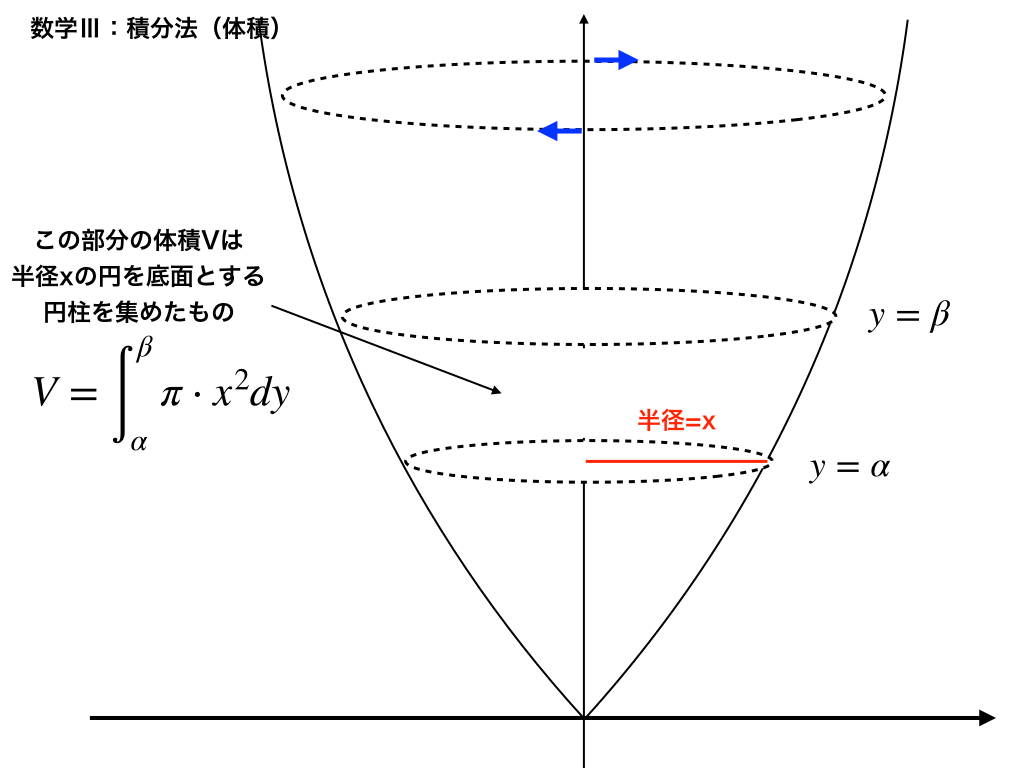
基本パターンと例題

例題1：$y＝\cos x $とx軸$y＝0、および、y軸：x＝0$で囲まれた部分をSとする。Sをy軸に関して一回転させた時にできる物体の体積を求めよ。

具体的な手順と解答・解説

step by stepで解いていきましょう。

step 1:xに直接代入できるかチェック

$$\int^{1}_{0}\pi x^{2}dy$$

$y=\cos x $より、x=のカタチにして代入するのは難しいです。

step 2:無理ならば置換積分を行う

そこで、置換積分→「置換積分法の解説と手順・パターンまとめ」を用い(dy/dx)を分数の“ようなもの”として扱って、次のstep2-2のようにxだけの積分のカタチに変形します。

step 2-2：”dx”の部分と”積分区間”に注意して式変形

まずは、$\frac{dy}{dx}dx$の部分で帳尻を合わせて、積分区間が

・y＝0の時x=π/2

・y＝1の時x＝0

なので、

$$\int^{0}_{\frac{\pi}{2}}\pi x^{2}\frac{dy}{dx}dx$$

step3：”dy/dx”を計算し”x”で積分

さらに、$dy/dx=-\sin x$より

$$\pi\int^{0}_{\frac{\pi}{2}} x^{2}(-\sin x) dx$$

上の式を積分すると問題の体積が求まります。

ただし、計算が煩雑になる(参照：「部分積分の手順と楽に解くコツ(下箱法)」)ので、注意が必要です。

1回目の部分積分は、xの二乗を微分する側・sinx を微分される側として

$$\pi[x^{2}(-\cos x)]^{\frac{\pi}{2}}_{0}+\pi\int^{\frac{\pi}{2}}_{0}2x\cos x dx$$

2回目は、2xを微分する側・cos x を微分される側とし

$$\pi[x^{2}(-\cos x)]^{\frac{\pi}{2}}_{0}+\pi[2x\sin x]^{\frac{\pi}{2}}_{0}-2\pi[-\cos x]^{\frac{\pi}{2}}_{0}$$

結果的に、$π^{2}-2π$・・・（答）

バウムクーヘン分割の応用

さて、上のcos x の回転体を見方を変えて、もう少し楽な【バウムクーヘン積分(年輪法、などいろいろな名前があります)】を解説していきます。

バウムクーヘンor年輪法とは何か

以下のイメージのように、回転した円形の部分から、微小な厚み(dx)を持つ立体を切り出して、真っ直ぐに伸ばすと【直方体】ができます。

イメージ

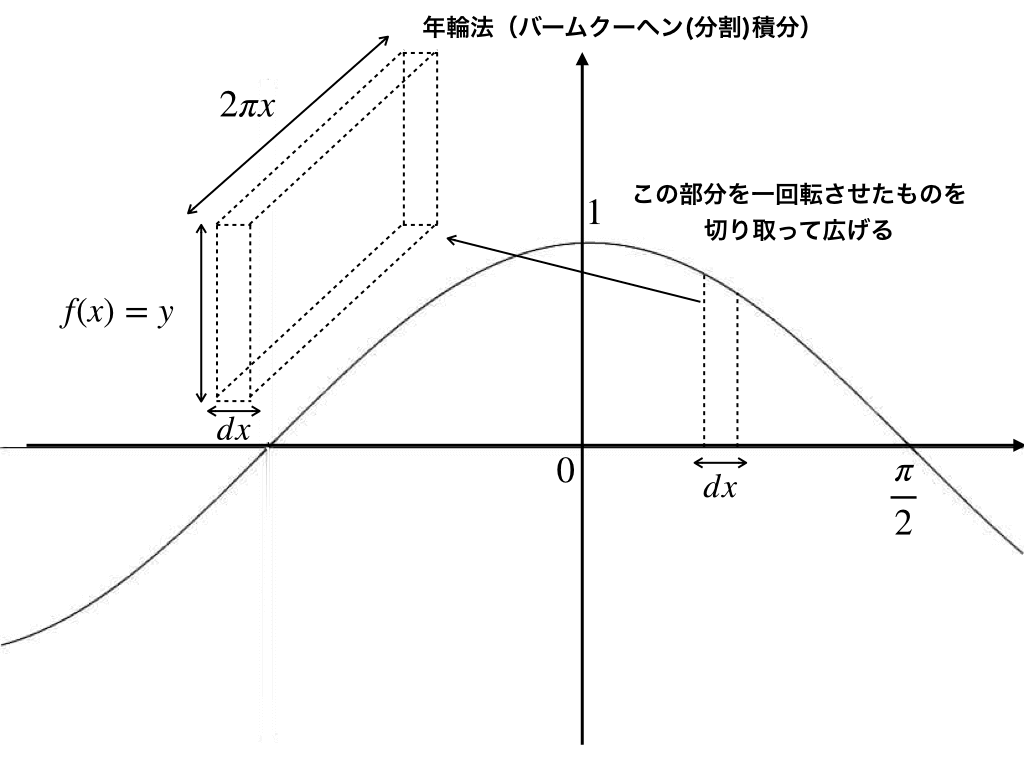
これを対応する【xの積分区間で定積分】することによって、初めのパターンの体積を求めることができます。

例題で定着

例題2：例題1と同じ《S》をy軸まわりに回転させた場合の体積を、年輪法(orバームクーヘン積分)で求めよ。

解答解説

step 1:切り出す直方体の情報をまとめる

直方体の情報を整理して

・幅がdx、

・縦の長さが(円を切り開いているので円周の公式より)2πx、

・高さがy＝f(x)

step 2:直方体を”x”で定積分する

上の立体をx(積分区間0→π/2)で定積分すると・・・

$$\int^{\frac{\pi}{2}}_{0}y\cdot 2\pi x dx$$

$y=\cos x$より、

今度は部分積分一回のみで済みます。xを微分する側・cosxを微分される側として

$$2\pi\int^{\frac{\pi}{2}}_{0}x\cos x dx$$

結果：$π^{2}-2π$・・・（答）

(基本パターンと比較/注意点)

当然答えは同じになります。

今回の問題よりもっと複雑な回転体(体積どうしの引き算や足し算が必要な場合など)では、バームクーヘン積分は更に有利になることがあります。

ただし、下のまとめにも書いているように、使用して良い場面/なんらかの説明を付けてから使うべき時、etc,,,が有るので見極めながらうまく使い分けましょう。

まとめと次回予告

・基本となる、置換積分を使う方法がメインなので、さまざまな問題を解いて確実に答えを出す様に復習しておきましょう。

・バームクーヘン分割については、あくまで(一)がダメor難しい場合や、検算に用いることと、

・↑は正式名称ではないので、記述式のテストなどでは答案の作り方に注意が必要です。