
格子点(数B数列)の超入門第一回
数列範囲の中でも、格子点に関する単元は漸化式、数学的帰納法とともに苦手な人が多い分野です。
格子点は『整数分野』や『数三の各分野』、「図形と方程式」等々、、にもオーバーラップして出題されることがあるので、この記事で基礎から標準レベルまで攻略していきましょう。
目次(タップした所へ飛びます)
格子点とは
格子点とは、次の『領域中の格子点』で図解しますが、xy座標平面上の各成分が整数である点のことをいいます。
基本的には、碁盤の目のように配置されている格子の数を求める問題がメインとなります。

<イメージ図1>
領域中の格子点
例えば下の<図2>の様にxy座標平面上の黄色で塗りつぶした格子点を求める様な問題です。
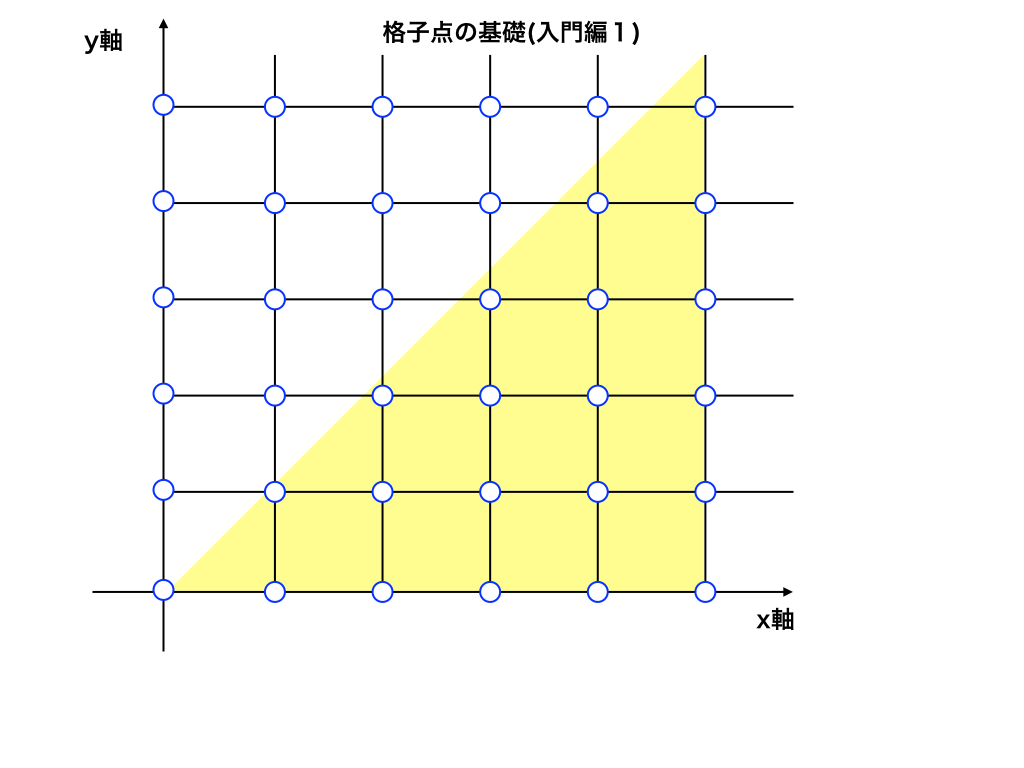
<イメージ図2>
線形計画法との関係
少し似た?イメージのものとして領域を利用して式の最大/最小値を求める線形計画法↓
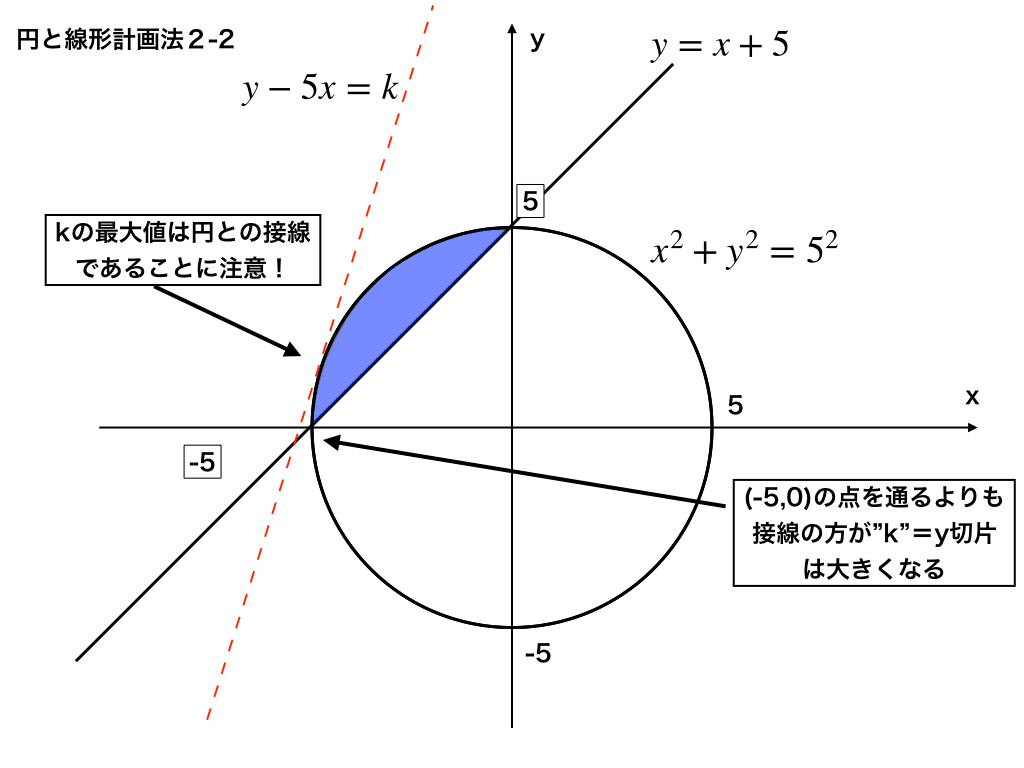
「線型計画法の記事はこちら」も時間が有ればチェックしてみましょう。
格子点の数え方
では、ここからはこの記事のメインとなる『格子点の個数を数える方法』について、一歩ずつ見ていきましょう。
1:タテで数える
y≦xとx軸、x=3で囲まれた領域に含まれる格子点《下図参照》の数を数えてみましょう。
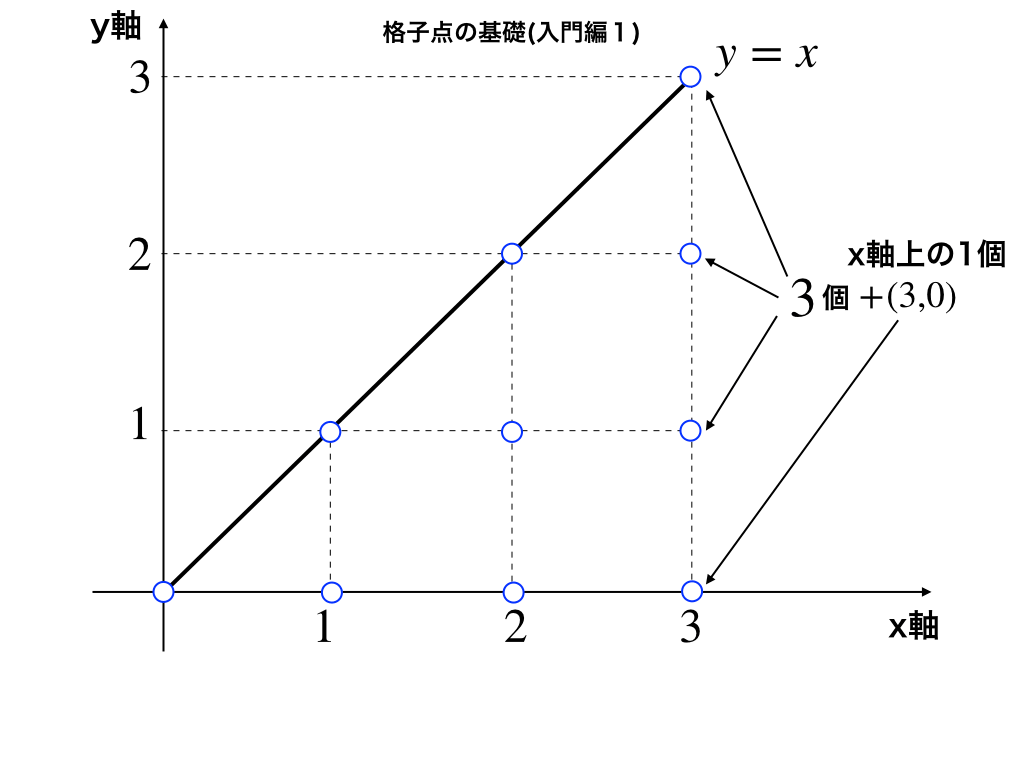
まず、y=xという直線上に一つずつ(0,0),(1,1)、(2,2)、(3,3)格子点があり、その下にある格子点の数は、0、1、2、3・・・と言うふうに等差数列になっています。
総和を考える(Σの利用を行う)と(参照:「数列の和とシグマ公式の解説記事」)
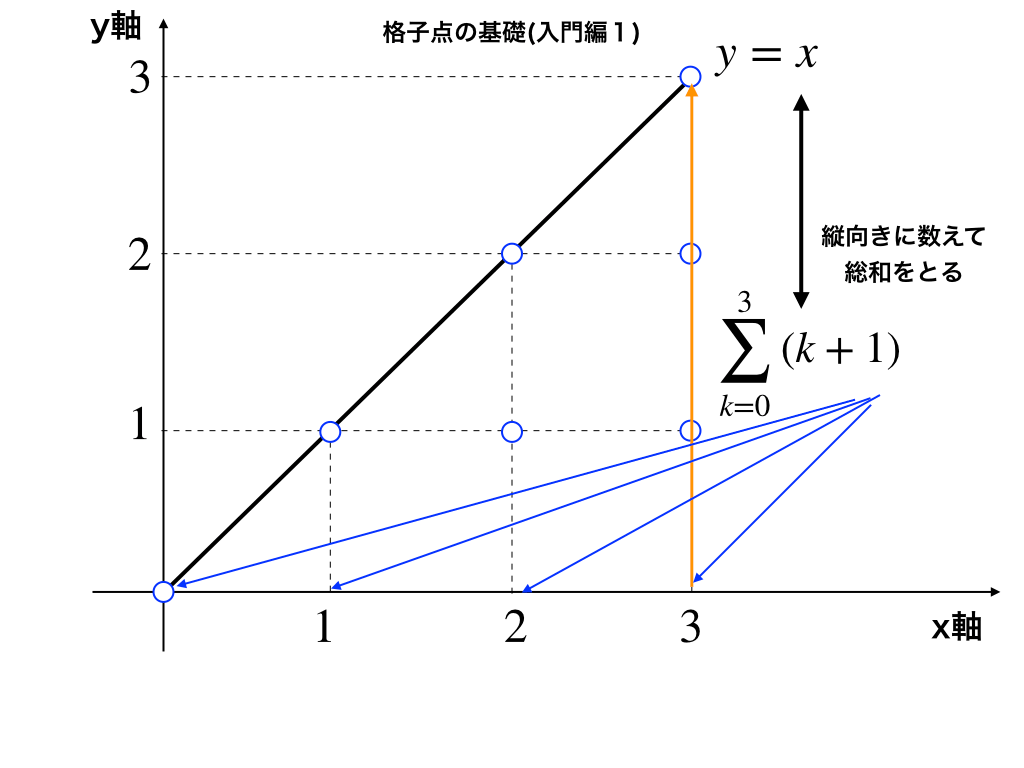
(x軸に垂直に数えていくと、図にあるようにxの値に対応した個数、プラスx軸上の点を加えます。)
したがって、この領域中の格子点を求めるにはシグマ公式を用いて簡単に計算できます。
$$\sum_{k=0}^{3}(k+1)$$
(ここではスタートがk=0となっているのでk=0のときとk=1〜のお馴染みのカタチに変型させておきます。)
$$1+\sum_{k=1}^{3}(k+1)$$
ヨコで数える場合
次は、縦方向では上手くいかない問題を見ていきます。
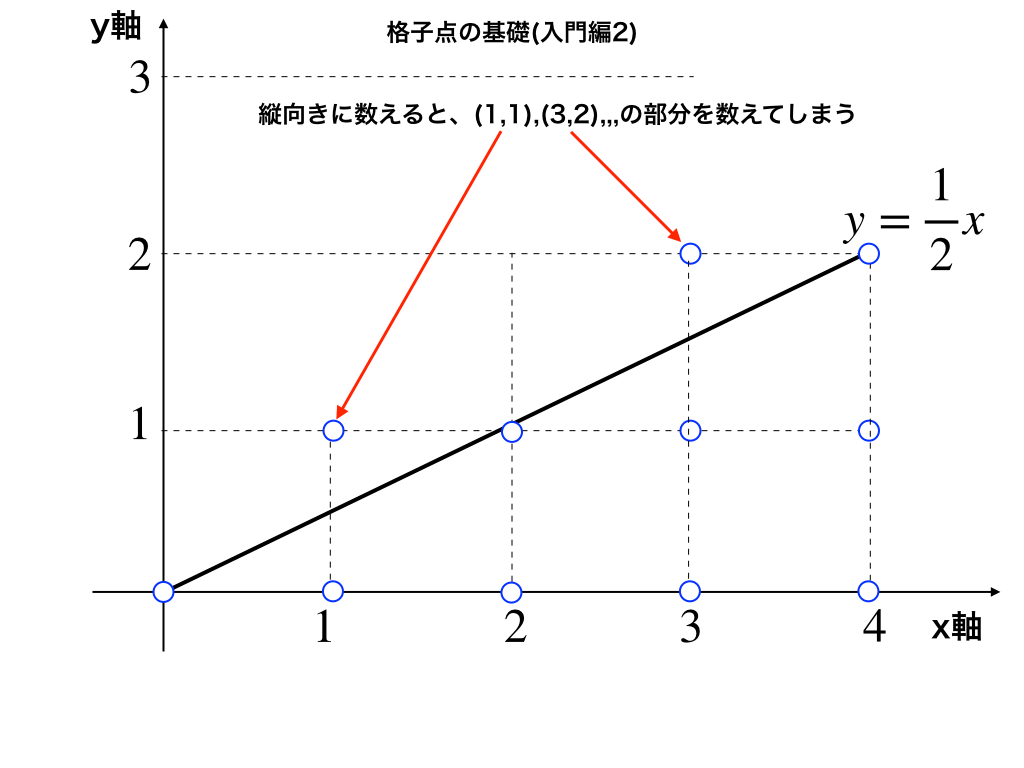
$$y=\frac{1}{2}x$$とx軸、x=4で囲まれた部分の格子点の数を求めてみます。
この様な場合に、縦向きに足し合わせる方法をとってしまうと、x=1、3、・・・とx=0、2、4・・・によって個数を区別して数えることが必要となってしまい面倒です。
(→偶奇で場合分けをすれば同様に計算できますが、これから紹介する方法ではその必要がないor最小限ですみます。)
そんな時は見方を少し変えて、横向きに足していく方法をとります。
格子点の個数まとめ
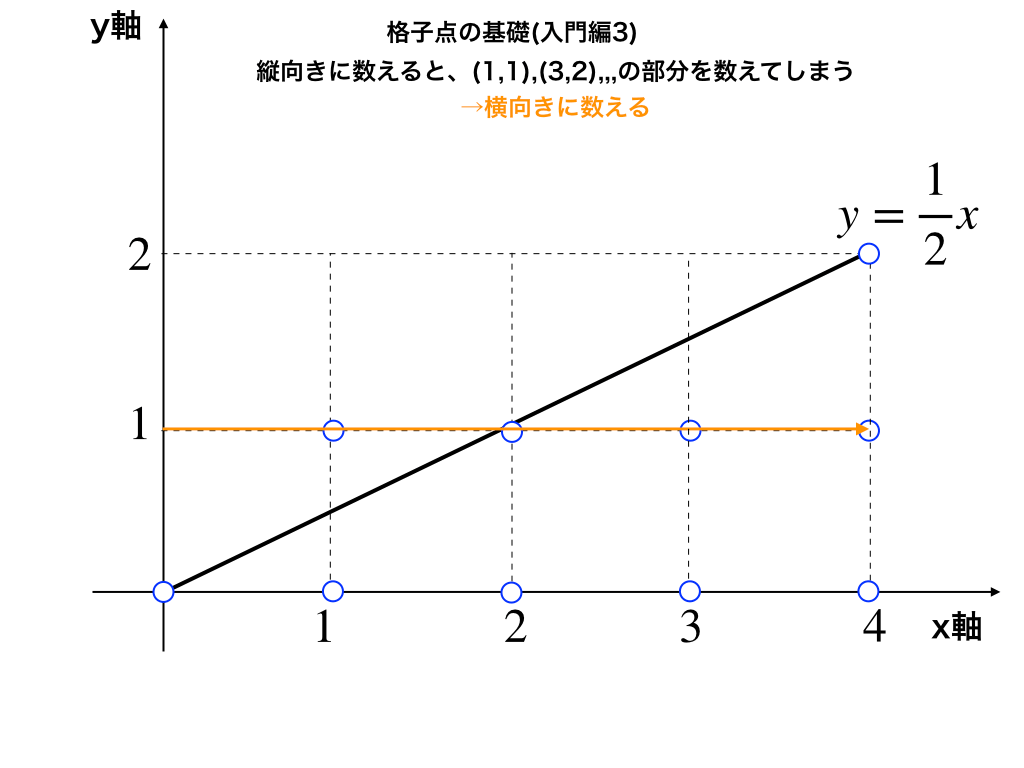
こう言った場合には、【x軸に並行=横向きに規則をつかんで総和を求める】ことによって楽になる場合があります。
y=0、1、2の時の格子点を数えると5個、3個、1個となって、確かに場合分けせずとも先ほどx=0、1、2、3、4で考えた時に発生した《余分な格子点》を計算せずに済むことが分かります。
(ここでは一般化する必要がないので、シグマを使わずに5+3+1=9(個)・・・(答)と出来ます。)
横向きに数える際にΣを使う問題は以下で扱います。
格子点の定着問題(現在追記中)
ここまでは【“対象とする領域”が単純なもの】でしたが、
・二次関数や
・円、
・直線など
が組み合わさった、複雑な領域に含まれる格子点を求める問題が徐々に出てきます。
その場合には、色々と工夫をする必要が出てくるので、具体的な応用問題を題材にして解説していきます。
格子点入門(1)まとめ
はじめに書いたように、格子点は整数・数列・確率・図形と方程式、etc,,,の様にあらゆる分野に現れ、最適化に関する学問や暗号理論等へと発展していきます。
入試でも難関大を中心に頻出するので、少しずつマスターしていきましょう!
数列や整数などの関連分野へ
最後までご覧いただきまして、ありがとうございました。
「スマナビング!」では、読者の皆様のご意見・ご感想を募集しています(全てに対応出来ない場合もございます)。
また、お役に立ちましたら、B!やシェアをしていただけると、とても励みになります。
・お問い合わせ/ご依頼/その他のご連絡は、ページ上部の【運営元ページ】よりお待ちしています。

