機械学習に必要な数学のロードマップと各単元を基礎から解説した記事まとめ

機械学習の理論を学んでみたい人向け!最小限の高校・大学教養レベルの数学

＜この記事の内容＞：機械学習の理論を学び始めたい人が、最低限知っておきたい数学の知識・分野を紹介し、そのそれぞれの詳細な解説記事へのリンクを総まとめしたページです。

＜この記事の対象者＞機械学習を初めて学ぶ人で、文系出身or理系でも卒後しばらく時間が経っていて０から学び直したい人。他にも、入門者向けの本でも難しく感じる人。

＜目標到達点＞高校1年生のレベルから、基本的な機械学習の解説本の数式が自力で理解できるレベルまで。(最終的に”機械学習エンジニア”や”データサイエンティスト(アナリスト/エンジニア) ＂を目指す！)

随時必要な分野の記事を追加していきますので、ブックマーク推奨です！

↓↓目次の中から読みたい記事をタップ！↓↓

機械学習の理解と数学の必要性・ロードマップ

このことはすでに色々な方が議論されていますが、近年では豊富に用意されたライブラリを用いることによって、数学の知識がそれほどなくとも”ある程度”のことはできるようになりつつあります。

逆に本格的なレベルに踏み込むならば、非常に高度な知識が必要とされるでしょう。

本記事はそのあいだに位置し、数式の羅列された本が読みづらい人を対象に、その都度調べながらでも読み進めることができる”数学の基礎体力”をつけることを目的にして作成しています。

機械学習・データサイエンスに必要な数字ロードマップ

以下のロードマップは、高校1年のレベルで学ぶ分野から”機械学習エンジニア”や”データサイエンティスト(アナリスト/エンジニア)”に必要な知識・スキルに至るまでの道のりをザックリまとめたものです。

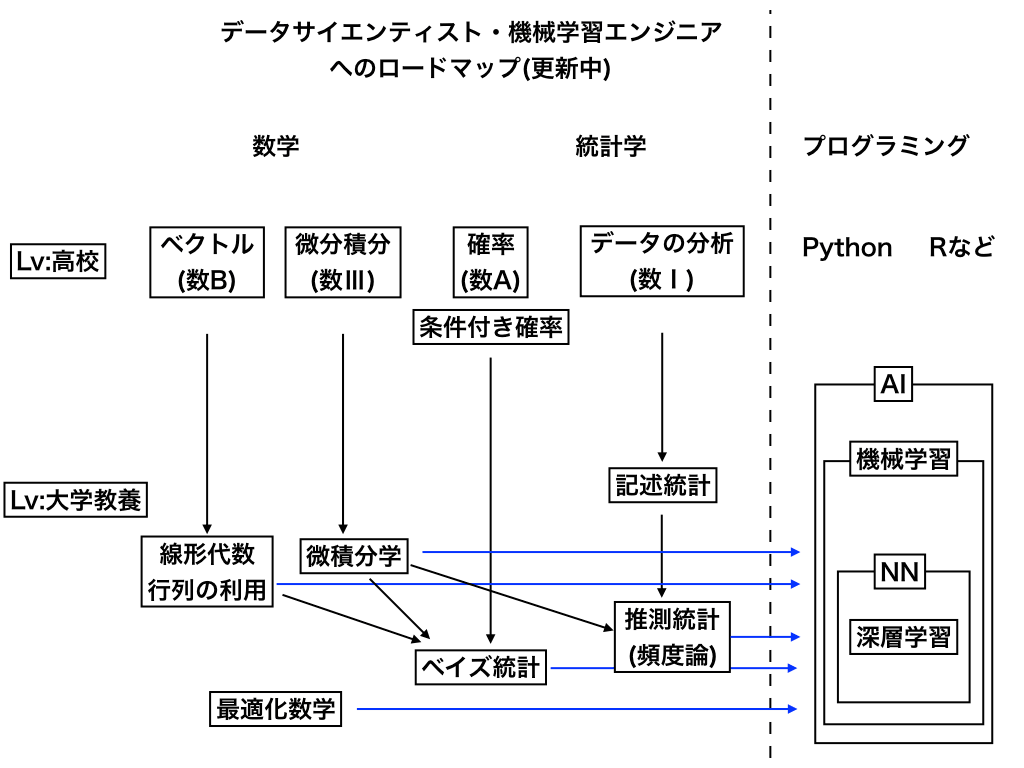
ここに書かれていない分野でも大切な物は多数あります。

が、(すべてを書き出しているときりがないので,,,)随時必要な時に紹介していきます。

ベクトル・行列などの線形代数編

まず、大量のデータを扱う際に必須の行列や、分類の基礎でも登場するベクトルなどを含む『線形代数』の分野からです。このページで扱う数学の中でも、まずはじめに『線形代数』を学ぶことをお勧めしています。

ベクトルの知識が０の人へ

完全に０からベクトルを学ぶ人は、以下のまとめ記事の冒頭部分を読んでみることをお勧めします。

「ベクトルとは？その基礎の紹介と応用記事まとめ」

内積・外積の意味と違い

ベクトルどうしのかけ算には、「内積」（・ドットで表すもの）と「外積」（×クロスで表すもの）があります。

それぞれ計算方法も、結果として出てくる数の種類（内積はスカラー：外積はベクトル）も違います。

さらに、”幾何的な”内積と”成分表示されたベクトル“の内積についても知っておく必要があるでしょう。

「ベクトルどうしのかけ算：内積」

「成分表示されたベクトルの内積」

「外積の計算法と意味」

法線ベクトルについて

“重みベクトル”などとして「法線ベクトル」はよく利用されます。

(法線とは、接線に対して垂直=なす角が90度であるものの事を言います。)

「法線ベクトルの意味と外積を使った求め方」

行列とは何か

以前(旧課程)では、高校数学C（ベクトルは高校数学B）で教えられていた『行列』について。

行列の各成分に数値を与えて並べる性質から、大量のデータを扱う機械学習・深層学習には行列は必須です。

また、行列は一般に非可換（かけ算の順序が変わると答えも変わる）など、これまでの普通の数とは違った面を持ちます。

「線形代数：超入門シリーズ:行列の意味から応用まで」

↑の記事では、行列の基礎から固有値問題、行列式、２次形式などの内容を網羅しています。

微積分・偏微分などの解析編

微分、特に偏微分は回帰分析の勾配降下法などでよく利用します。

その前に、高校数学２と３の範囲の微分・積分を確認しておきましょう。

微分の定義

そもそも、微分とは一体なんなのか高校レベルでの解説です。

必要に応じて、極限の記事も参照してみてください。

「微分とは、導関数と微分係数の違い」

高校数学での微分法

「微分/積分とその応用記事（数学３＋α）」

合成関数の微分も次の項の偏微分と合わせて知っておくと良いです。

「合成関数の微分と対数微分法」

多変数関数の微分・偏微分

偏微分は、これまでの微分と違い(2変数関数などの)変数がいくつもある関数を微分する時に必要です。

言葉だけでは非常に難しそうですが、以下の記事を読んでみると、そこまで大変ではないと感じることができるはずです。

「偏微分とは？やり方と意味を紹介」

ラグランジュの未定乗数法(偏微分応用)

最適化を行うにあたって、機械学習の様々なアルゴリズム（SVM,KKT,etc,,,)で最大・最小値をを求める場面が出てきます。

ラグランジュの未定乗数法の解説

上の記事では、その手法の一つである未定乗数法について詳しく紹介しています。

深層学習の活性化関数：シグモイド関数(曲線)を学ぶ

ニューラルネットワーク、深層学習において、活性化関数として頻繁に用いられる『シグモイド関数(曲線)』の性質と、ロジスティック方程式という微分方程式の関係などを「シグモイド関数とロジスティック方程式(コラム)」の記事で紹介しています。

統計学と必要となる数学編

中学・高校では「場合の数と確率」や「データの分析」という単元で学びます。

『分類』などで条件付き確率を使ったり、パラメーターの検証に統計学の知識が必要になることが多く、そのための前準備となる単元です。

場合の数と確率全般~ベイズの定理について

ほぼ全ての「場合の数・確率」の記事は以下にまとめています。

その中から、特に機械学習に重要なものはここでもまとめておきます。

「場合の数と確率の解説記事まとめ」

完全に０から学ぶ場合は、順列組み合わせとは？といったレベルから始める必要があります。

「順列と組み合わせの違い」

特に確率・統計において『条件付き確率』の考え方は非常に大切です。

「条件付き確率がわかる！不良品や検査の確率まで」

条件付き確率は、『ベイズの定理』の理解に必須であり、ひいてはベイズ統計学を用いたベイジアンフィルター・ベイジアンネットワークにつながっていきます。

データの分析→記述統計学へ

＜数１：データの分析と数B：確率分布と、統計的な推測についての記事を追加予定です＞

データの分析

第1回：「中央値・平均値・最頻値と四分位数の求め方と箱ひげ図の書き方」

第2回：「データのばらつきを表す『分散・標準偏差』の求め方」

第3回：「共分散と相関係数の求め方と意味」

第4回：「変数変換とデータの標準化の仕方」

統計学入門シリーズ

本格的な推測(推計統計学)を基礎から解説していくシリーズです。

第一回：「統計学とは？記述・推計統計とその導入」

確率分布・推測統計と検定

第一回で基本的な統計学の学び方を紹介しました。

第二回からは統計学においてあらゆる局面で必要になる『様々な確率分布』などを紹介していきます。

「統計学(2)：離散/連続型確率分布を分かりやすく」

「統計学(3)：同時確率分布とE[X]、V[X]などの演算子・公式」；期待値や分散について、解説しています。

「ベルヌーイ分布と二項分布」

(現在重要な確率分布に付いて更新中です)

「統計学とデータの分析の記事一覧」

対数関数・三角関数や数列の記号など（その他）

この項では、微分や統計などと関連して頻繁に利用する記号や、関数などの計算方法やルーツについての確認を行います。

具体的には、尤度関数で用いる『対数関数』・cos類似度で使用する『三角関数の基礎』などの範囲を復習していきます。

Σ記号について

数列の和・総和を意味するシグマ（Σ）についての解説です。

「シグマ記号の計算のルールと数列の和の公式」

対数関数の記事

対数は、「真数」の掛け算を対数の足し算に変換できる特徴から、尤度関数などで必要となります。

「指数・対数とは？その意味から計算法則まで」

また、自然対数の底”e”については、「ネイピア数"e"の意味と歴史(コラム)」で詳しく紹介しています。

三角関数（cos類似度）などの基本

ベクトルの内積などと関連して、三角関数も非常に重要な関数です。

「三角関数の公式や基礎などのまとめ」

領域と線形計画法

高校２年生の数学（図形と方程式）の知識を使って、「不等式の条件を満たす式の最大・最小（線形計画法）」←で『線形計画法』の基礎を解説しています。

機械学習・データサイエンスの数学シリーズ一覧

ここで紹介してきたのは、初めに書いた通りごく初歩的なレベルです。

これらをもとにして、さらに高度な数学についてはそれぞれの専門書などで学んでいってください。

高校数学で学び始める、機械学習

第0回:「いまここです」

第1回:「単回帰分析とは何か？機械学習１」

第2回:「最急降下法（勾配降下法）のための偏微分」

第3回:「パラメータの更新式と勾配降下法のイメージ：機械学習３」

第4回：「重回帰分析とは？（作成中）」

最後までご覧いただき、ありがとうございました。

「スマナビング！」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。

ご質問・ご意見がございましたら、ぜひコメント欄までお寄せください。

また、B！やシェア、Twitterのフォローをしていただけると励みになります。

・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。