共分散と相関係数の求め方と意味/散布図との関係を分かりやすく解説

データの分析(3)・統計学

共分散と相関係数

＜今回の内容＞「データ（２）分散と標準偏差の求め方」に引き続き、二つのデータの関係を分析するための「共分散・相関係数」の求め方を前回までの内容を復習しながら解説します。

＜この記事で習得できる事＞

・「２変量データから、相関係数が求められるようになる」、

・「散布図と相関係数の関係が理解できる」。

共分散の計算方法と散布図

前回、前々回と「身長」という一つのデータ（これを１変量データと言います）の代表値や四分位数・箱ひげ図、さらにデータのばらつきを表す分散・標準偏差の求め方まで紹介してきました。

２変量データの共分散

次に取り組むのは、「２変量」（例えば『身長』と『体重』）の間にどのような関係があるかを数値化して調べる方法です。

この記事では以下の１０人分の身長・体重のデータを使用することにします。

＜10人分のデータ＞

ここからは計算の都合上、１人目の身長をa₁(cm),体重をb₁(Kg)・・・n人目の身長をa_n(cm),体重をb_n(Kg)とおきます。

散布図上にデータをプロットする

実際に上でまとめたデータを『散布図』というグラフにしてみます。

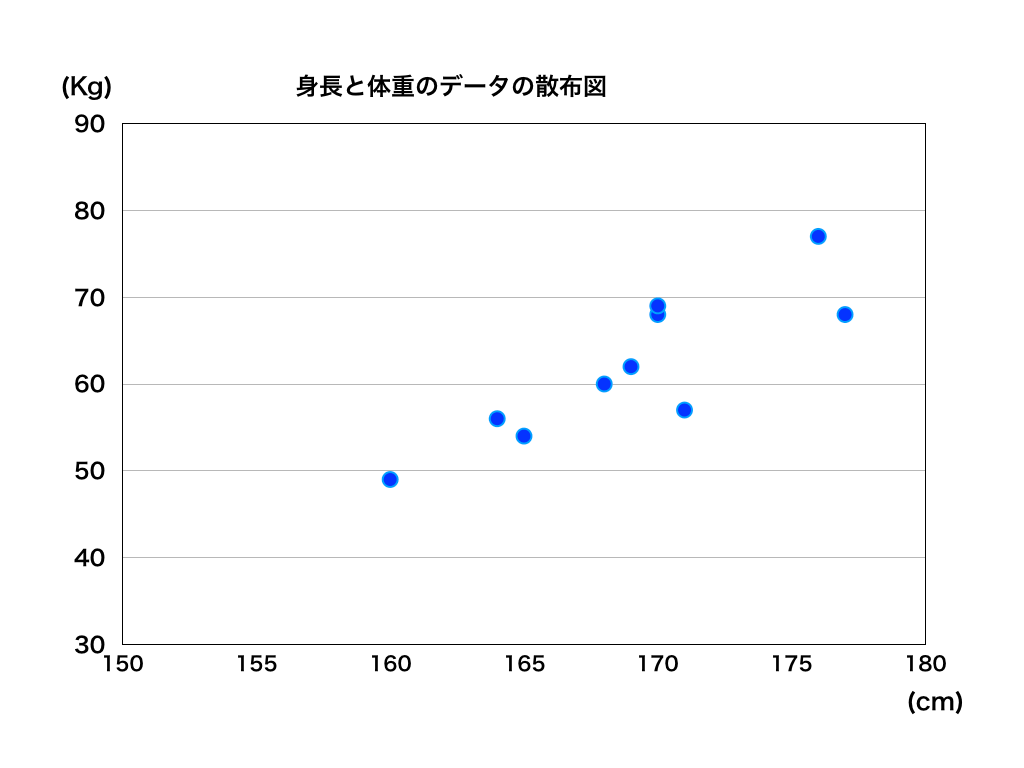
この図を見ると、身長が高いほど体重も増えている様子がわかります。この関係を客観的な数値で表そうという考えが次の項で紹介する【相関係数】です。

共分散の求め方

以下の図のとおり、相関係数を求めるためには先に”共分散”を求める必要があります。

１変量のデータの時

$$分散=\frac {(1番の値-平均)^{2}+…(n番の値-平均)^{2}}{n(データの個数)}$$の式で求めました。

共分散では、全員の身長の平均を\(\bar {a}\)、同じく体重の平均を\(\bar {b}\)として、

$$共分散=\frac{(a_{1}-\bar {a})(b_{1}-\bar {b})+…+(a_{n}-\bar {a})(b_{n}-\bar{b})}{n)}$$

発展：シグマ記号を用いて（「シグマ記号の意味と計算法則の記事」）もう少し簡潔に書くと、$$\frac {\sum ^{n}_{k=1}( a_{k}-\bar {a})( b_{k}-\bar {b}) }{n}$$

という式で表すことができます。

文字だけでは分かりづらいかと思うので、先ほど挙げた１０人のデータをもとに共分散を計算してみましょう。

実際に計算してみる

まず、１０人の身長の平均は169(cm),体重の平均が62(Kg)なので、

１人目の（身長ー平均)(体重ー平均)＝6

2人目の（身長ー平均)(体重ー平均)=117

・・・

10人目の（身長ー平均)(体重ー平均)＝０

となり、共分散の式の(分子)＝337と求まります。これを(分母の)10で割ることで、共分散＝33.7//と計算できます。

身長・体重それぞれの標準偏差も求めておく

次の項で扱う相関係数では、二つのデータの標準偏差が必要なので、前回「偏差平方と分散・標準偏差の求め方」で学んだ通りに、それぞれの標準偏差をあらかじめ求めておきます。

通常の式は前回の記事で紹介しているので、ここでは先ほどの共分散の時と同様にシグマ記号を使った、簡潔な表記をしておきます。

$$身長の標準偏差＝\sqrt {\frac {\sum ^{n}_{k=1}( a_{k}-\bar {a}) ^{2}}{n}}$$

$$体重の標準偏差=\sqrt {\frac {\sum ^{n}_{k=1}( b_{k}-\bar {b}) ^{2}}{n}}$$

それぞれをk=1(つまり一人目)からn人目(今回n=10なので)10人目までのそれぞれの標準偏差は、

$$身長：\sqrt {24.2}$$

$$体重：\sqrt {64.4}$$

相関係数の計算と範囲・散布図との関係

では、共分散が求まったところで、相関係数を求めましょう。

先ほど書いたように、相関係数は『共分散』と『二つのデータの標準偏差』を用いて次の式で計算できます。：$$\frac{データ1,2の共分散}{(データ1の標準偏差)(データ2の標準偏差)}$$

ここでの『データ１』は身長・『データ２』は体重です。

相関係数の値の範囲

相関係数は-1から１までの値をとり、値が０のとき全く相関関係がなく１に近づくほど正の相関（右肩上がりの散布図）、-1に近付くほど負の相関（右肩下がりの散布図）になります。

相関係数を実際に計算する

相関係数の値を得るには、前回までに学んだ標準偏差と前の項で学んだ共分散が求まっていれば単なる分数の計算にすぎません。

今回では、$$\frac{33.7}{(\sqrt {24.2})(\sqrt {64.4})}≒\frac{337}{395}≒0.853$$

よって、相関係数はおよそ”0.853”とかなり１に近い＝強い正の相関関係があることがわかります。

相関係数と散布図

ここまでで求めた相関係数（”0.853”）と散布図の関係を見てみましょう。

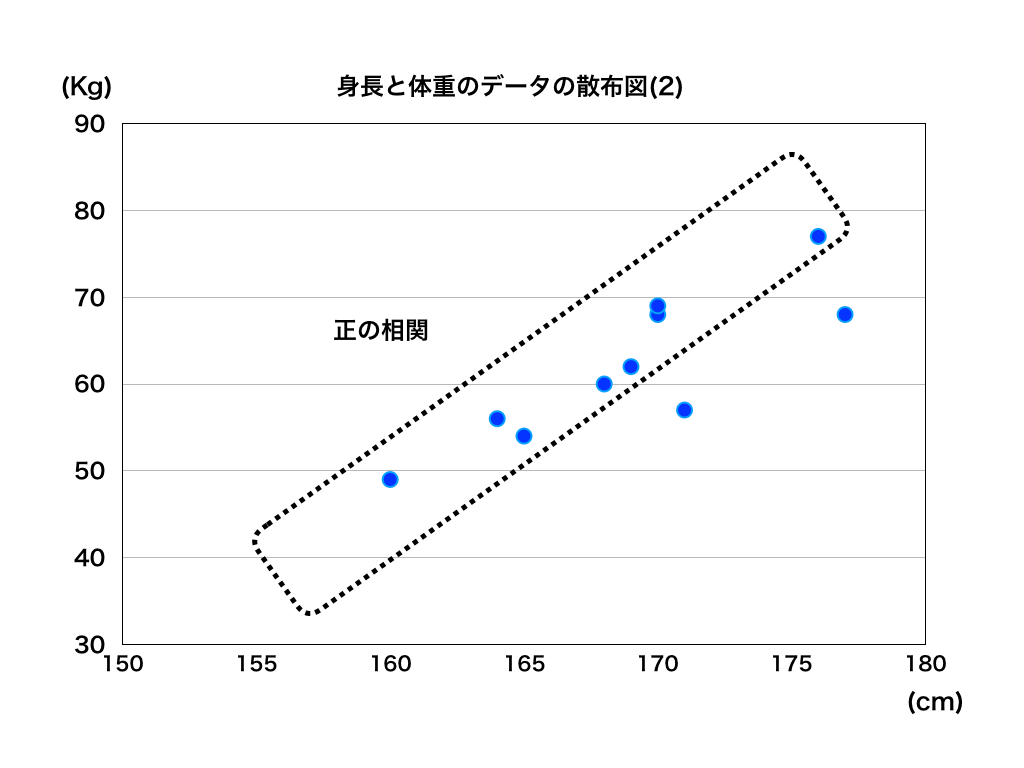
相関係数はおよそ0.853だったので、最初の散布図を見て感じた”身長が高いほど体重も多い”という傾向を数値で表すことができました。

まとめと次回「統計学入門・確率分布へ」

・共分散と相関係数を求める単元に関して大変なことは”計算”です。できるだけ素早く、ミスなく二つのデータから相関係数まで計算できるかが重要です。

そして、大学入試までのレベルではそこまで問われることは少ないですが、『相関関係と因果関係を混同してはいけない』という点はこれから統計を学んでいく上では非常に大切です。

次回からは、本格的な統計の基礎の範囲に入っていきます。

データの分析・確率統計シリーズ一覧

第1回:「代表値と四分位数・箱ひげ図の書き方」

第2回:「偏差平方・分散・標準偏差の意味と求め方」

第3回:「今ここです」

統計学第1回:「統計学の入門・導入：学習内容と順序」

今回もご覧いただき有難うございました。

「スマナビング！」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。

ご質問・ご意見がございましたら、是非コメント欄にお寄せください。

いいね！や、B！やシェアをしていただけると励みになります。

・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。