内積:ベクトルどうしの掛け算を分かりやすく解説
<この記事の内容>:ベクトルの掛け算(内積)について0から解説し、後半では実戦的な内積を扱う問題の解き方やコツを紹介しています。
『内積』は、高校数学で習うベクトルの中でも、特に重要なものなのでぜひじっくり読んでみて下さい。
関連記事:「成分表示での内積(第二回:空間ベクトル)」
目次(タップした所へ飛びます)
内積とは何か?ベクトルの掛け算の意味
そもそも『内積』とは何なのか?はじめから見てみましょう。
内積と外積:ベクトルの掛け算は2種類ある!
前回、ベクトルの足し算と引き算を紹介しました。→「ベクトルが分からない?はじめから解説します」
そうすると、掛け算もあるのではないかと思うのは自然な事だと思います。
実はベクトルの足し算、引き算と違ってベクトルには2種類の全く違う「掛け算」が存在します!
一つは内積とよばれるもので、『ベクトル』と『ベクトル』の間に、掛け算であることを示すための『ドット(・)』を書きます。(このことから内積のことをドット積と呼ぶことがあります)高校で習うのはこちらの掛け算です。
内積(ドット積)の定義
では早速、その内積(ドット積)の定義とそのイメージ図を紹介していきます。
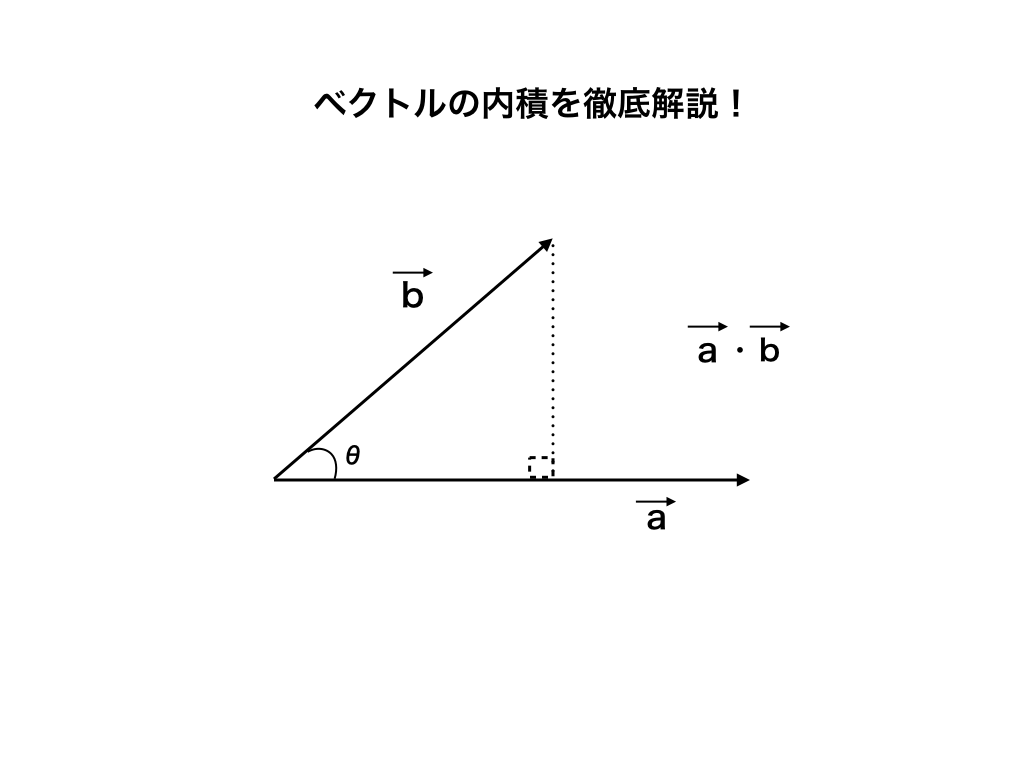
ベクトルと言うのは「向き」と「大きさ」の二つの情報を持っていましたが、ベクトルの内積では以下の式の通り、「大きさ」・cosθ(−1≦cosθ≦1)つまりスカラー量しか計算しません。
したがって、ベクトル量どうしの掛け算にも関わらず、答えは「数=スカラー量」だけが出てきます。
内積の定義の式:ベクトルA≠0、ベクトルB≠0のもとで、
$$\overrightarrow {a}\cdot \overrightarrow {b}=| \overrightarrow {a}| | \overrightarrow {b}| \cos \theta $$
この式を日本語にすると、
『ベクトルAとベクトルBの内積は、”ベクトルAの大きさ”掛ける”ベクトルBの大きさ”掛ける”cosθ”』
(但し、ベクトルAとベクトルBのなす角をθとして、0°≦θ≦180°)
なす角というのは、ベクトルAとベクトルBの始点をそろえた時の間の角度のことです。
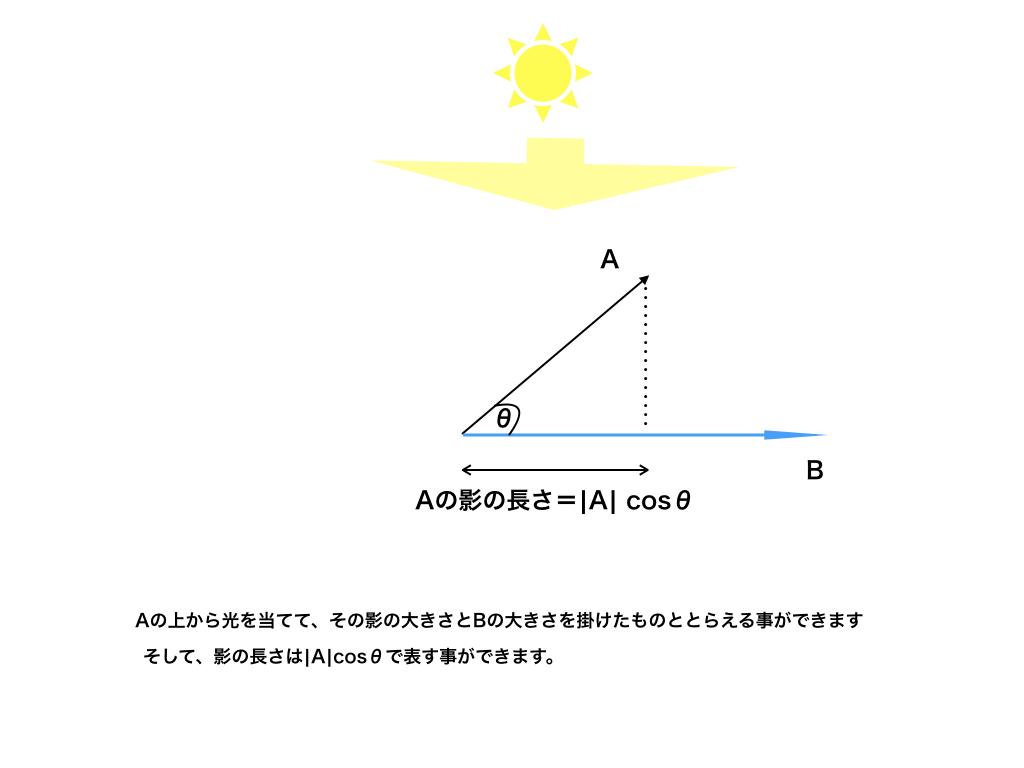
<図1:内積の図形的な意味(イメージ)>
これが一つ目の掛け算(内積)の定義です。
もうひとつの掛け算「外積」
2つ目は外積といって、記号は普通の掛け算と同じ(×:クロス積とも言います)を使います。
外積については、高校範囲外ですが、興味のある人は
→「外積とは?ベクトルのもう一つの掛け算:内積との違いや計算法を解説」を
(内積を理解した後で)読んでみて下さい。
(外積の場合はベクトル量同士を掛けて、出てくる答えもベクトル量になります)
同一ベクトル同士の内積
いま、ベクトルA≠0があるとします。このベクトルAどうしの内積はどうなるでしょうか?
(先ほどの図1を参考にしながら読み進めて下さい)
定義に従って計算すると、同じベクトル=重なっているので、なす角θ=0°だから、
A・A=| A|| A|cos0°
\(\vec {a}\cdot \vec {a}=|\vec {a}||\vec {a}| \cos 0^{\circ }\)
cos0°=1より
\(\vec {a}\cdot \vec {a}=| \vec {a}| ^{2}\)
したがって、ベクトルAの絶対値の2乗 になります。
ベクトルの大きさ(=長さ)とベクトルの二乗
すなわち、同じベクトル同士の内積は、そのベクトルの「大きさ(=長さ)」の二乗になります。
これも大変重要なルールなので、しっかり覚えておいて下さい。
内積の計算のルール
(普通の文字と同様に計算出来ますが、 A・ Aの時、 Aの二乗ではなく、上述したように絶対値Aの二乗になることに注意して下さい!)
交換法則
交換法則とは、以下の様にベクトル同士を掛ける順番を逆(交換)にしても同じ値になる、という法則です。
当たり前の様に感じるかもしれませんが、大学で習う「行列」では、掛ける順番で結果が変わる事がほとんどなのです。
<参考:「行列同士の掛け算を分かりやすく!」>
\(\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}\)
分配法則
分配法則は式で見た方が早いかもしれません。
\(\vec{p}\cdot (\vec{q}+\vec{r})=\vec{p}\cdot \vec{q}+\vec{p}\cdot \vec{r}\)
ではここまでのルールと計算を使った例を見ていきましょう。
例1)
\(( \overrightarrow {a}+\overrightarrow {b}) ( \overrightarrow {a}) =\overrightarrow {a}\cdot \overrightarrow {a}+\overrightarrow {a}\cdot \overrightarrow {b}\)
\(=| \overrightarrow {a}| ^{2}+\overrightarrow {a}\cdot \overrightarrow {b}\)
( A +B)( A)
= A・ A+ A・B
=|A| ^2 + A・B
例2)
\(( \vec {a}+\vec {b})( \vec {a}+\vec {c}) =\)
\(| \vec {a}| ^{2}+\vec {a}\cdot \vec {b}+\vec {a}\cdot \vec {c}+\vec {b}\cdot \vec {c}\)
( A +B)( A +C)
= |A| ^2 + AC + AB +BC
ベクトルの内積を使う問題の解法とコツ
ここからは、上で学習した内積の定義、性質と計算のルールを用いて、実際に問題を解きながら回答の流れやコツ、pointなどを紹介します。
絶対値付きのベクトルの式が出て来る問題
これは解き方が決まっているので、例題を通して身に付けて下さい。
point!絶対値の中にベクトルの式があれば、二乗せよ!
(例題1)
\(| \vec {a}| =3,| \vec {b}| =4,| \vec {a}+\vec {b}| =7\)のとき、ベクトルaとベクトルbの内積を求めよ。
point!に従って、絶対値の式を2乗してみましょう。
$$| \vec {a}+\vec {b}| ^{2}=| \vec {a}| ^{2}+2\vec {a}\cdot \vec {b}+| \vec {b}| ^{2}$$
\(\begin{aligned}49=9+2\vec {a}\cdot \vec {b}+16\\
⇔ 24=2\vec {a}\cdot \vec {b}\\
⇔ \vec {a}\cdot \vec{b}=12\end{aligned}\)
よって、ベクトルa,bの内積は12・・・(答)
(例題2)内積の定義を思い出そう!
(例題2):|A|=2 |B|=3 A・B= 3の時 ベクトルAとベクトルBのなす角θを求めよ。
\(| \overrightarrow {a}| =2,| \overrightarrow {b}| =3,\overrightarrow {a}\cdot \overrightarrow {b}=3,θ =?\)
ベクトルの内積の定義は$$\overrightarrow {a}・ \overrightarrow {b}=| \overrightarrow {a}| | \overrightarrow {b}| \cos θより$$
変形すると\(\cos\theta=\frac {\vec {a}\cdot \vec {b}}{| \overrightarrow {a}|| \overrightarrow {b}| }\)となるので
$$\cos \theta =\frac {3}{2\cdot 3}=\frac {1}{2}$$
\(\begin{aligned}0^{\circ }\leq θ \leq 180^{\circ},\cos θ =\frac {1}{2},\\
\theta=60^{\circ}\end{aligned}\)
よって、ベクトルaとbのなす角θ=60°・・・(答)
内積と垂直条件
ベクトルの内積の考え方を応用すると、ベクトル同士が垂直である為の条件を導くことができます。
こちらも先ほどの図を参考にして下さい。
始点が揃った2つのベクトル A、ベクトルBが垂直の時:
なす角θ=90°になるので内積の定義より『cos90°=0』
$$\overrightarrow {a}\cdot \vec {b}=|\vec {a}||\vec {b}| cos90^{\circ }=0$$
A・B=|A||B| cos90°=0
したがって、垂直条件は内積= 0になります。
ベクトルAとBが垂直な時は、上から光を当てた”影の長さは0になる”事が<図1>からイメージできるかと思います。
0に何を掛けても0なので、計算式だけでなく図でも"垂直条件=内積が0"という事が分かる様にしておきましょう!
内積のまとめ問題
ここまで学んできたベクトルの内積の知識や解法を使って、次のまとめ問題を解いてみましょう。
(まとめ):ベクトルAとベクトルBが、|A|=3、|B|=2、 A・B=6を満たしている時、 |6 AーB|の値を求めよ。
\(| \overrightarrow {a}| =3,| \overrightarrow {b}| =2,\overrightarrow {a}\cdot \overrightarrow {b}=6\)
\(| 6\vec {a}-\vec {b}| =?\)
point!:絶対値があれば、2乗せよ!の方針に従って、まず求めたい|6A-B|を二乗してみます。
\(\begin{aligned}| 6\overrightarrow {a}-\overrightarrow {b}| ^{2}=36| \overrightarrow {a}| ^{2}-12\vec {a}\cdot \vec {b}+| \vec {b}| ^{2}\\
⇔ 36× 9-12× 6+4=256\end{aligned}\)
二乗して展開することで、『ベクトルAの二乗;ベクトルAとBの内積;ベクトルBの二乗』をそれぞれ代入すれば問われている”|6A-B|”の2乗が求まります。
\(| 6\vec {a}-\vec {b}| ^{2}=256>0より\)
あとは、今求めた値が2乗した数なのでルートを取り
(この時、±16となりますが、|6A-B|は0以上なので、+の方の値が答えとなります。)
\(| 6\vec {a}-\vec {b}| =16\)
従って、 |6 AーB|の値は16//
内積のまとめとベクトルの関連記事(成分表示での内積へ)
ベクトルの内積は平面・空間ベクトルを問わず必ず使う物なので、基本的な計算と定義、今日のpoint!は必ず抑えておいて欲しいです。
また、ベクトルは物理と深く関わる非常に面白い分野なので、そのことについても紹介して行きたいと思います。→<参考:「物理基礎(力学)のためのベクトルと三角比」>
お役に立ちましたら、次のまとめ記事を読んで、更にベクトルを得意分野にしましょう!
成分表示での内積・垂直/平行条件
この記事では、『成分表示を使わない「内積」』を解説してきました。
次の記事で成分表示での内積と、それを利用した「垂直条件」・「平行条件」を例題とともに解説していきます。>>「ベクトルの成分表示での(内積)計算とその応用」<<を読む。
ベクトルの総まとめ記事
以下の総まとめページは、ベクトルについて解説した記事をやさしい順に並べて、応用問題まで解ける様に作成したものです。「ベクトルとは?ゼロから始める徹底解説記事12選まとめ」をよむ。
「スマナビング!」では、読者の方からのご意見・記事リクエストを募集しております。
ぜひコメント欄までお寄せください。

