
第4回:法線ベクトルの応用
この記事は、「【空間ベクトル】平面の方程式の求め方(1)【数B】」の続編として、
空間中で直線や平面に垂直な『法線ベクトル』について解説していきます。
・法線ベクトルの具体的な使い方が分からない方や、
・空間図形をベクトルで解く方法を詳しく知りたい方は必見です。
・記事の最後には、実際に京都大学で出題された「空間に存在する平面に対称な点」を求める問題を掲載しました。
・最難関大の入試問題でも、キッチリとこの記事を読めば、対処出来ることが分かってもらえるかと思います。
目次(タップした所へ飛びます)
法線ベクトルの意味と求め方
具体的な問題に入る前に、『法線ベクトル』について復習しておきます。
(第一回を読んでいない方はぜひ先にお読みください→「【空間ベクトル】平面の方程式の求め方【数B】」)
法線ベクトルとは
・直線、または平面に垂直なベクトルのこと
法線ベクトルの求め方の復習
こちらも簡単に、法線ベクトルの求め方を振り返っておきます。
外積の利用
パラメータ消去
平面の方程式の利用
外積の利用(三点が与えられている場合)
同じ平面を通る三点(O,A,B,が与えられている時、OA×OB:の外積が法線ベクトルになります。
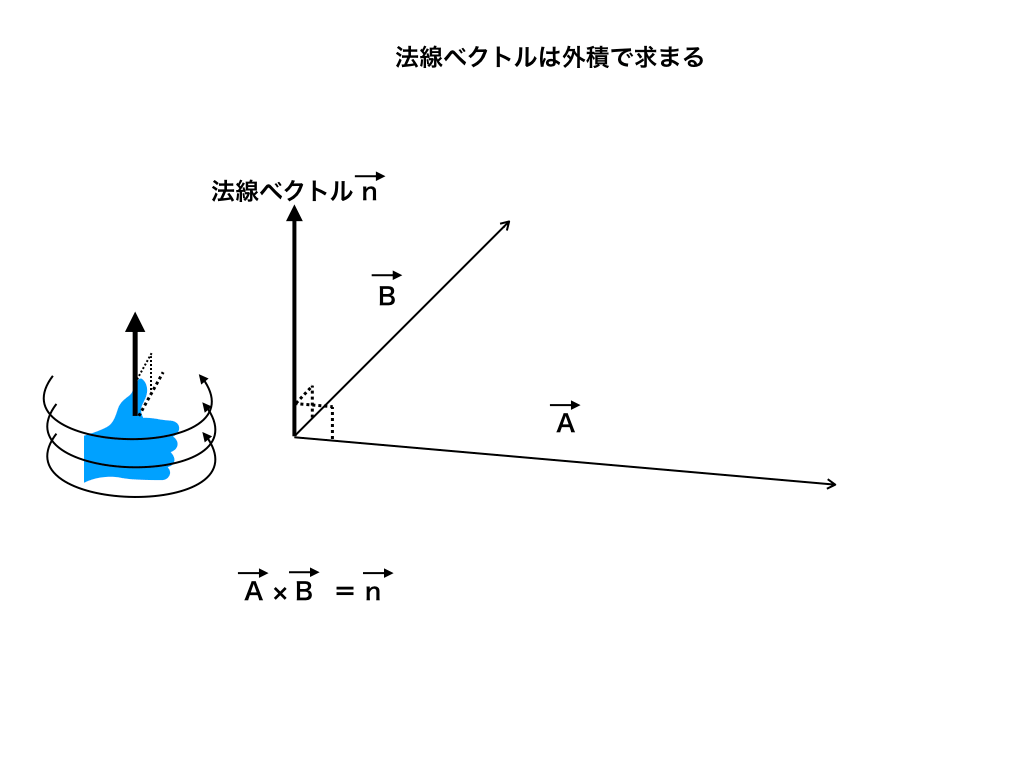
\(\overrightarrow {OA} ×\overrightarrow{OB}= \vec {n}\)
もう一つ忘れてはならない方法は、「パラメータ消去」によって求めることです。
この方法は、平面上にOAB以外の点Pをおいて成分表示し、その途中で出てくるパラメーター2つを連立方程式で解く、というものです。
一般的ではありますが、外積を利用した場合に比べて、計算がかなり煩雑になるというデメリットがあります。
(詳しいパラメーター消去の方法は→「平面の方程式の記事」で解説しているので、ぜひそちらもご覧ください。)
3つ目の手段は次の項で解説します。
平面の方程式が与えられている場合
平面の方程式:ax+by+cz+d=0 が与えられている場合、法線ベクトル\( \vec {n}は、 \vec{n}=(a,b,c)\)
上の様に、方程式のx、y、zの係数が法線ベクトルの各成分になります。
空間ベクトルの問題への応用(なす角→内積と法線ベクトル)
では、実際に法線ベクトルを使って、空間図形の問題を解く方法を紹介していきます。
まずは、2直線・2平面のなす角を求める問題です。
内積の公式(復習)
ベクトルの内積については→「ベクトルの内積とは?ベクトルどうしのかけ算の正体」で詳しく解説しています。
\(\vec {a} \cdot \vec {b}=|\vec {a}||\vec {b}|cosθ\)
内積(成分表示)
ベクトルの成分表示での「内積」については→「ベクトルの成分表示と内積」の記事をご覧ください。
$$\vec{a}=(a_{x},a_{y}),\vec{b}=(b_{x},b_{y})$$のとき、$$\vec {a} \cdot \vec {b}=a_{x}b_{x}+a_{y}b_{y}$$
準備:直線同士のなす角
2直線(ℓとmとします)のなす角は、\(ℓの法線ベクトル\vec {n_{ℓ}}\) と\(mの法線ベクトル \vec {n_{m}}\)のなす角と同じになります。
(※注意!“直線”同士のなす角は0°≦θ≦90°、“ベクトル”同士のなす角は0≦θ≦180°と範囲が違うことを頭に入れておいてください!)
例題(直線のなす角)
(例題1)いま以下の方程式で表される、2つの直線ℓとmがある。このℓとmがなす角θを求めよ。
ℓ:2x+y+2=0
m:x+3y+5=0
直線ℓ、mの法線ベクトルは、それぞれ
\(n_{ℓ}=(2,1),n_{m}=(1,3)\)で表すことができ(『法線ベクトルの求め方』の3番目)
\(n_{ℓ}とn_{m}\)の内積より、$$cosθ=\frac {2\cdot 1+1\cdot 3}{\sqrt {2^{2}+1^{2}} \sqrt {1^{2}+3^{2}}}$$
よって、$$cosθ=\frac {1}{\sqrt {2}}$$
cosが√2分の1になるのは、0≦θ≦180°の範囲ではθ=45°のみなので、法線のなす角は45°。
2直線ℓとmのなす角も同じ値なので、
45°・・・(答)
平面同士のなす角を求める問題
次に、2“直線”から少し発展した2つの平面の問題を考えます。
具体的には、2つの平面のなす角を法線ベクトルを使って求めてみます。

<平面どうしがなす角を求める>
上の図のように、平面と平面が交差している時、その間の角度を平面どうしが成す角といいます。
そしてこの角度は、直線どうしの時と同様に、2平面(平面πと平面ρとします)それぞれの“法線ベクトルのなす角”と同じになります。
(先述したように”なす角の範囲が面(直線)とベクトルで異なる”ので、法線ベクトルのなす角θが90°以上の時には、180°ーθが平面どうしのなす角となります。)
例題(2平面のなす角)
方程式が『-x+2y+z=4』で表される“平面π”と、が『-2x+y-z=4』で表される“平面ρ”がなす角を求めよ。
<解法の手順>
(一)それぞれの平面の方程式から法線ベクトルを求める。
平面πの法線ベクトル\(\vec {n_{\pi}}=(-1,2,1)\)
平面ρの法線ベクトル\(\vec{n_{ρ}}=(-2,1,-1)\)
(二)求めた2つの法線ベクトルの内積を使ってcosθを求める
$$cosθ=\frac {(-1)(-2)+2\cdot 1+1\cdot (-1)}{\sqrt {1^{2}+2^{2}+1^{2}} \sqrt {2^{2}+1^{2}+1^{2}}}$$
$$=\frac {3}{6}=\frac{1}{2}$$
(三)cosθに対応するθを答えとする。
(※:cosθに対応した有名角の求め方については、「三角方程式の解き方(の単位円の部分)」で解説しています。)
ここで、cosθ=1/2 を満たすθの値は60°のみ。
したがって法線ベクトルのなす角=2平面のなす角=60°・・・(答)
対称点の座標を求める【京大過去問】
では、この記事(法線ベクトルの利用)の総まとめの問題を解いていきましょう。
座標空間に4点A(2,1,0),B(1,0,1),C(0,1,2),D(1,3,7)がある。
3点A,B,Cを通る平面に関して、点Dと対称な点をEとするとき、点Eの座標を求めよ。
(2006 京大)
<解説>せっかくなので、これまで学習してきた外積を利用してみます。
解き方の順番
1:ベクトルAB,ACを求める
2:ベクトルABとACの外積を使って平面の法線ベクトルを求める
3:求める点Eと点Dの中点をHとおいて、点Hが平面上にある事を利用する。
4:OE=OD+2DH が成り立つので、(3)で求めた点Hを代入してEの座標を求める
解答解説
問題文より、点A,B,Cが同一平面上にある(平面αとします)ので、\(\overrightarrow {AB} と\overrightarrow {AC}\) を求め→\(\overrightarrow {AB}×\overrightarrow {AC} =\vec {n}\)
(\(\vec {n}\)は平面αの法線ベクトル)。だから、
$$,\overrightarrow{AB}=(-1,-1,1), \overrightarrow {AC}=(-2,0,2)$$より、このベクトルの外積を成分表示すると、(2,0,2)。
したがって、法線ベクトルの一つは(2,0,2)=(1,0,1)。
よって、この平面αの方程式はx+z+d=0・・・(1),
平面α上の点C(0,1,2)を代入してd=-2。(1)のdが-2と分かったので、この平面αの方程式は、x+z-2=0・・・(2)
ここで、平面α上にある「点H」はベクトルを使って\(\overrightarrow {OH}=\overrightarrow{OD}+t \vec {n}\) と書けるので
(1,3,7)+(t,0,t)=(1+t,3,7+t)。これが(2)を満たすから、(1+t)+(7+t)-2=0
よって、t=-3。tを(1+t,3,7+t):(←点Hの座標)に代入し、
\(\vec{OH}=\vec {H}=(-2,3,4)\)
最後に、点Eを\(\overrightarrow {OE}=\overrightarrow {OD}+2\overrightarrow{DH}\)として計算すると、
\((1,3,7)+2(-3,0,-3)=(-5,3,1)\)
よって、平面に関して対称な点Eの座標は(-5,3,1)・・・(答)
まとめと空間ベクトルシリーズ
・法線ベクトルは主に3通りの方法で求めることができる
・なす角の問題=法線ベクトル&内積の利用
・なす角や対称点の問題以外にも法線ベクトルを利用する問題・分野は色々とあるので、次回以降さらに紹介していきます。
・今回解説した「法線ベクトル」(や関連する線形代数学)の考えは、『機械学習』の「分類」で活用されるなど今後ますます重要性が高まっていきます。AIなどに興味がある人は、「線形代数の入門シリーズ」とともに「高校数学ではじめる機械学習シリーズ」も読んでみてください!
空間ベクトルの応用(平面・球面の方程式の記事一覧)
・第一回:「平面の方程式の求め方とその応用」
・第二回:「球面の方程式の求め方と練習問題」
・第三回:「2球面が重なってできる円や、球の接平面の方程式の求め方」
・第四回:「今ここです」
ベクトル全体のまとめ記事
今回もご覧いただき有難うございました。
当サイト「スマホで学ぶサイト、スマナビング!」は
わからない分野や、解説してほしい記事のリクエストをお待ちしています。
また、ご質問・誤植がございましたら、コメント欄にお寄せください。
記事が役に立ちましたら、snsでいいね!やシェアのご協力お願いします
・その他のお問い合わせ/ご依頼は、ページ上部のお問い合わせページよりお願い致します。

