熱化学を0から学べるシリーズ5~問題の解き方&比熱~
さて、シリーズ第1回(「熱化学の導入(1)」)、から、前回の第4回までで、
熱化学方程式とエネルギー図について学んできました。
今回はそれらを用いて「エネルギー図を用いる方法」と、「熱化学方程式の消去法」、の2通りの方法で実際に問題を解いてみることにします。(問題は随時追加していきます。)
目次(タップした所へ飛びます)
ヘスの法則とは
まず、熱化学の熱量を求める問題を解くとき、大前提となるのがヘスの法則です。
~ヘスの法則の意味~
化学反応の反応熱は反応前後の状態のみによって決まり、反応経路によらず一定である。
例えば下の図においてはQ = Q1 - Q2となります。
この「ヘスの法則」を用いることで、Q,Q1,Q2のうち、2つが分かっていれば残りの1つを求める事ができます。
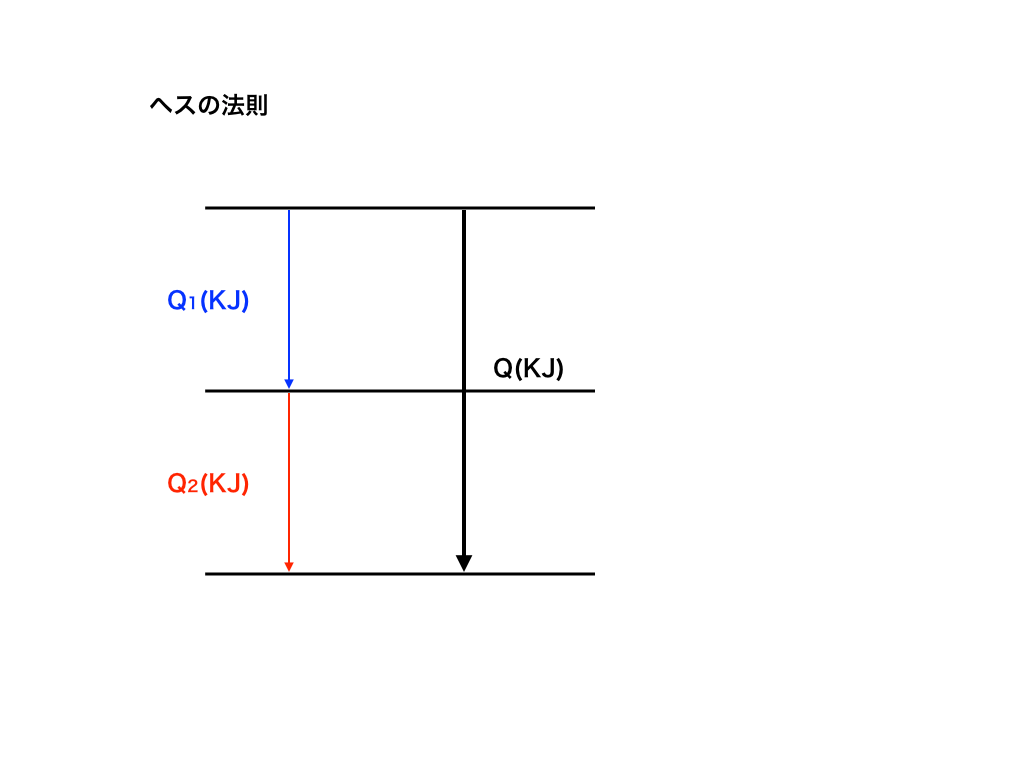
<ヘスの法則とエネルギー図>
この法則をもとにして様々な問題を解いていきましょう!
エネルギー図を用いて問題を解く手順
反応熱を求める問題が出た時に、まず選択するのがここで紹介する【エネルギー図を使う方法】です。
基本的に方程式が3つ以上あれば、この方法を使うと考えてよいでしょう。
以下の2つのステップで図を書いていきます。
手順1.:問題文中の「○○熱」、「△△エネルギー」を確認し、エネルギー図を描く準備をする
手順1の熱とエネルギーの種類、矢印をどこからどこまで書くのかについては
→<第4回;「6種類の熱と3種類のエネルギーのfromとto,基準となる物質をまとめて解説」>を参考にしてください。
それをもとに(陽イオン)→原子→(陰イオン)→単体→化合物→完全燃焼→水和物の6(陽・陰イオンを含めると七)つの状態の中から、図に書く必要がある状態を選択します。
(例)
問題文に「生成熱」が含まれている。→単体・化合物が必要
〃に「電子親和力」が含まれている→原子(気体)と陰イオンが必要 など・・・
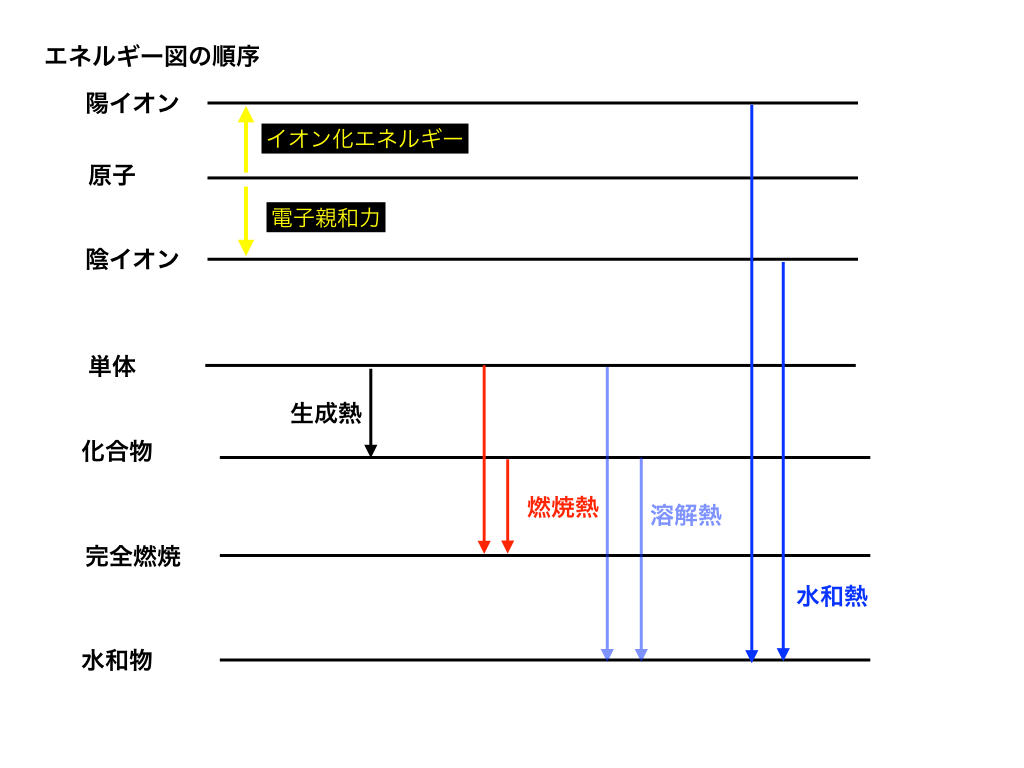
(参考:エネルギー図での”各々の状態の位置”と”熱・エネルギー”)詳しくは、先ほどのリンクで解説しています。
手順2: 1で選択した状態をもとにエネルギー図を書いていく。
(実際の描き方・解き方はこの記事の<問題>のところで紹介します)
といったような手順で問題を解いていきます。
この解法は慣れないと難しい解法なので、ここで一つ図の描き方と、問題の解き方の一つを紹介します。
自信のある方はぜひ自分でチャレンジしてから続きを読んでみてください。
<問題>
以下の条件を用いて塩化ナトリウムの生成熱を求めよ。
(1)ナトリウムの昇華熱は109(kJ/mol)である。
(2)塩化ナトリウムの格子エネルギーは782.5(kJ/mol)である。
(3)塩素の結合エネルギーは243(kJ/mol)である。
(4)塩素の電子親和力は356(kJ/mol)である。
(5)ナトリウムの第1イオン化エネルギーは498(kJ/mol)である。
<解答>
(1)~(5)の条件を考えて、エネルギー図を描くにあたって必要な状態を確認し、図を描いていきましょう。
エネルギー図は以下のような形となります。
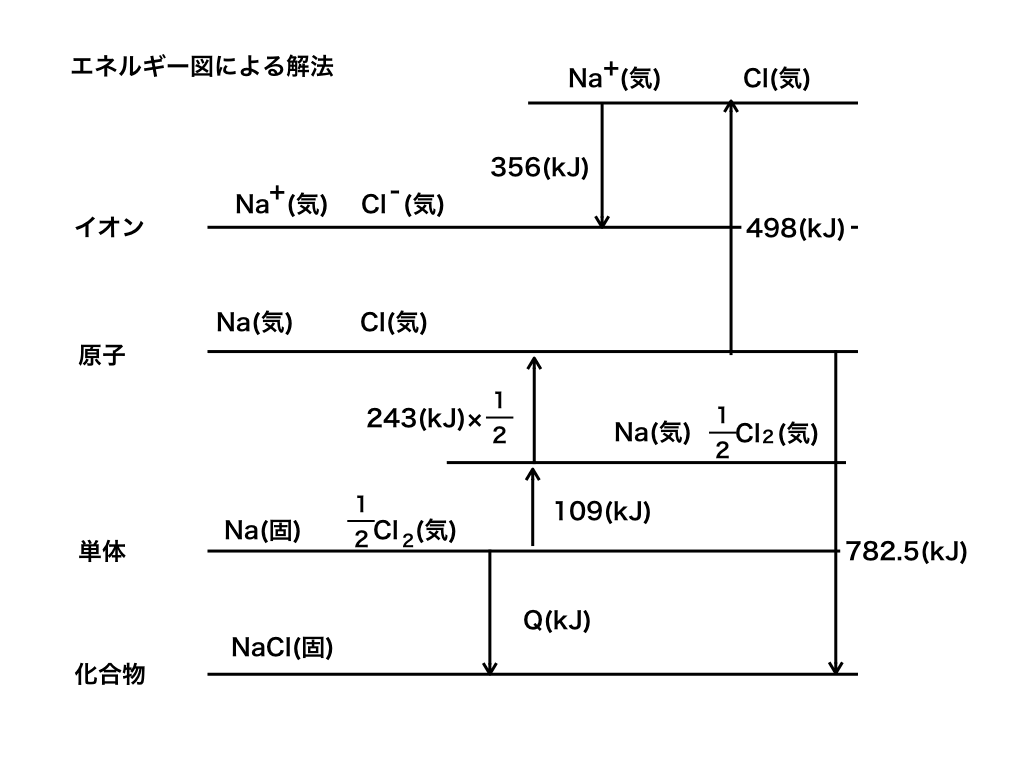
<塩化ナトリウムの生成熱を求めるための図>
しかしながら、今回エネルギー図を描こうとして、どうしても先ほどの6つのステージに当てはめることができなかったという方も少なくないのではないでしょうか。
特に今回の問題で難しいのが、昇華熱、電子親和力、第1イオン化エネルギーの処理です。
このような場合、イオン→→水和物、までの6つのステージ”だけ”にとらわれすぎず、自分で新たなステージを作り出すことによって、エネルギー図をわかりやすくするという工夫が必要になります。
(慣れてくると、わざわざこのようなステージを図に書き込まなくとも、いくつかの熱やエネルギーをまとめて考えることによって6つのステージで完結する図を描くことができるようはなります。)
しかし、最初のうちはこのように自分でわかりやすいような工夫をして図を描くのが確実です。
さて、本題に戻りましょう。上記のように図を描くことができたので、最後は計算です。以下のような立式によってQを求めます。
Q + 109 + 243/2 + 498 - 356 = 782.5 ∴Q = 410(kJ/mol)
したがって、塩化ナトリウムの生成熱は、410(kJ/mol)・・・(答)であると求まります。
今回の問題は前回の記事でお話した各エネルギー・熱のおさらいとしてもちょうど良いかと思います。
ぜひ自力で解けるようにしておきましょう。
消去法を使って問題を解く手順
反応熱を求める問題の中でも、難易度の低い単純な問題であれば、エネルギー図を用いるよりも消去法で解く方が早いこともあります。方法は以下の通りです。
手順1: 求める熱をQ (kJ) として、熱化学方程式の完成した式を書く。
手順2: 問題文の条件をそれぞれの熱化学方程式に書き起こしていく。
手順3:手順 2で書いた式を連立し、不要な物質を消去することでQを求める。
消去法の注意点
色々な問題を解いてみるとわかってくるのですが、この解法は連立式が多いと消去するのも難しくなります。
あくまでも消去法は”一部の簡単な問題においてのみ”使用するもので、”基本的にはエネルギー図を使う”ということを抑えておきましょう。
ちなみに、以下で紹介する、<問題2>は消去法の方が結果的には早く解けますが、
このような簡単な問題の場合でも、普段(テストの時などスピードを要求されない時)はエネルギー図を用いた解法で解くことができるように練習することをオススメします。
何故なら、エネルギー図で解く方法をマスターするのは大変ですが、単純な問題で練習しておくことによって、徐々に複雑な問題であっても対応できるようになってくるからです。
(比較用)問題2:黒鉛と一酸化炭素の燃焼熱からCOの生成熱を求める問題
問1:C(黒鉛)の燃焼熱は394(kJ/mol)、CO(気)の燃焼熱は283(kJ/mol)である。このとき一酸化炭素の生成熱を求めよ。
エネルギー図を用いて解く方法
問題文中に「生成熱」と「燃焼熱」の記述があるので、
→「単体」、「化合物」、「完全燃焼」の段階をエネルギー図に記す必要があることがわかります。
これをもとにエネルギー図を書くと以下の図ようになります。
・まず、黒鉛の燃焼熱より、単体の位置にのC(黒鉛)とO2(気)をおき、
完全燃焼の状態まで(黒色↓)を下向きに394(kJ)を書き込み、CO2(気)を一番下に配置します。
・次に、CO(気)の燃焼熱が与えられているので、化合物であるCO(気)が完全燃焼してCO2(気)となることを次のようにしてエネルギー図に書き込みます。
化合物「CO(気),1/2O2(気)」から(赤色↓)を下(完全燃焼)へ283(kJ)書き込みます。
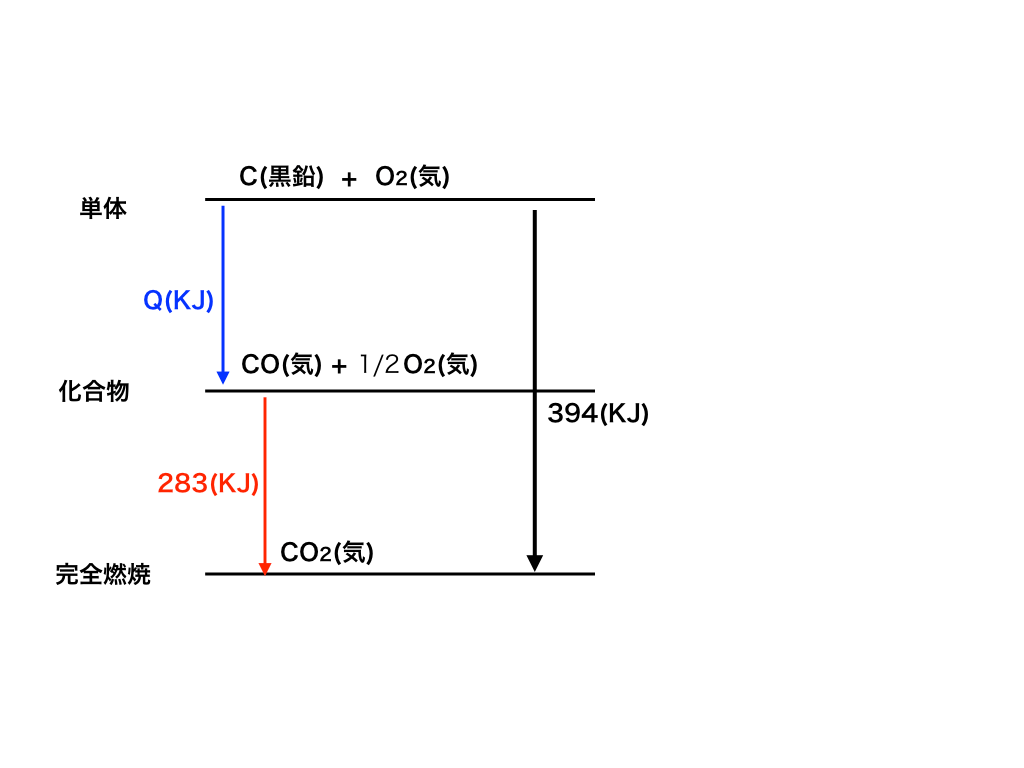
あとは、単純に「黒色の↓」マイナス「赤色の↓」をすれば、
求めたい青色の↓(COの生成熱)がも止まるので、生成熱は394 - 283 = 111 (kJ) ・・・(答)。
消去法で解く
~要求されている(完成した)熱化学方程式を先に書きます~
C(黒鉛) + 1/2O2(気) = CO(気) + Q (kJ) ・・・(1)
~与えられている条件から作った熱化学方程式を連立します~
C(黒鉛)+ O2(気) = CO2(気) + 394 (kJ) ・・・(2)
CO(気)+ 1/2O2(気)= CO2(気) + 283 (kJ) ・・・(3)
(1)式を見ると、(2)式と(3)式から、CO2(気)を消去すればQが求まるということがわかります。よって、(2)ー(3)より、Q = 394 - 283 = 111(kJ/mol)・・・(答)
比熱・熱容量計算
熱化学では、ここまでで紹介してきた”熱化学方程式”や”エネルギー図”がメインに扱われますが、忘れてはならないのが比熱・熱容量計算です。
また、この比熱・熱容量は冷却曲線(溶液の分野)などと融合して出題される事が多いので、合わせてチェックしておきましょう。→「冷却曲線と水の状態変化がわかる!」
比熱とは?
物質1gもしくは1molを1K上昇させるのに必要な熱量のこと。
単位は「J / g・K」もしくは「J / mol・K」となる。
問題によって単位が異なるので、注意して問題文を読む必要があります。
単位を見ても分かる通り、比熱に『物質量(mol)、あるいは質量(g)』と温度上昇度(K)をかけ合わせると、必要な熱量が求まります。
Q(熱量:単位J)=Δt(温度変化:単位ケルビンK)×n(物質量:単位mol)×c(比熱:単位J / mol・K)
あるいは、Q=Δt×m(質量:単位g)×c(比熱:単位J/g・K)
熱容量とは?(比熱との違いに要注意)
溶液の入った容器を1K温度上昇させるのに必要な熱量のこと。単位はJ / Kとなる。
つまり、熱容量(Cで表される事が多い)に上昇温度を掛け合わせると、必要な熱量が求まります。
Q(J)=Δt(単位K)×C(J/K)
今回のまとめと熱化学シリーズ一覧
・熱化学の反応熱を求める問題ではエネルギー図を用いた解法を第1選択とすること
・エネルギー図は慣れの部分が大きいので、類題を探して量をこなすこと
・比熱cとは物質1g、もしくは、1molを1K温度上昇させるのに必要な熱量のことであり、単位は「J / g・K」もしくは「J / mol・K」
・熱容量Cは、溶液の入った容器を1K温度上昇させるのに必要な熱量のことであり、単位はJ / K
・状態変化など、溶液分野も合わせてチェックしておく。
熱化学を0から学ぶ!シリーズ一覧
第1回:「熱化学シリーズ〜イントロダクション〜」
第2回:「熱化学方程式と化学反応式の違い」
第3回:「エネルギー図の書き方と5つの知識」
第4回:「エネルギー図の状態と計9種類の熱・エネルギーを徹底解説」
第5回:「(今ここです)」
第6回:「現在作成中(熱量を求める問題演習アラカルト:詳細な解説付き)」
今回も最後までご覧いただき、ありがとうございました。
「スマナビング!」では皆さんのご意見/ご質問/記事のリクエストを募集しております!ございましたらぜひコメント欄にお寄せください。
SNSで、B!やいいね!シェア、公式Twitterのfollowをしていただけると助かります。

