ベクトルの外積って何?
ベクトルについて勉強していると、「内積」というベクトル同士の掛け算が登場します。
そこからの自然な考え方として、「内」積があるのだから、「外」積もあるのでは?と思う人も多いのではないでしょうか?
当然「外積」も存在するのですが、現在高校では教えられていません。
ただし、外積を理解しておくと数学(特に、空間ベクトルの「平面の方程式での法線ベクトルの利用」など)
や、物理(特に電磁気学)などで理解が進むこともあるので、
意欲でハイレベルを目指す高校生や、
大学の理系学部1年生で線形代数学を学び始めた(る)方にも役に立つ内容になっています。
(線形代数学のシリーズは現在作成中です)ので、ぜひこの記事を読んでみてください。
目次(タップした所へ飛びます)
外積とは何か?
※ベクトルの内積は既知のものとして進めるので、曖昧な人は
・「ベクトルの成分表示での内積と、垂直条件、平行条件」を先にご覧ください。
内積と外積の共通点と相違点
$$内積は\vec {a}\cdot \vec {b}$$
の様に表し、この時、ベクトルとベクトルの間を(・)で表すので、ドット積と言ったりもしました。
一方で、$$外積は\vec {a}× \vec {b} $$
と表します。
スカラーの掛け算と同じ様に(× )を使うので、クロス積とも言います。
重要なことは、
内積が(ベクトル量)・(ベクトル量)=スカラー量
になるのに対して、
外積は(ベクトル量)× (ベクトル量)=ベクトル量 となることです。
つまり、外積の答えは「向き」と「大きさ」の”2つの情報を持っている”ということが出来ます。
外積の順番
次はかけ算の順番についてです。
詳しくは現在制作中の線形代数の記事で解説しますが、
外積はその順序が変わることで答えが変化します。
つまり、なす角θ =0°,180° の時を例外として、
$$\vec {a}\times \vec {b} ≠\vec {b}\times \vec {a}$$
となるのです!$$内積は\vec {a}\cdot \vec {b} =\vec {b}\cdot \vec {a}でしたし、$$
普通のスカラー量同士のかけ算、例えば2×10=10×2の様に答えは変わらなかったことを考えると、
かなり異なっていることがわかると思います。(理由は後述します。)
外積の大きさの意味するもの
さて、外積の答えは「大きさ」と「向き」の情報を持つベクトル量だと説明しました。
では、ここでの「大きさ」とは何を表しているのでしょうか?
二つのベクトルが作る平面
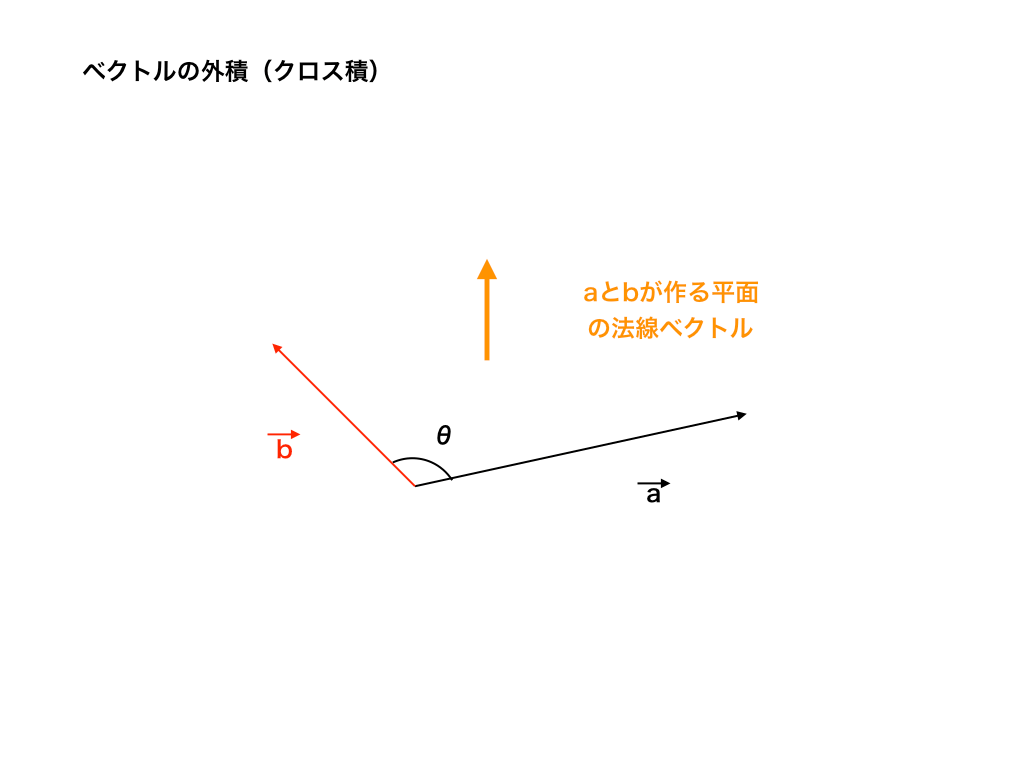
<2つのベクトルがはる平面>
その為には、二つのベクトルが作る平面を理解する事が大切です。
$$今、空間中にある\vec{a} と、\vec{b} $$
が作る平面(なす角θ)は平行四辺形になります。
外積の大きさ
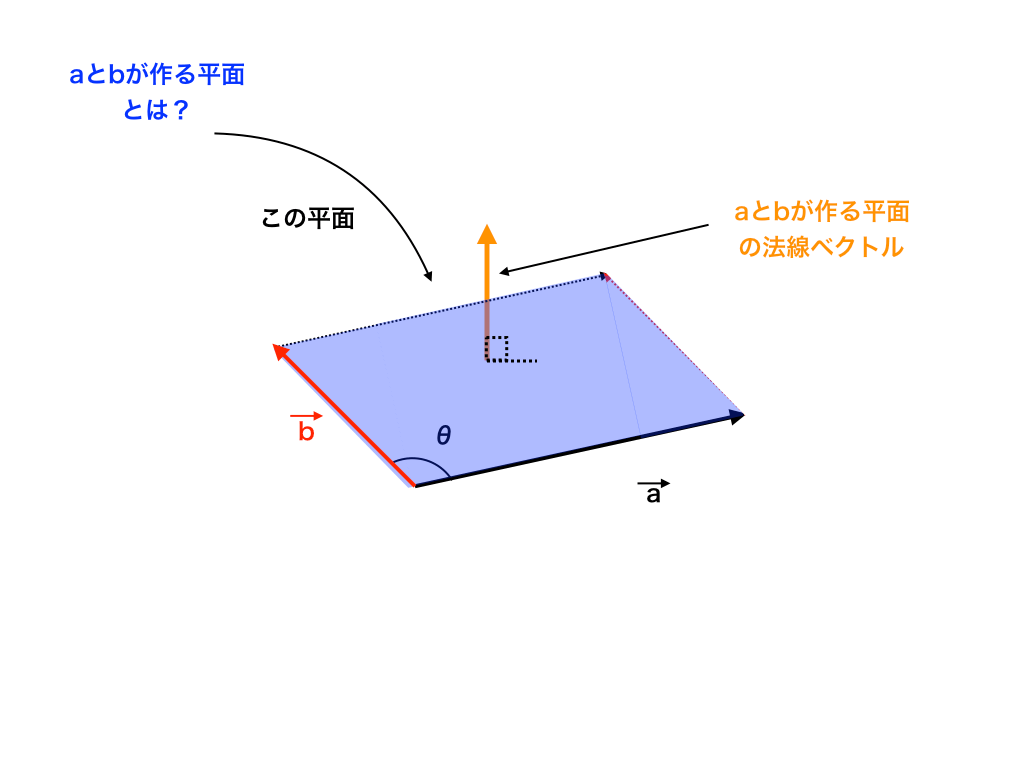
<図2:外積の大きさ(平行四辺形の面積)>
そして、この平行四辺形の面積(Sとします)こそが、$$\vec{a} \times \vec{b} $$
の“外積の大きさ”になります。
これを式で書くと、
$$S=|\vec{a}|\cdot|\vec{b}|sin\theta$$
となります。以下の<図3>参照
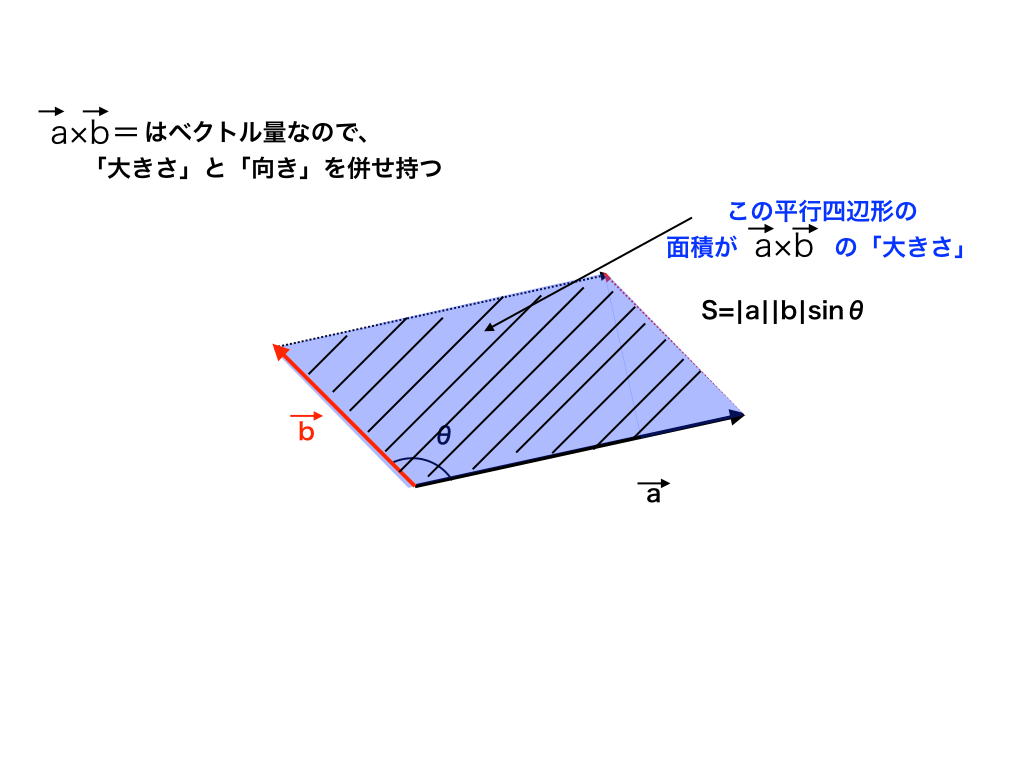
<図3:外積の大きさと平行四辺形の面積>
外積の向きの求め方
大きさの求め方が分かったかと思うので、次に「外積の向き」について見ていきます。
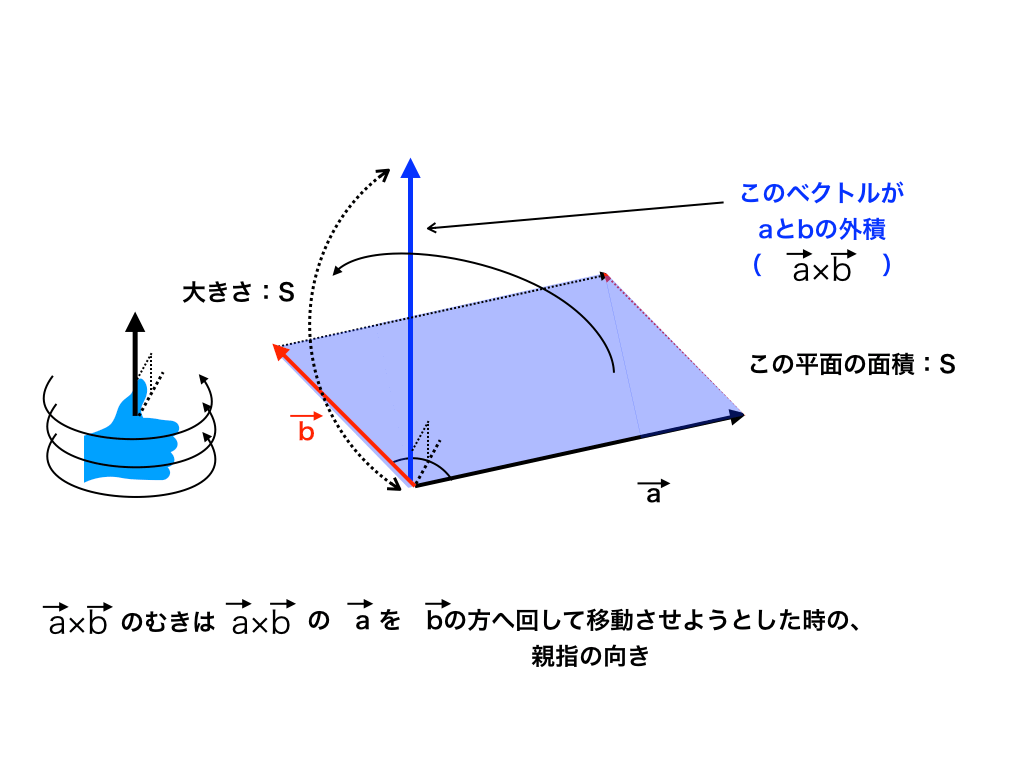
<図4:外積の向き(右ねじの法則)>
この向きの決め方が少しヤヤコシイのですが、ベクトルAを、ベクトルBまで回して重ねる様に、
右手の親指以外を<図4左下>の要領で丸めた時の親指の向きが、
$$\vec{a} × \vec{b}$$の向きになります。
(分かりにくい人は、高校物理の磁気分野で、【電流が作る磁界の方向を決める】ときと同じだと考えてみて下さい。)
結局、ベクトルの外積は薄い青色の平面(ベクトルAとベクトルBが作る平面)と垂直な、青のベクトルであると言えます。
順序の違いで外積が変わる理由
先ほど、外積は普通順序が変わると結果も変わる性質があると書きました。
その理由を上の<図4>で考えてみると、
$$\vec{a} × \vec{b}から\vec{b} × \vec{a}$$
に順序が変わることで、AベクトルからBベクトルに向かって回す方向が逆になります。
つまり、親指の向きは下になることから、外積は真逆を向くことになるのでかける順番によって結果が変化するのです。
成分表示での外積
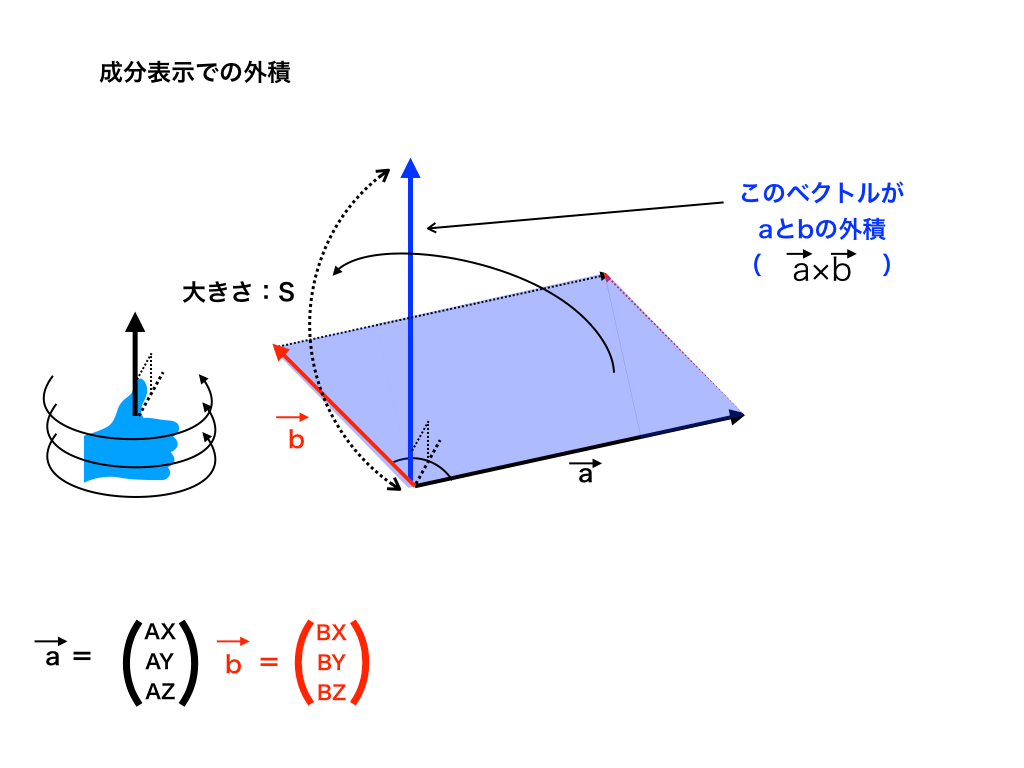
<成分表示での外積>
以上でキソ的なベクトルの外積の解説はほぼ終わったのですが、もうひとつ学ぶ事があります。
それは、ベクトルの成分表示されたベクトル同士の外積の大きさです。
成分表示での内積の場合は、(a,b,c)・ (p,q,r)=ap+bq+cr (スカラー量)でした。
外積の場合はもう少し複雑で、
$$\vec{a}=\begin{pmatrix}
Ax \\
Ay \\
Az
\end{pmatrix} ,\vec{b}= \begin{pmatrix}
Bx \\
By \\
Bz
\end{pmatrix},$$の成分で表されるとき
$$\vec{a} × \vec{b}=\begin{pmatrix}
AyBz-AzBy \\
AzBx-AxBz \\
AxBy-AyBx
\end{pmatrix}$$
という成分で表されたベクトル量 になることに注意して下さい。
外積のまとめと平面の方程式、線形代数へ
さて、今回はベクトル同士の掛け算のうち「外積」を学んできました。
外積と平面の方程式
かける順番で結果が異なる事など、これまでの算数・数学と違う部分があり戸惑った方もいるかもしれません。
しかし、外積は『線形代数』という学問の入り口になるだけでなく、
高校数学においても、『法線ベクトル』を求める際に大変役に立つので、
難関大を目指す受験生の方にもぜひ知っておいてもらいたい内容です。
>>「平面の方程式と外積を使って求めた法線ベクトルの利用」<<
〜線形代数へ〜
また、主に行列を扱う線型代数学の入門講座を作ったので、興味のある方はぜひ以下の記事をご覧ください。
↓(線形代数シリーズ制作中)↓
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
「線形代数学入門(2):行列同士の掛け算の仕方をイラストで解説」
(↓ベクトルに関する記事のまとめです↓)
今回も最後までご覧いただき有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNS上での反応を参考に日々改善・記事の追加更新を行なっています。
そこで
・記事リクエストと質問・ご意見はコメント欄にお寄せください。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為にぜひご協力お願いします!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

