指数・対数とは?基本的な意味と指数/対数方程式の解き方

指数方程式・対数方程式をマスター

・この記事を読むべき人：指数・対数の知識があいまい〜指数方程式・対数方程式の問題が解けない人

・到達目標：指数対数の計算・法則のマスターと基本〜標準レベルの指数・対数方程式が自力で解ける

・記事の構成：指数法則と公式→指数方程式→対数法則と公式→対数方程式→まとめ

この記事では、数学２で学習する「指数・対数」より、その方程式の解き方を例題を通して習得します。

また、試験の際に見落としがちな「真数条件」などの注意点＋ちょっとした工夫を解説しています。

(2019/01/30追記:続編(指数・対数不等式)が完成しました。)

指数方程式と指数法則

指数方程式は、その名の通り指数で構成された式で未知数を解くことを目的とします。

（例）3^2x+2・3x+1=0の時のxを求める。

その為、指数法則を自由に使いこなせることが前提条件です。

指数・対数における”底”

指数・対数では、この底が重要な意味を持ちます。例えば、３^x では「３」が「底」の指数となります。

対数においても、log₂Aでは、「２」が「底」の対数という言い方をします。

指数法則と関連公式

ここでは、基本的な指数法則・公式を紹介しておきます。

特に理系の人は数３などの極限・微積分で必須なので今のうちに知識を固めておきましょう。

「基本的な指数法則」

A^a×A^b=A^(a+b)

A^a÷A^b=A^(a-b)

(A^a)^b=A^(a×b)

（AB）^a=A^a・B^a

※忘れてしまったり、どちらが足し算か、掛け算か、わからなくなってしまった時は、

底が2や３といった具体的な数字を使って確認すると良いです。

※有名な幾つかのべき乗は覚えておくとよい

２の１０乗＝1024

３の５乗＝243

7の３乗＝343 など・・・

指数方程式の解き方と工夫

指数方程式を具体的な例題を使いながら解いていきましょう。

例題１）３^x＝２７の時のxの値を求めよ

例題２）３^２x＝81の時のxの値を求めよ。

例題３）3^2x-2・3^x+1=0の方程式の解を求めよ。

例題４）9^x-7・３^x＋6＝0の方程式の解を求めよ。

解答

(1)指数xを求める最も基礎の問題です。

3をx乗すると27になるので、3・3・3=27より、x=3

(2)3^2x=81:ここでは指数部分がxでは無く、2xになっています。

指数法則で紹介した、A^bc=A^b(c)を思い出すと、2xは2かけるx→((3の2乗)のx乗)と同じ事なので、

9^x=81。9のx乗が81なので、x=2。

試しに、3^2xのxに2を入れてみると、3⁴=81となり、確かに成立しています、

(3)ここから先、本格的な方程式になってきます。

（２）で３^2x＝(3²)^xとして、問題を解いていきました。

ここでは、3^2x=(3^x)²と考えて方程式を解きます。

どちらも、指数の順番を入れ替えただけなので、同じ値です。

(3^x)²とする理由：これは、方程式を黄色でマークした部分に(3^x)があるからです。

3^2x-2・3^x+1=0 ここで、3^x＝tとおくと、(3^x)²＝t²となるので、

与式＝t²-2t+1=0 と置き換えることができます。

指数を文字で置き換える時の注意

指数は、常に正の値を取ります。xにどんな実数を代入しても以下の図のように、

０に限りなく近づきますが０以下の値をとることはありません。

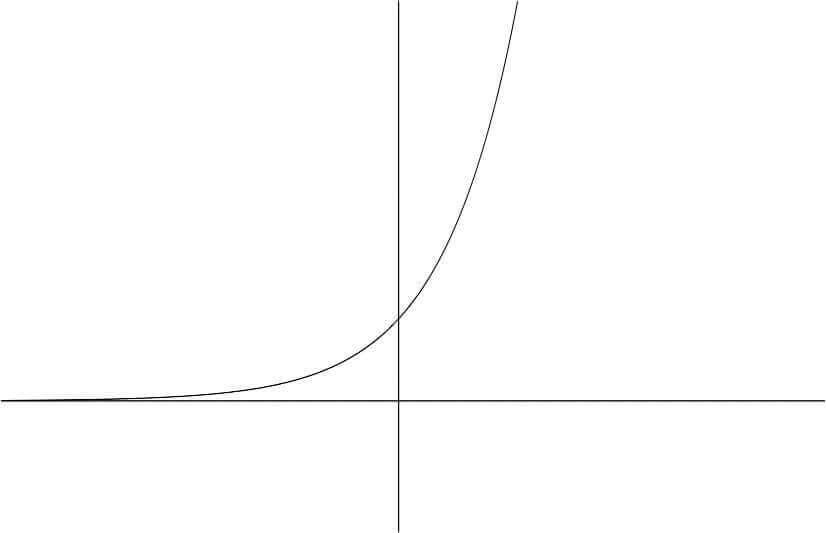
＜指数関数のグラフ例＞

（※従って、上の図と3^x＝tより、tは常に正；t>0の条件がつきます。）

t²-2t+1=0と、t>0より、因数分解して(t-1)²=0,t=1

3^x＝tだったので、3^x＝1従ってx＝０・・・（答）

(4)問４は、9^x-7・３^x＋6＝0の方程式です。

底である数が、"９","３"と揃っていないので、"９"を小さいほうの"３"に揃えることにします。

9=3²より、9^x=(3²)^x ＝(3^x)²とすることができます。（やっていることは問３と同じです）

これで底が揃ったので、(3^x)²ー7•３^x＋6＝0 を再び３^x=tと置いて解いていくと、

t²-7t+6=0,(t>0) 因数分解して、

(t-6)(t-1)=0,よってt=1,6。

したがって、3^x=1,6、xの解のうち3x=1→x=0は理解できるかと思います。

・・・しかし、3^x=6となる数を思いつくでしょうか？

『３をx乗すると６になる』xはこれまでの数学では表すことができそうにありません。

そこで、これから学ぶ『対数log』の考え方が重要になります。

（先に『３をx乗すると６になる』xの答えを書いておくと、”x=log₃6”となります。が、

？？だと思うので、続きの対数方程式と対数の注意点をご覧ください。

対数方程式と対数の注意点

対数について。

例）log_aB=C :この式の右辺＝log_aBのaを「底」、Bを「真数」と呼び、これが＝Cとなっている時、

aをC乗したらBになる数のことをC=log_aBと表します。

例えば、log₃81=4 ：この対数は、確かに3を4乗したら81になることを示しています。

では、なぜわざわざこのような表記をするのでしょう？

先ほどの問４の解答を思い出してもらえればわかると思いますが、

上のlog₃81のように、対数の値がきれいな整数や分数で表すことができれば良いのですが、大抵の場合そうならないからです。

3を○乗したら６になった。この時の○の値は簡単には表すことができませんね。

このような時、○＝log₃６という風に、logを使うことで簡潔にできるのです。

対数法則と関連公式

ここからは、対数の法則を見ていきます。

底が同じ（揃っている）場合、対数の足し算は真数のかけ算。

log_aB+log_aC=log_aBC

同様に、対数の引き算は真数の割り算。

log_aB-log_aC=log_aB/C

真数の○乗はlogの前に出すことができる。

log_aB^m =m・log_aB

＊最重要：「底」の変換公式

上三つのような便利な性質を利用するには、「底」が同じでなければいけませんでした。

そこで、底が異なる対数を同じ底に変換してしまうのがこの公式です。

log_xy=log_ay/log_ax

揃えたい底（ここではa）の対数の真数に、元の対数の底（x）と真数（y）を使ってlog_axとlog_ayを作り

分母にlog_ax（元の対数の底）分子にlog_ay（元の対数の真数）を配置した分数で表すことができます。

対数の底と真数の条件

ここで、対数を扱うときに必ず守らないといけない条件があります。

それが、真数条件と底の条件です。

まず、対数の底が０より大きく１でないこと。

次に、真数が０より大きいこと。

log_(底)(真数)とすると、底＞０かつ底≠１。真数＞０

底が特別な値をとる対数

詳しくは各記事で説明していますが、対数の中には底の値が「１０」や、

「e：（ネイピア数；e≒2.718・・・）」であるものがあります。

これらの対数のことを特別に、常用対数（底＝１０の時）、自然対数（底＝eの時）という名前がついています。

常用対数は１０進法と相性が良く、桁数などを求める際によく使います

＜参考：「常用対数の意味と利用（桁数・最高位の数）」＞。

自然対数は、底であるネイピア数の関数e^xが微分してもe^xであることから、

＜「ネイピア数eの正体とは」＞、

数学３の対数微分法を始めとしてあらゆることに利用されています。

＜「対数微分法とは？やり方を解説」＞

対数方程式の解き方と工夫

対数方程式とは、その名の通り対数（log）が入った方程式です。

こちらも例題を見ながら解き方・注意点などを習得していきましょう。

（例題１）log₆216=x

（例題２）log₂(x+2)+log₂(x+5)=2

（例題３）(log₂x)²+2log₂x=8

解答編

（解答１）対数の性質が理解できていればすぐ解ける問題です。

６をx乗したら216になるので、216＝6³ よって、x=3

(解答２)この式では、真数が（x＋２）と（x＋５）になっています。

真数は常に＞０なので、x＋２＞0かつ、x＋５＞０より、x＞−２（真数条件）

左辺の対数の底が２でそろっているので、”右辺の２”も底が２の対数で表しすと、

２＝log₂2²  ←まずlog₂2=1です。さらに、

真数の２乗を対数の前に出すと２log₂2=2となるので、全て底を２に揃えた式にして整理すると、

log₂(x+2)+log₂(x+5)＝log₂2²

ここで、真数に注目して(x+2)(x+5)=2²

x²+7x+10-4=0

(x+1)(x+6)=0

したがって、x＝-1,-6

ここで、真数条件x＞-2より、x＝-1・・・（答）

この問題のポイントは右辺の２を対数で表すところです。

（解答３）問３では、対数log₂xそのものが２乗されています。

このような式の場合は、(log₂x)=tと文字で置き換えて解いていきます。

（与式）⇔t²+2t-8=0

(t-4)(t+2)=0と因数分解できるので、t＝４,-2

真数条件x＞０に注意して、

log₂x=4,-2より、xは２を４乗した数と、同じく２を−２乗した数になるので

2⁴=16,2^-2=1/4 これはx＞０を満たす。

よって、x＝16,1/4・・・（答）となります。

指数対数のまとめと続編はこちらから

・指数・対数方程式の基礎を学びましたが、このほかにも指数・対数不等式やその応用など、いろいろな問題が出題されます。（続編作成中）

・底と真数条件に注意

・底を揃えることを考える

続編:指数不等式、対数不等式 +相加相乗平均の解説記事ができました。以下のリンクより続けてご覧ください。

・【NEW！】:「指数・対数不等式と相加・相乗平均」

対数・方程式の関連記事

＜対数の関連記事：「常用対数を使って桁数や最高位の数を求める方法」＞

以下の記事で様々な方程式・不等式の解き方を網羅しています

＞＞「高校数学での方程式/不等式の解法総まとめ」＜＜

最後までご覧いただきまして、有難うございました。

・当サイト「スマナビング！」では読者の皆さんからの記事のリクエスト、ご質問・ご意見をお待ちしています。ぜひコメント欄にお寄せください。

・ また、snsでいいね！やシェア、B！、Twitterのフォローをしていただけると助かります。

・その他のお問い合わせ/ご依頼ほかに付きましては、お問い合わせページよりお願い致します。