確率変数の期待値/分散/標準偏差
<この記事の内容>:確率変数の『期待値』:E[X]・分散:V[X]・標準偏差:D[X]の計算の仕方、さらに線形性などの重要な性質をまとめました。
(随時更新・証明追加中)
目次(タップした所へ飛びます)
期待値Eとは
期待値を求める際に、E[X]やE(X)を用いて表します。
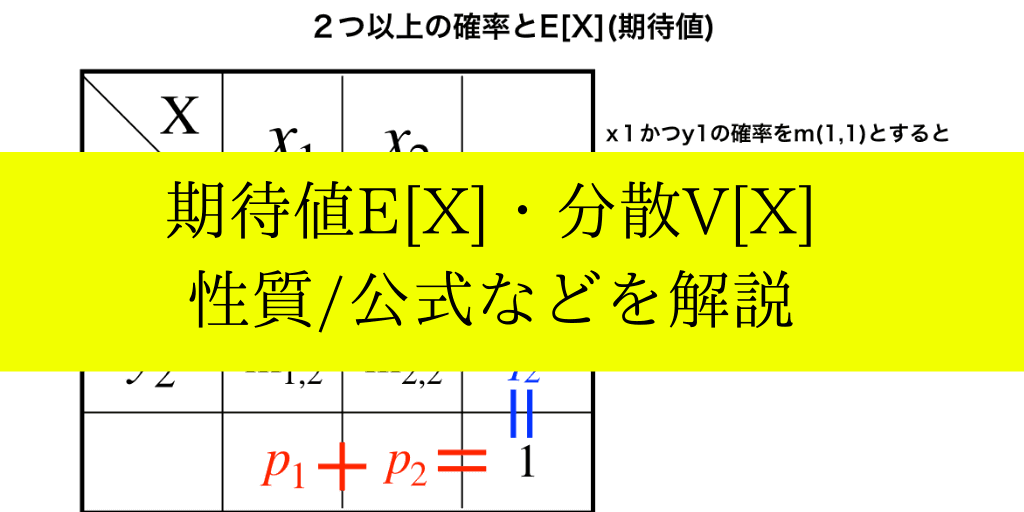
期待値:E(X)の定義
データの平均と異なって、確率変数の場合は”期待値”と呼びます。
$$E[X]=\sum_{k=1}^{n}x_{k}\cdot p_{k}$$
\(P(X=x_{k}\))の離散型の確率分布での期待値は、上の式のように計算します。
また、一般的にE(X)はμ(ミュー)で表すことが多いです。
連続確率分布での期待値
$$\mathrm{E[X]}=\int_{-\infty}^{\infty}x\cdot f(x)dx $$
「連続確率分布と離散確率分布」で扱ったように、連続型の確率分布は『Σの代わりに積分』で考えるので、定義の式も上のようになります。
分散V(X)の定義とE
$$V[X]=\sum_{k=1}^{n}(x_{k}-μ)^{2}$$
分散・標準偏差は基本的に「データの分析(2)」で扱っている『データの分散・標準偏差』と同じ考え方で求めることができます。
すなわち、各確率から期待値(平均値)を引いたものの2乗をk=1~nまで総和すれば良いのです。
また、先ほどのμのように分散は\(σ^{2}\):シグマの小文字(ギリシャ文字:Σが大文字、σが小文字)の2乗で表記します。
\(\mathrm{V[aX+b]=a^{2}V[X]}\)
\(\mathrm{V[X]=E[X^{2}]-E[X]^{2}}\)
標準偏差D(X)
\(D[X]=\sqrt{σ^{2}}\)
標準偏差も同様で、上で求めたV[X]のルートを取ることで求まります。
したがって、D[X]=σと書けます。
標準化と”Z”
こちらも「データの変量変換」で扱った、『標準化』の確率変数バージョンです。(正規分布の記事で利用します。)
$$\mathrm{E[Z]=\frac{X-μ}{σ^{2}}}$$
性質も、変換後の期待値=0、分散=1と同じで証明方法もほとんど共通しています。
E (X)やV(X)の公式
以前→「データの平均・分散・標準偏差の変数変換」において、『データ』の変量変換の式とその証明を紹介しました。今回は、『確率変数』の場合の公式を見ていきます。
期待値Eの公式
・\(\mathrm{E[aX+b]=aE[X]+b}\)
上の式の証明を簡単に載せておきます。
$$E[aX+b]=a\sum_{k=1}^{n}x_{k}p_{k}+b\sum_{k=1}^{n}p_{k}$$
ここで、\(p_{1}+p_{2}+\cdots +p_{n}=1 \)なので、\(b\sum_{k=1}^{n}p_{k}=b\cdot 1=b\)
ゆえに、\(\mathrm{E[aX+b]=aE[X]+b}\)
以降の式も同様にすることで証明可能なので、データの変量変換の記事などを見ながらご自身で導いてみてください。
同時確率(複数の確率変数)でのEとV
\(\mathrm{E[X+Y]=E[X]+E[Y]}\)
\(\mathrm{E[X+Y+Z]=E[X]+E[Y]+E[Z]}\)
\(\mathrm{E[X_{1}+X_{2}+\cdots +X_{n}]}\)
\(\mathrm{=E[X_{1}]+E[X_{2}]+\cdots +E[X_{n}]}\)
特に上の式については、【積率母関数】のところなど様々な場面で利用するので、説明を付け加えておきます。
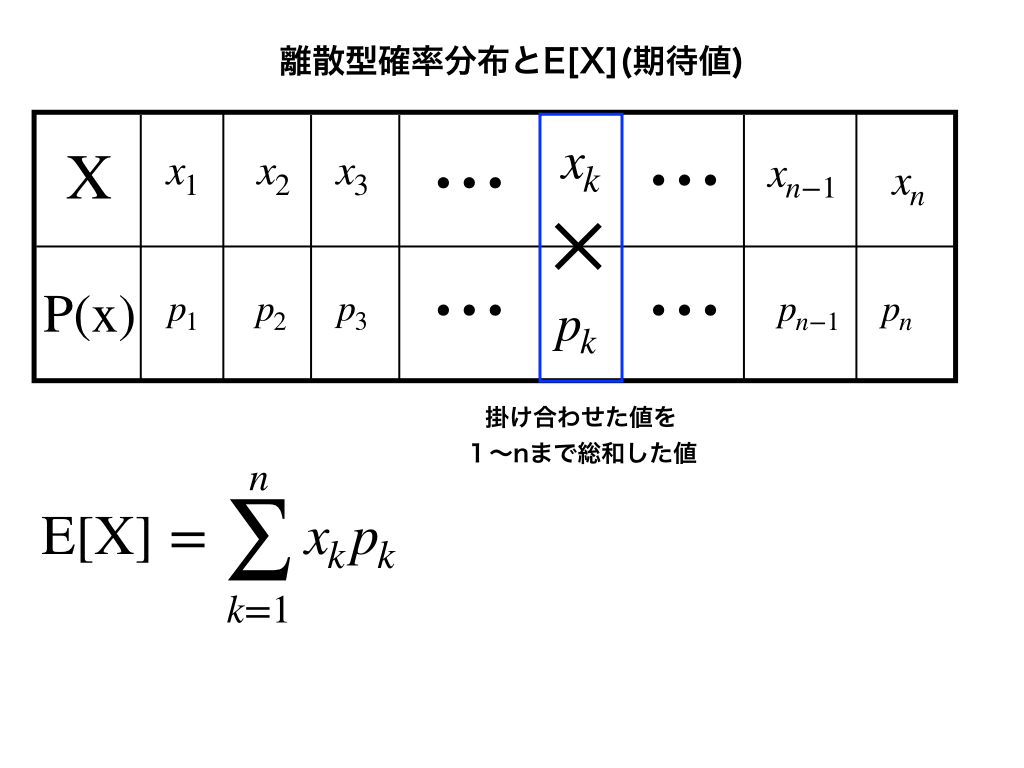
今、上の図のように2つの確率分布表があり、それぞれの確率変数が
\(X=x{1},x_{2}\)
\(Y=y_{1},y_{2}\)
という小さな場合で考えてみます。
(X,Y)の組み合わせは2種類×2種類の4種類となるので、2つの表を合わせてみましょう。
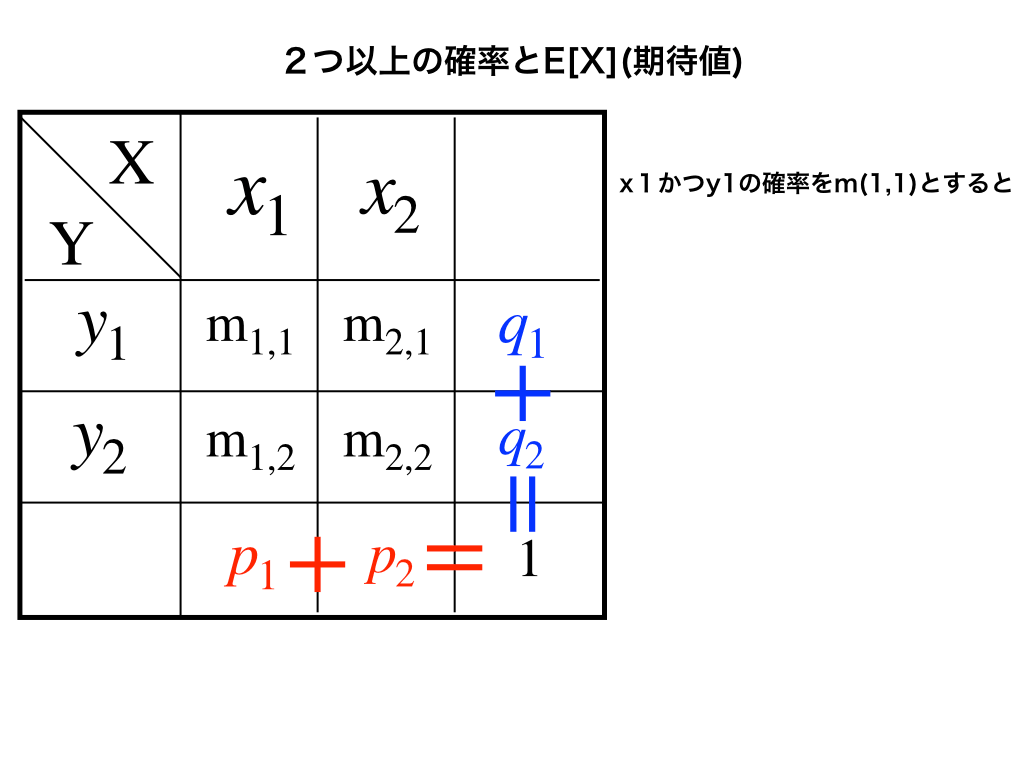
\(x_{1}かつy_{1}の確率をm_{1,1}\)のように表すと、\(m_{1,1}~m_{2,2}\)までの4通りの確率を足したものが1となります。
ここで、
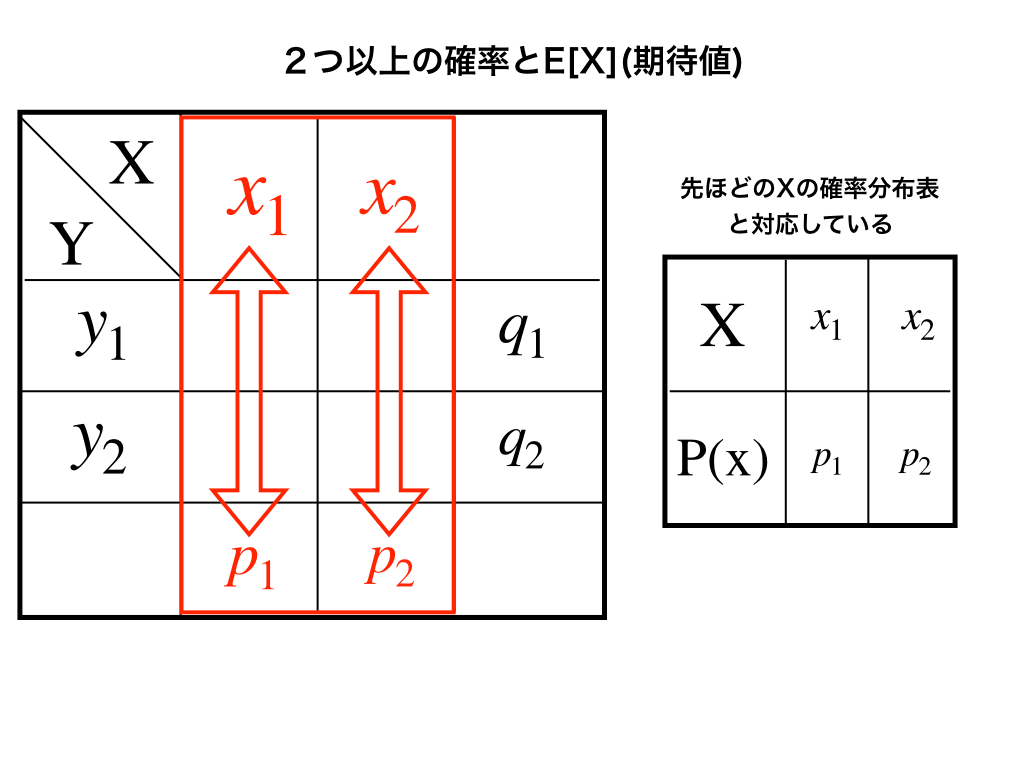
(図2)
※下の図右のコメントは「Xの確率分布表と〜」ではなく→「Yの確率分布表と〜」です。
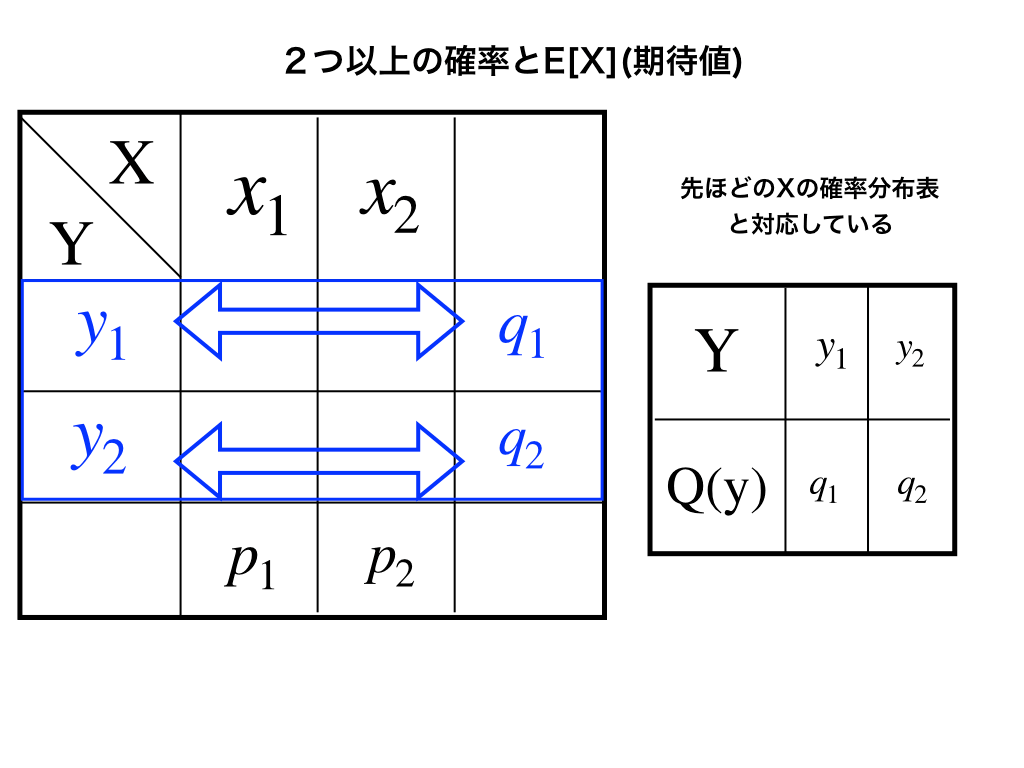
のように、確率が対応しているので、
\(E[X+Y]=(x_{1}+y_{1})\cdot m_{1,1}+(x_{1}+y_{2})\cdot m_{1,2}\)
\(+(x_{2}+y_{1})\cdot m_{2,1}+(x_{2}+y_{2})\cdot m_{2,2}\)
上の式を展開して、
\(=x_{1}m_{1,1}+y_{1}m_{1,1}+x_{1}m_{1,2}+y_{2}m_{1,2}\)
\(+x_{2}m_{2,1}+y_{1}m_{2,1}+x_{2}m_{2,2}+y_{2}m_{2,2}\)
この式を整理していきます。x,yでそれぞれくくると
\(x_{1}(m_{1,1}+m_{1,2})+x_{2}(m_{2,1}+m_{2,2})=x_{1}p_{1}+x_{2}p_{2}\)
\(y_{1}(m_{1,1}+m_{2,1})+y_{2}(m_{1,2}+m_{2,2})=y_{1}q_{1}+y_{2}q_{2}\)
となって、それぞれ$$\sum_{k=1}^{2}x_{k}p_{k}=E[X],\sum_{k=1}^{2}x_{k}p_{k}=E[Y]$$
の定義式になっているので、
E[X+Y]=E[X]+E[Y]
となります。
これはx、yの数や、確率変数の数にかかわらず成り立つので、
例えばE[X+ aY+Z]のような場合でもこの考え方で対応できます。
(この場合、E[X+ aY+Z]=E[X]+ aE[Y]+E[Z]となる)
なお、
\(\mathrm{E[XY]=E[X]・E[Y]}\)という”積の”関係は、XとYが独立に起きる場合にのみ成立する点に注意が必要です!
同時確率での分散V
ここでの分散の公式は”それぞれの確率変数が独立の場合”にのみ成り立ちます。
\(V[X+Y]=V[X]+V[Y]\)
もちろん
\(V[X_{1}+X_{2}+\cdots +X_{n}]\)
\(=V[X_{1}]+V[X_{2}]+\cdots V[X_{n}]\)
も成立します。
まとめと今回の応用記事へ
・今回紹介したE[X]、V[X]の式や性質は今後どんどん使っていくので、証明や仕組みも含めて早めに理解して覚えておきましょう。
統計学一覧
次回:「ベルヌーイ試行と分布・二項分布へ」
これまでの記事は以下↓のページでご覧いただけます。
最後までご覧いただきまして、有難うございました。
【総合学習メディア】:「スマナビング!」では、読者の皆様からのご感想を募集しています
(※:個々の問題・証明の質問等には、対応出来ない場合があります)
また、お役に立ちましたら、SNS等でシェアして頂ければ幸いです。
・その他の「お問い合わせ/ご依頼/タイアップ」等に付きましては、【運営元ページ】よりご連絡下さい。