ロジスティック方程式とシグモイド関数
<高校数学で始める機械学習のコラム>
今回は、機械学習の中でもニューラルネットワーク (NN)の活性化関数として良く利用される『シグモイド関数(曲線)』について、その関数とロジスティック方程式という(はじめは人口や個体数を予測する数理モデルであった)微分方程式との関係を紹介していきたいと思います。
目次(タップした所へ飛びます)
シグモイド関数(曲線)とロジスティック関数
機械学習を学んでいると、ニューラルネットワークで、いきなり”シグモイド関数”なるものが現れて、戸惑っているの方も多いのではないでしょうか。
三角関数や対数関数はまだ何となく馴染みがあるかと思いますが、高校でも”シグモイド関数”など習いませんでした。
$$\varsigma_{(x)}=\frac {1}{1+e^{-ax}}$$
実は「(標準)シグモイド関数」は、人口を予測するとある微分方程式(ロジスティック方程式)から導き出すことができるのです。
マルサスの「人口論」
1798年にイギリス人のトマス・マルサスが一本の論文を世に出しました。
そこには、人口が激増する時代が来ると予測して、それを微分方程式を使って説明していました。
<微分方程式については→「微分方程式の基礎と色々な分野への応用」で簡単に紹介しています。>
マルサスの微分方程式(人口の予測)
彼の論文によれば、人口をy、時間をtとして
\(dy/dt=ay\) の式で表せるとあります。
これはいわゆる「変数分離型」の微分方程式で、微分方程式の中でも最も簡単な(高校数学Ⅲ:『積分法の応用』の発展事項でも教えられている)タイプです。
この微分方程式を解くと、
⇔$$\int \frac{1}{y}dy=\int a dt$$
⇔\(\log_{e}y=at +Const (Constは積分定数)\)
⇔\( e^{at +Const}=y、ゆえに、 e^ {at}・ e^{Const}=y\)
ここで e^Cは、定数(ネイピア数)の定数乗(Cは積分定数)より定数Aと置けます。
e^C=Aと置くと
\(y=A\cdot e^ {at}\)
すなわち、マルサスは人口が時間"t"に連れて指数関数的に増えていくと予測したのです。
もしその予測が正しいならば、マルサスの考えでは人口は無限大に大きくなりますが、
これまでの歴史でその様な事態は起った事は当然ありません。
また、住環境や資源不足など様々な原因でいつか人口は頭打ちになるはずです。
実際、戦後の日本を見ると人口の増加率は急上昇した後、頭打ちになっています。(更に今では人口減少社会になっています)
人口論への疑問とフェルフルストの微分方程式
この様な事を19世紀初頭にすでに予測し、新たな人口増加モデルを考案した人物がいました。
1838年、ちょうどマルサスが人口論を発表した40年後に、ベルギー人の数学者“フェルフルスト”がより現実的な人口モデルを表す微分方程式を発表します。
フェルフルストの微分方程式とロジスティック方程式
フェルフルストが考案した微分方程式は、以下の様に表されます。
この微分方程式を「ロジスティック方程式」と呼びます。
少し難しそうな名前の文字が並んでいますが、ここではシグモイド関数の導出を目指すので深くは触れません。
簡単に紹介しておくと、(右辺)=が時間当たりの人口=人口増加数、
(左辺)の式の意味は、人口増加に伴って、食糧などの環境が追いつかなくなり、個体数(人口)が徐々に増えずらくなっていく様子を(1-N/K)で表したものです。
この微分方程式も変数分離形(先ほどのマルサスモデルと同様です)で解くことができるので、計算をすすめます。
シグモイド関数をロジスティック方程式から導く
さて、この項ではなるべく式変形を省略せず丁寧にロジスティック方程式を解いていく様子を、1〜4までのステップに分けて順番に解説していきます。
1:変数分離によってNとtを両辺に分ける
左辺に集まっているdN・dtを”分離”させます。
$$\frac{dN}{dt}=aN(1-\frac{N}{K})=a(\frac{N(K-N)}{K})$$
まず上の式を”変数分離”します。(つまりNの式をdNへ、それ以外をdtのある右辺へ移動させます。)
$$\frac{K}{N(N-K)}dN=a dt$$
2:部分分数分解の後両辺を積分する
左辺を積分するために、分数の積を分数の和に分解します。
参考:「部分分数分解のやり方と例を解説」
$$\int (\frac{1}{K-N}+\frac{1}{N})dN=\int a dt$$
分解した分数を含む両辺を積分し、
$$-\log{|K-N|}+\log{|N|}=at+Const.$$
対数の定義より、eを(at+積分定数)乗したものが(N/K-N)であるので、
$$e^{at+Const}=\frac{N}{K-N}$$
3:\(t_{0}の時のn_{0}\)を利用し変形する
ここで、t(time)=0の時の人口(個体数)を\(n_{0}\)とおき、上の式に代入すると
$$e^{Const}=\frac{n_{0}}{K-n_{0}}$$
指数法則:\(e^{\alpha+\beta}=e^{\alpha}\cdot e^{\beta}\)を用いて、
$$e^{at}\cdot\frac{n_{0}}{K-n_{0}}=\frac{N}{K-N}$$
4:N=の形にし、パラメーターを調整する
さらに、人口N=の式にしたいので(左辺)にNをまとめるための式変形を行なっていきます。
↑の両辺に(K-N)をかけて(右辺)の分母を払い、N=のカタチにし
$$N=\frac{e^{at}n_{0}K}{K-n_{0}}-N\frac{e^{at}n_{0}}{K-n_{0}}$$
(右辺)の第二項目を(左辺)へ移動した上でNでくくり、
$$N(1+\frac{e^{at}n_{0}}{K-n_{0}})=\frac{e^{at}n_{0}K}{K-n_{0}}$$
今度は左辺の(カッコ)内を通分した上でその逆数を両辺にかけます。(これで左辺はNだけになります)
$$N=\frac{e^{at}n_{0}k}{K-n_{0}+e^{at}n_{0}}$$
ここで、我々はシグモイド関数の形を目指すので、
右辺の分母分子を\(e^{at}n_{0}\)で割ってあげて
$$N=\frac{K}{\frac{K}{e^{at}n_{0}}-\frac{1}{e^{at}}+1}$$
さらに、\(e^{-at}\)でくくります。
$$N=\frac{K}{1+e^{-at}(\frac{K}{n_{0}}-1)}$$
ここでパラメーターの値を、それぞれ,\(n_{0}=K/2,K=1\)とし、timeのtをxにすることで、
$$N=\frac{1}{1+e^{-ax}}$$
ここで、\(N=\varsigma_{x}\)とすると、
$$\varsigma_{x}=\frac{1}{1+e^{-ax}}$$
このようにシグモイド関数を導くことができました。
活性化関数としてのシグモイド関数
ここからは、上で導出したシグモイド関数のグラフや性質・さらにς(x)を微分した結果を見ていきます。
シグモイド関数のグラフ(曲線)と活性化関数
ここまでの過程で求めたロジスティック関数の (パラメーターを一部置き換えた)グラフは次のようになります。
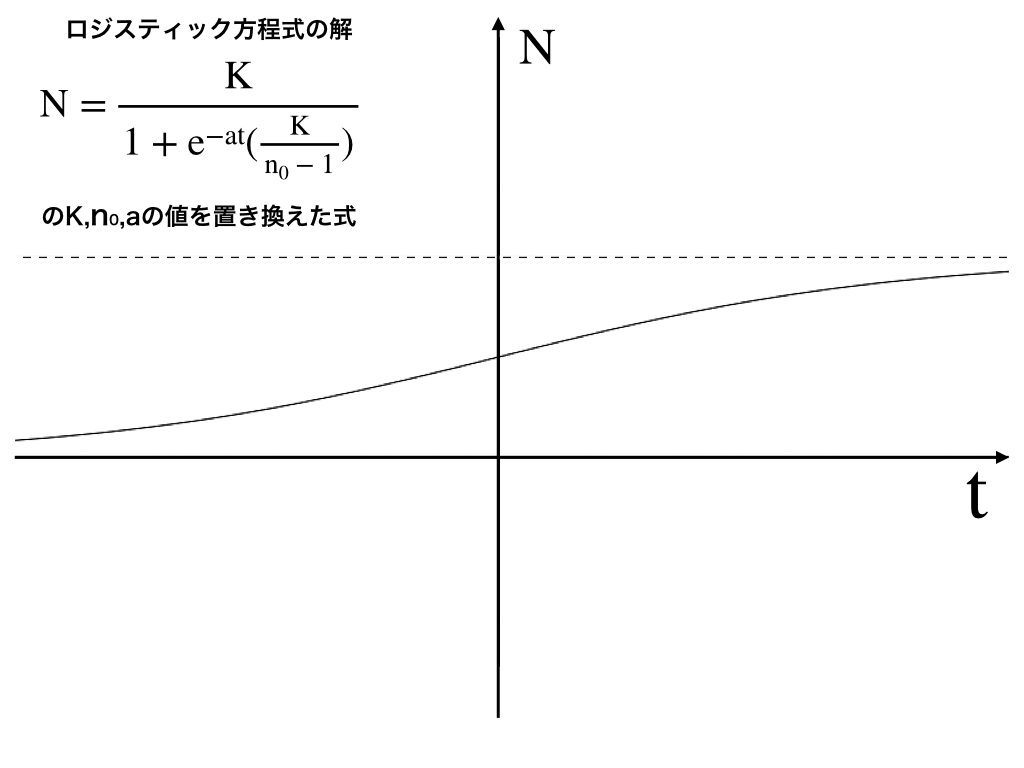
さらにa=1の時、
これを描画したものが以下のようなグラフです。
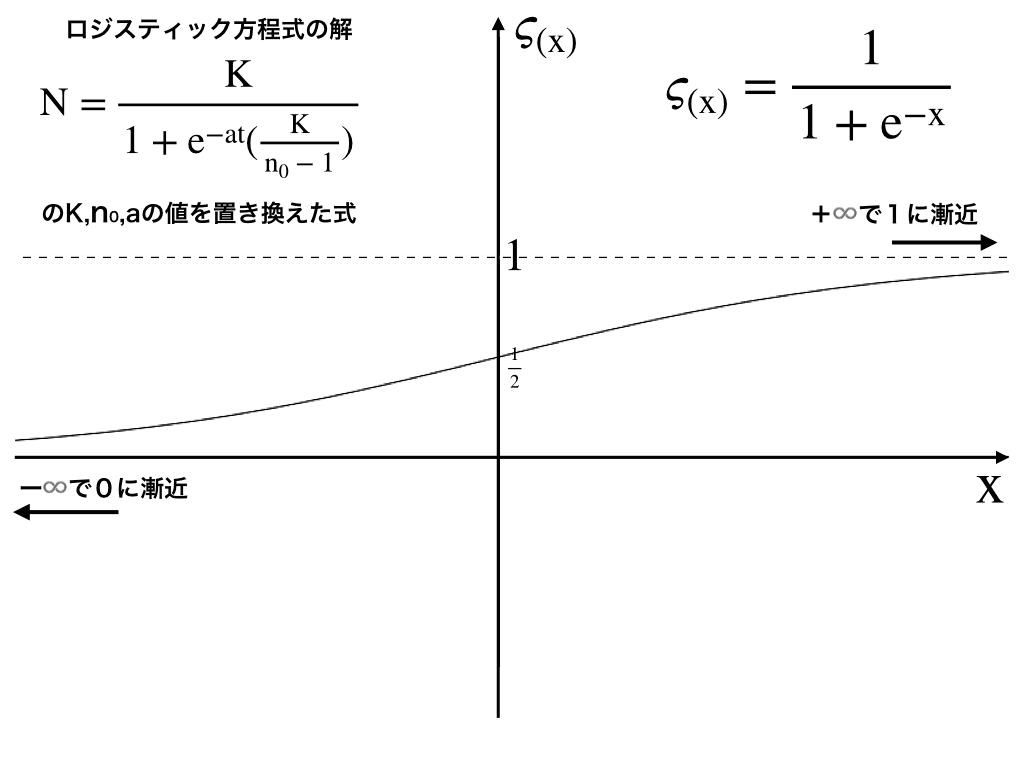
このように、s(ギリシャ文字のς)字型をしているのでシグモイド曲線と呼び、非線形関数であることから、非線形(=直線で区別できない)分類や多層パーセプトロンの活性化関数として使用されます。
シグモイド関数の微分
活性化関数としてシグモイド関数が重宝される点として、微分を行なった結果が同じシグモイド関数をつかって表せる、と言う点があります。
(ネイピア数を底とする指数関数も、この点では同じですね。)
具体的に\(\varsigma(x)\)を微分してみましょう。
$$\varsigma(x)=\frac{1}{1+e^{-x}}$$より、
商の微分法を用いて、
$$\frac{d}{dx}\varsigma(x)=\frac{e^{-x}}{(1+e^{-x})^{2}}=\frac{1}{(1+ e^{-x})}\cdot\frac{e^{-x}}{(1+e^{-x})}$$
ここで、$$\frac{e^{-x}}{(1+e^{-x})}=1-\frac{1}{(1+e^{-x})}$$で表せるから、
\(\varsigma(x)‘=\varsigma(x)(1-\varsigma(x))\)
ついでにもう一度微分してみると(二階微分では、ς(x)の関数のまま合成関数の微分法を用いて計算します。
\(\varsigma(x)''=(\varsigma(x)-\varsigma(x) ^{2})'=\)
\(=\varsigma(x)'-2\varsigma(x)\cdot \varsigma(x)'=\varsigma(x)'(1-2\varsigma(x))\)
ς(x)‘は先ほど求めているので、これを代入することで
\(=\varsigma(x)(1-\varsigma(x))(1-2\varsigma(x))\)
となって、やはりシグモイド関数自身を用いて表すことが可能です。
勾配消失と他の活性化関数
近年では、シグモイド関数が局所解につかまりやすい、傾きが0になる(勾配消失)などの理由で(参考:「最急降下法の仕組みをイラストで解説」)、”ReLU関数”などが主流になっています。
シグモイド関数まとめ
・シグモイド関数はギリシャ文字のς(シグマ)のような形をしていることから名付けられ、
・その非線形なグラフや、シグモイド関数自身の微分がシグモイド関数で表せるといった性質から
・ニューラルネットワークの活性化関数として用いられる。
・”シグモイド”(ςのような形をしている)曲線を表す関数はこの他にもいくつかありますが、今回は『人口・個体数』を表す数理モデルである『ロジスティック方程式』から導出しました。
機械学習・数学コラム・関連記事へ
「(作成予定)ロジスティック関数とロジット関数」
今回も最後までご覧いただき、有難うございました。
総合学習メディア:「スマナビング!」では、読者の皆さんのご感想などの募集を行なっています。
ぜひコメント欄にお寄せください。
B!やシェア、Twitterのフォローをしていただけると励みになります。
・お問い合わせ/ご依頼・タイアップその他につきましては、【運営元ページ】からご連絡下さい。

