
データの分析・(統計学)入門
<このシリーズの対象>データの分析を学習中の学生(主に高校一年〜)と、機械学習などで統計学の知識が必要になった社会人の方
<シリーズの主な内容>数学1「データの分析」を0から始め、『確率分布と統計的な推測』〜記述統計・推計統計まで。
数1データの分析基礎編
今回は、最も基本的なデータの分け方「平均値/最頻値/中央値」と、「四分位数・箱ひげ図の書き方」までを、例をあげながら紹介していきます。
目次(タップした所へ飛びます)
代表値:平均値・最頻値・中央値の意味と求め方
データを表す時最もなじみ深いのが「平均値:アベレージ」だと思います。
しかし、時に平均値は実体を表すのに適切でないと思われる場合があり、その様な時に「最頻値:モード」や「中央値:メジアン」が使われます。
例えば10人の人の中で9人の貯金がゼロであっても、残りの一人が10億円の貯金があれば、この10人の平均貯金額は10億÷10=1億円となります。
数学的には正しいですが、データを分析していくにあたってこれは厄介です。
そこで、「中央値」、「最頻値」が登場します。
具体的に見ていきましょう。
(例)10人の身長を調べた時、それぞれの値は以下の様になった。単位は(cm)。
160、 164、 162、 166、 172、
175、 165、 172、 170、 168
中央値medianとは
データ(今回は10人の身長)を小さい方から大きい方へ並べていったとき、丁度真ん中にあるデータの値をを「中央値(メジアン)」と言います。
しかし、今回は対象となる人数が偶数なので、丁度真ん中に当たる人がいません。
実際並べてみると、
160,162,164,165,166,168,170,172,172,175、
となり、低い方から数えて5人目の人(166cm)と、高い方から数えて5人目の人(168cm)が異なります。
このように、データが偶数(個)の場合は、この二人の身長の平均を「中央値」とします。
$$\frac {(低い方から5番目)+(高い方から5番目)}{2}$$
$$\frac{166+168}{2}=167$$
中央値小まとめ
ここで、一般化してデータの個数を《2n(個)》の場合と《2n+1(個)》の場合(ただし、nは0以上の整数)でまとめておきます。
データの個数が2n(つまり偶数の場合)、n番目とn+1番目の平均を全体の中央値(メジアン)とする。
同様に、2n+1(奇数)の場合、n番目の値を中央値とする。
(ややこしくなったら、n=2や3などを代入して考えてみてください!)
最頻値modeとは
次に、最頻値(mode;モード)とは、文字通り最もデータの数が多い(頻繁に現れる)値のことです。
160、 164 、162、 166、 172、
175、 165、 172、 170、 168
先ほどから扱っている身長のデータを見ると、"172(cm)"が“二人”おり、それ以外の値は全て“一人”なので、このデータの最頻値は172cmとなります。
四分位数と箱ひげ図
では、ここからはデータの分析の基礎となる「四分位数(しぶんいすうと読みます)」および、「箱ひげ図」の作り方を図解します。
四分位数の意味と求め方
まず『四分位数』の意味とその求め方についてです。
データの個数が”奇数”の場合と”偶数”の場合で計算が異なるので、
それぞれの場合についてイラストを使って説明していきます。
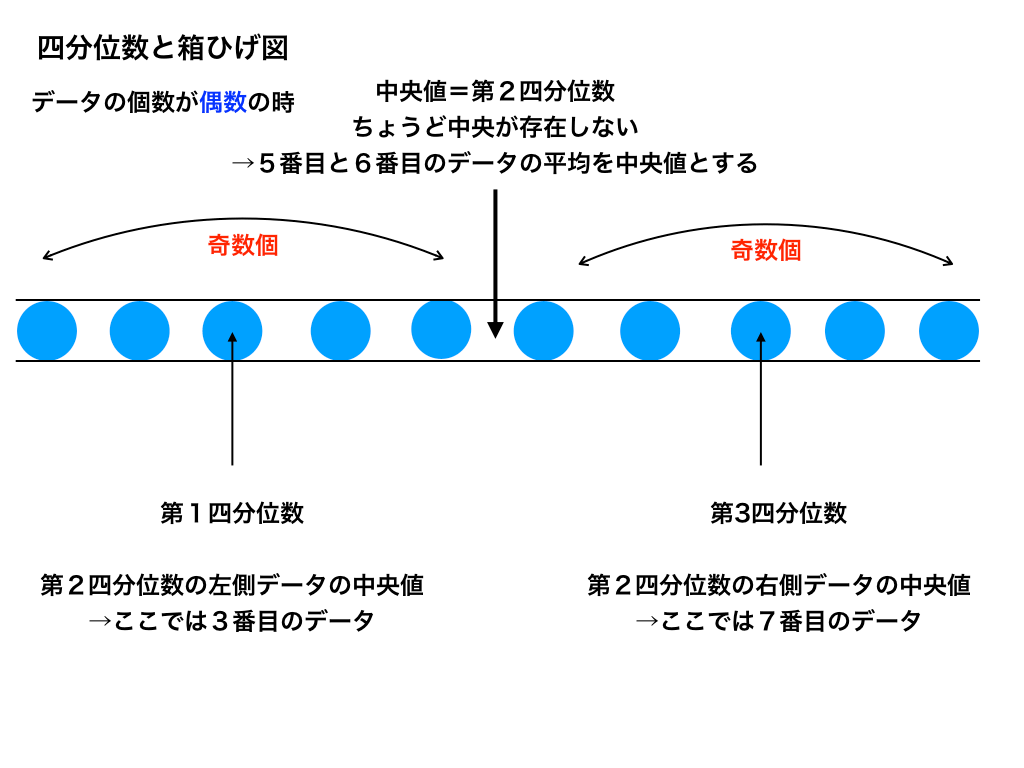
<データが偶数(個)ある場合>
上↑が偶数の場合、下↓が奇数の場合です。それぞれ、どのような所が違うのか確認しながら見ていきましょう。
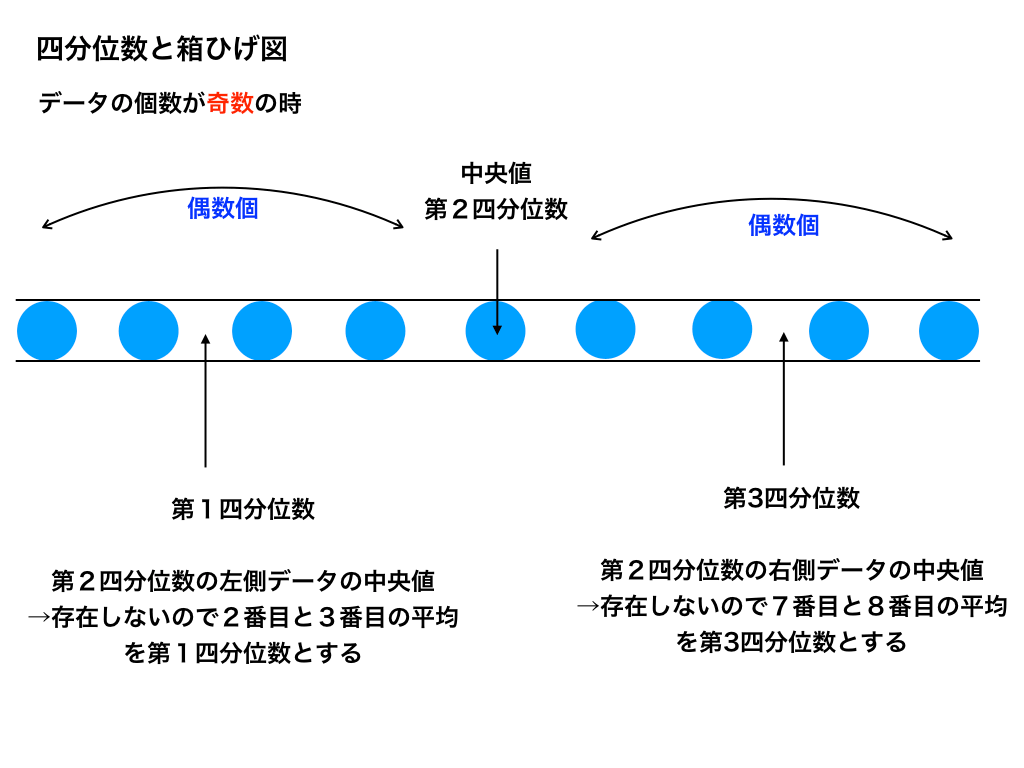
<データが奇数(個)の場合>
第1四分位数とは
第1四分位数は”全体の中央値から最小値までのデータの”中央値となります。
全体のデータが偶数の時は簡単に求まりますが、奇数の時には、本来あるべき場所(上の図では、2番目と3番目)の値の平均値を第1四分位数とすることになります。
第2四分位数とは
第2四分位数は先ほど解説した”中央値”と一致するので理解しやすいと思います。
繰り返しになりますが、データが【偶数個】あるときには、『丁度真ん中にデータが存在しない』ので、『その左右二つの平均値を“第2四分位数”とする』ことだけは注意しておきましょう。
第3四分位数とは
第3四分位数も、第1四分位数の最小値が最大値に変化しただけで、求め方は変化ありません。
データが奇数個の場合に注意すべきことも同じです(図のようにデータの数が9個の時は、7番目と8番目の平均をとる)。
箱ひげ図の作り方
上の項で学んだ第1・第2・第3四分位数と、データの最大・最小値、さらに全データの平均値が用意できれば『箱ひげ図』と呼ばれる図を作成できます。
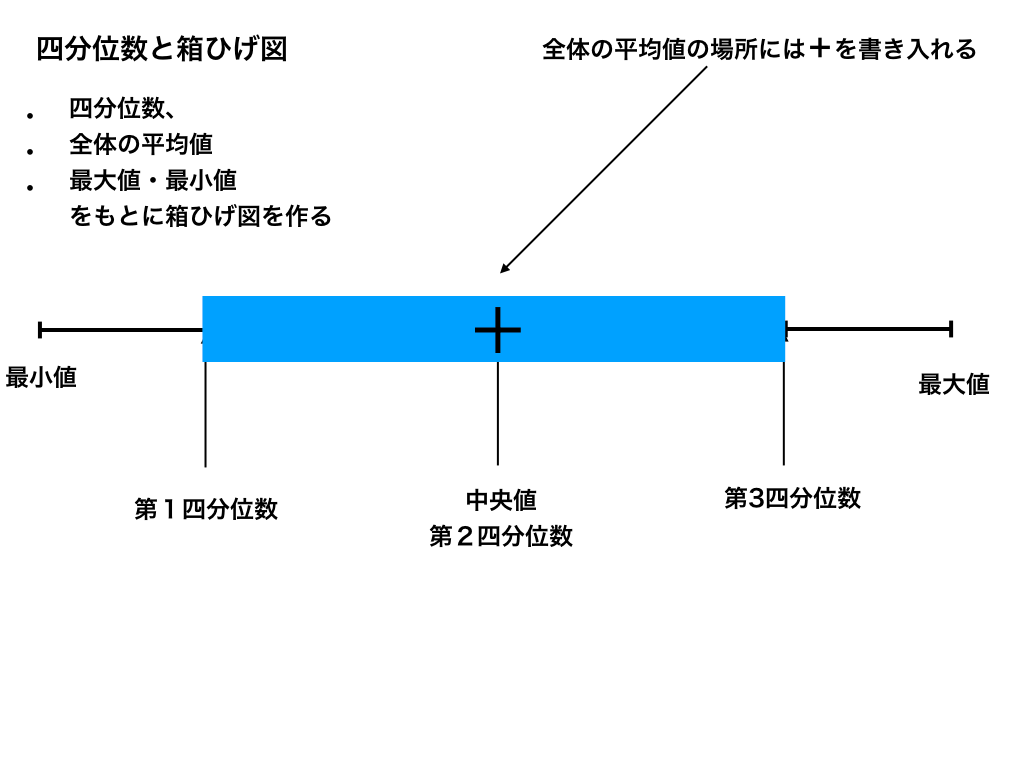
<箱ひげ図の概要>
上の図のように、箱(第1四分位数から第3四分位数の間:『四部位範囲と呼びます』)の部分と、
”ひげのような部分”(:第3四分位数から最大値、と、第1四分位数と最小値の間)を書き込めば『箱ひげ図』はほぼ完成です。
最後に全てのデータの平均値の場所に、『+』の記号を描き入れれば完成です。
上の例では、第2四分位数=中央値と、+:平均値が同じ場所になっていますが、大抵の場合それぞれの値は異なるので、+の位置はもっと右or左の方に書き込むことになります。
範囲と四分位範囲
最小値から最大値までの”ひげ”から”ひげ”までの部分を「範囲」、”箱”の部分を「四分位範囲」と呼びます。
まとめと次回分散/偏差/標準偏差へ
・主なデータの「代表値」のイミと求め方(特に中央値)に注意する
・四分位数では、データの数の偶奇によって求め方が変わる。問題を解いている途中でどちらがどちらかわからなくなったら、5、6個丸を描いて思い出す。
→○○○○○(奇数)○○○○○○(偶数)
・箱ひげ図の『+』:平均値と、中央値の位置関係に注意!
次回は、データの分析の中でも苦手な人が多い『分散』や『偏差』などの計算方法・意味について解説します。
データの分析と確率・統計シリーズ
・第1回:「今ここです」
・第2回:「分散・標準偏差の意味・求め方と計算のコツ」
・第3回:「“2変量データ”の関係を調べる!共分散と相関係数の意味と求め方」
・NEW!:「データの変数変換と標準化を解説」
統計学入門第一回:「統計学とは?学習内容と学ぶ順番」
今回もご覧いただき、有難うございました。 「スマナビング!」では、読者の皆さんのご意見や記事のリクエストの募集を行なっています。
ぜひコメント欄にお寄せください。
snsでB!やシェア、Twitterのフォローをしていただけると励みになります!
・お問い合わせ/ご依頼等に付きましては、【運営元ページ】からご連絡下さい。

