
確率分布と確率変数とは(統計学2)
<この記事の内容>:「統計学とは?0から始める統計入門(1)」の続編として、推測統計学を始め統計学に必要不可欠な『確率分布』と確率変数などの基本的な定義や用語について学んでいきます。
<統計学・データの分析>「統計学シリーズ一覧記事へ」
目次(タップした所へ飛びます)
確率変数とは
確率変数Xとは何か?というところから始めましょう。理解しやすいように、具体例を使って紹介していきます。
(※:それでも初めは用語や定義が少し複雑に感じられるかもしれません。まずはザッとこの記事を読んで、次回以降のさらに具体的な記事「ベルヌーイ分布と二項分布」etc,,,で段々と自然に定着していくので、その頃にまた全体を読み返してもらえれば、と思います。)
確率変数の定義と具体例
今、裏返した1〜K(13)までの13枚のトランプがあるとします。その中から1枚カードを選ぶと、13通りの数字の中から数が定まります。
何らかの試行(トランプを引く)を行ったことにより、その値(1〜13までの値)が定まり、かつ、その値をとる確率(ここでは1/13)が決まっているもののことを言います。
離散型確率分布と連続型確率分布
確率分布には、上で紹介した確率変数によってそれぞれ離散型・連続型という2種類に大きく分けられます。
離散と連続の意味
では連続と離散は何が違うのか、言葉の意味から解説していきます。
・離散が飛び飛びの値を取る事であるのに対して、
・連続はその名の通り値が繋がっています。
サイコロを振ったときの目の値やカードを引いたときそこに書かれている数字などは、1,2,3,・・・と飛び飛びの数を取るので『離散確率変数』です。
が、身長・体重やルーレットが示す値などは『連続型』に当てはまります(どこまでもその値を細かく分けていくことができるからです)。
このように、確率変数・分布には、“離散型”と“連続型”に大きく分けることができます。
離散型確率分布
さらに具体的に、離散型確率分布を見ていきましょう。
先ほどの『確率変数』の項で、”ある値をとる確率が決まっている”と書きました。これを表にしてみます。
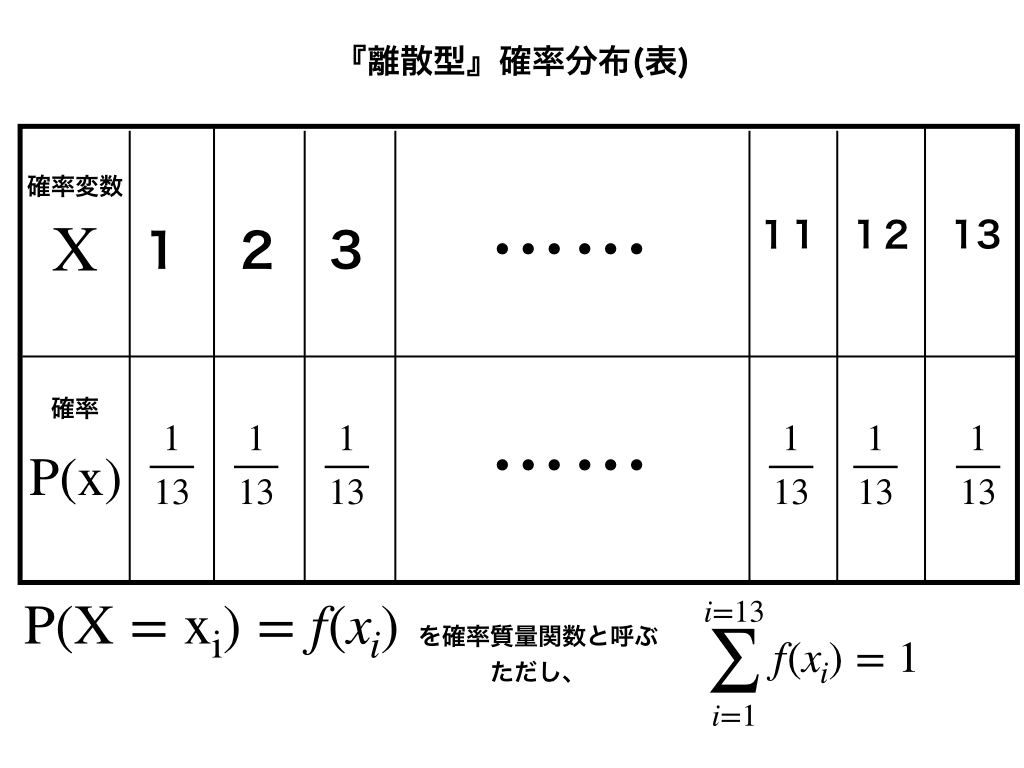
上段のXが引いたカードの値、下段のPがそのカードを引く確率です。
この様に、XとPの対応(の表)を『確率分布(表)』といいます。
・この表全体として確率分布
・上段のXを確率変数
・下段のPを確率
確率質量関数
そして、普通の関数がf(x):【f(x)というハコにx=α(具体的な値)を代入するとf(α)の値を返す】様に、確率変数を入れるとその確率を返してくれるf(x)を確率質量関数と呼びます。
これを一般化すると、
\(f(x_{i})=P(X=x_{i})ただし、\sum_{i}=1\)
(\(X=x_{i}の場合:f(x_{i})\)が確率質量関数で、\(x_{i}\)が全ての値をとる場合その確率の総和「シグマ記号で表しています」が1になる、という意味です)
連続型の確率分布と確率密度関数/一点での確率が0になる訳
続いて、確率変数が連続な『連続型』の確率分布を見ていきます。
いま下の図で例示しているのは”xという値をとる確率f(x)”を縦軸に、”x”を横軸にとったものです。
例として回転する円盤に矢を放つダーツのようなものを考えてみます(ただし必ず円盤に矢が刺さり、外れることがないとする)
そして、刺さった場所の角度0°〜360°を確率変数xとすると、確率分布は以下のように表すことができます。
(初めて連続型の確率分布を学ぶ時に、『「ある一点をとる確率は0」というところが何となく分かりにくい』という人も居るかと思います。そのイメージを下の図で表しました。)
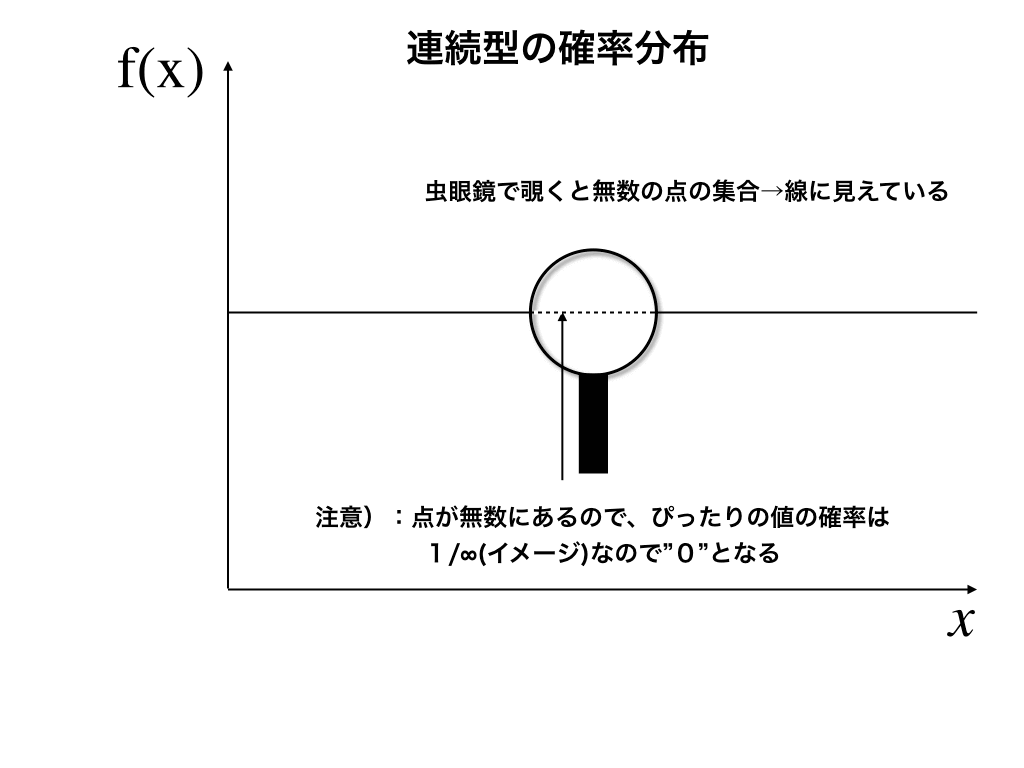
確率密度関数とは
重要なこと:<上・下の図>に書いている通り、連続型はピッタリの値の確率が0になってしまって求めることができないので、その代わりに範囲で確率を考えます。
その際、離散型での”確率質量関数”に相当するのが『確率密度関数』です。
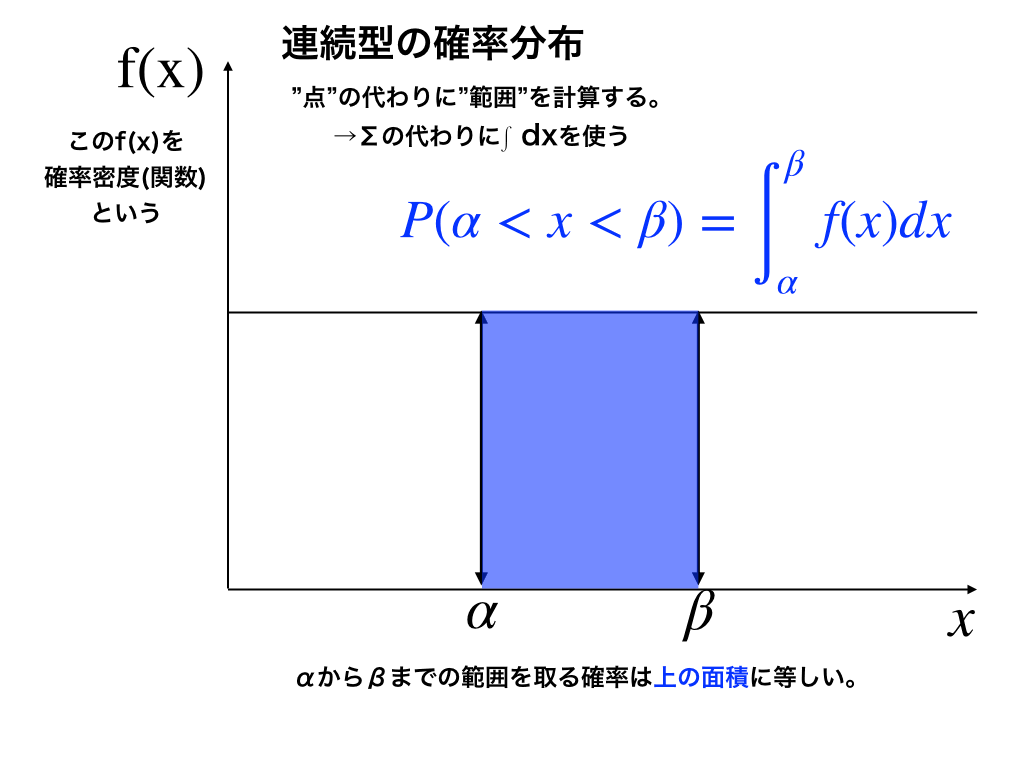
$$\mathrm{P}(\alpha<x<\beta)=\int_{\alpha}^{\beta}f(x) dx$$
上のように、確率密度関数f(x)を求めたい範囲で定積分することにより、その面積=確率が求まります。
さて、ここまでで確率分布・変数や確率関数を大雑把ではありますが紹介しました。
確率分布の種類
確率分布には多数の種類があるので、(離散or連続、1変数or2変数、さらにそのそれぞれの試行の種類等に対応して複数存在します。)今後このシリーズで一つ一つ解説していきます。
これらを学んでいくことで、まだ抽象的に感じる確率関数などがしっかりと身についていきます。
確率変数/分布のまとめと関連記事
・確率質量関数でのXとxの違いに注意する。
・確率変数は離散型と連続型に分かれ、それによって以下のような違いがある。
・確率質量関数は離散型、確率密度関数が連続型。
・連続型確率分布では、1点での確率が0になる(1/∞:イメージ)ので、確率密度関数をある区間で積分することによって、指定した区間を取る確率が面積として求まる。
統計学シリーズ
第1回:「統計学入門;イントロダクション」
第2回:「(今ここです)確率分布の種類と意味」
第3回:「『ベルヌーイ分布・二項分布』と期待値E[X]、分散V[X]」
シリーズ一覧>>「統計学・データの分析まとめページ」<<
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集をコメント欄にて行なっています。
また、 いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

