
機械学習を0から学ぶシリーズ第1回(回帰の基礎と必要な数学)
はじめに。
機械学習を深く理解するためには、プログラミングの技術だけでなく、その背景となる数学を知る必要があります。
また、高校や大学で学んだ数学が様々な形で応用されていることを知ることは大変意義深く、ベクトル(線形代数)と偏微分(解析)、確率・統計といった(特に高校では)別々に教わったものが点と点で結びつく様子は感動的ですらあります。
しかし、逆にこれらの数学が苦手で避けてきた人や、学びの場から離れて久しい人にとっては『高校数学〜大学教養レベル』の数学をいきなり学び直すことは大変なことです。
そこで、このシリーズでは弊サイト『スマナビング!』に蓄積された、『高校生向けの様々な分野の基礎解説記事とリンク』させながら、機械学習に必要な数学を学んでいきます。
※このシリーズは『0から最小限の知識をわかりやすく』をモットーにしています。
厳密さや個々の深掘りよりも、まずは全体を俯瞰できる様になることを優先していることをご了承下さい。
目次(タップした所へ飛びます)
回帰分析とは何か
機械学習といっても様々な種類がありますが、まずはじめに学ぶものは『回帰(分析)』では無いでしょうか。
今回はその中でも最も単純な部類である、単回帰分析を学びます。
データの散らばりから将来を予測する(一次関数)
ではさっそく、回帰分析の中でも最も単純な“単回帰分析”の解説から始めます。
「単」と付いている理由は、予測するモデルが変数一つで表せるためです。
例えば、夏休み中の1日あたりの勉強時間と夏休み明けのテストの点数のデータを集めておいて、その傾向を式で表し、“今年の夏に●時間勉強したら、△点くらいは取れるだろう”といった予測を立てるものです。
実際には、1日あたりの勉強時間(変数一つ)で予測できるわけがなく、もっとあらゆるデータ(ex,勉強の効率や、元々の成績の良し悪しなど・・・)を集めて分析する必要があります。
この様に、一つの条件よりも沢山の条件(変数)を使って分析することを『重回帰分析』と言います。
適当に例を挙げたグラフにプロットしたものが以下の<図1>です。
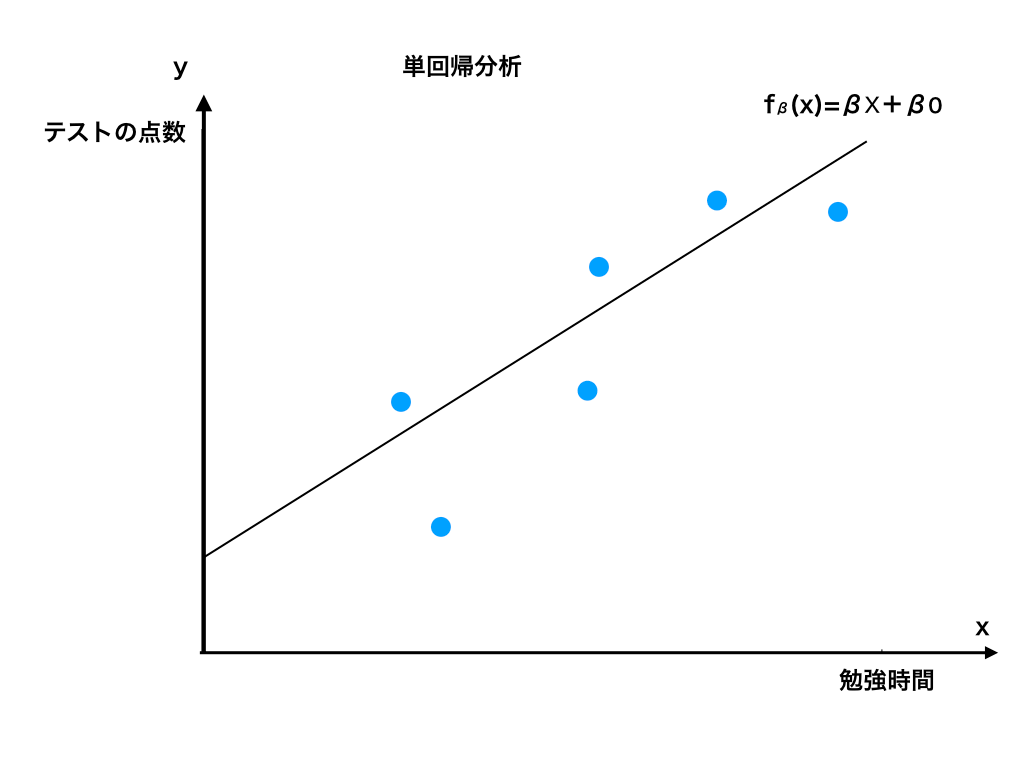
<図1:単回帰分析のイメージ>
このグラフを見ると“だいたい$$”h_{\beta}(x)=\beta x+\beta _{0}$$という一次関数で表せることがわかります。
(中学校や高校で学んだ、一次関数の\(y=ax+b\)の代わりに\(\betaと \beta_{0}\)をおいているだけです。)
普通関数はh(x)=の形で表す事が多いですが、hと(x)の間にβという文字(これをパラメータと呼びます)が挟まっていますね。
そして、右辺の係数と定数項がβで表されている事が確認できます。
これは、のちに行う『最適化』のためにおいています。
この関数のxに1日あたりの勉強時間を代入することによって$$y=h_{\beta}(x)$$、すなわちテストの点数が大体予測できる(はず)です。
予測したグラフとの「誤差」
さて、hβ(x)で表した関数のグラフと実際のデータの差を見ると、当然ぴったり同じになる訳ではなく誤差が<図2>のように存在します。
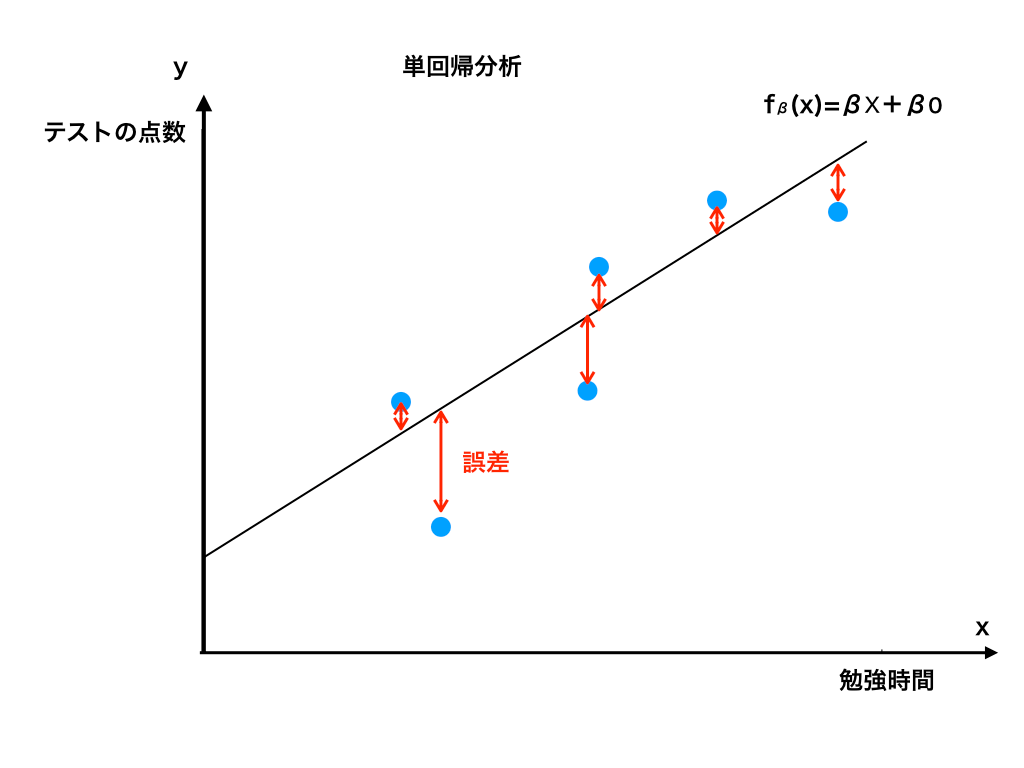
<図2:hβ(x)と誤差>
誤差を修正するための”目的関数”
ここで、誤差が予測したモデルと比べて大きいと意味がないですね。
なるべく誤差を小さくするために、機械(コンピュータ)がデータから学習してもらえれば、我々は大変楽になるのです。
そこで、予測した一次関数の係数と定数項の値(=一次関数の切片や傾き)を色々と変化させて、データとの誤差を小さくしていく必要があります。
そのために登場するのが”目的関数”と呼ばれる関数です。
目的関数の係数が”1/2である理由”と”2乗するワケ”(最小二乗法)
さて、目的関数は以下の式で表すことができます。
$$J(β)=\frac {1}{2}\sum ^{n}_{i=1}\{ y^{(i)} -h_{β} ( x^{(i)}) \} ^{2}$$
いきなり数式の羅列になって混乱している方もいるかと思いますが、それぞれの意味とさらに詳しい解説ページへのリンクを貼りますので、じっくり理解していきましょう。
まずΣ記号ですが、これは『記号の下のi=1から記号の上のn番目まですべて足し合わせる』という意味です。
(Σ記号については→「シグマ記号と数列の和をわかりやすく解説!」で紹介しています。)
そしてΣの右にある、yiはi番目のデータ、hβ(x)iは、予測した一次関数がi番目のところでいくつの値をとるか、ということを表しています。
つまりこれらをまとめると、”(『実際の値ー仮定した一次関数』=”ズレ”の値)の2乗”を、
n=1番目のデーター,2番目,,,n-1番目、n番目まで全て足し合わせて、
最後に1/2を掛けたものであると言えます。
2乗する意味と1/2倍するワケ
単純に、差を足し合わせるだけで良いのに、なぜわざわざ2乗するのか?という疑問については、ズレが”正の値“も”負の値“も取ることを考えると理解できます。
(参考:「分散と標準偏差を解説!」で詳しく紹介しています。)
今仮に、n=4、(目的関数ー仮説関数)が(-5),(3),(-2),(4)であったとします。
この時、単にズレを足し合わせると、(-5+3-2+4)=0、と実際には上下にズレているのに正負が打ち消しあって0になってしまいます。
これではどのくらい仮説から外れているかわかりません。
そこで、二乗したものを足し合わせることで、(25,+,9+,4+16)=57と”数値”として量ることができるのです。
・次にΣの前に1/2倍している理由について。
これは、次の項で解説する『勾配降下法』という”データのずれ”=誤差を小さくするための方法の途中で微分(偏微分)を行うのですが、Σの右側は上述した通り2乗していますから、{1/2(目的関数)2}'=2・1/2 (目的関数)=(目的関数)となってシンプルな形にするために置いたのです。
(微分の復習は→「微分・積分法の基礎の解説記事まとめ」で行えます。また、偏微分については次回詳しく扱います)
なお、ここでもごく初歩的な微分公式だけ紹介しておくと、
\(f(x)=x^{n} \)を微分すると、\(f'(x)=nx^{n-1} \)あるいは$$\frac{d}{dx} f(x)=nx^{n-1}$$となります。
最適化問題と勾配降下法(上)
では、目的関数を最小化する(=すなわち誤差を無くす)ための方法を学んでいきます。
これを最適化問題といい(そのままですね)、幾つもの方法があるのですが、今回は”勾配降下法”を扱います。
これは、仮定した関数fβ(x)のパラメーター(β、β0:一次関数の係数と定数項でした)の値を変化させることによって誤差をなくすため、
→目的関数をパラメーターβ、β0で偏微分し、
→その導関数(微分した後の関数を”導関数といいます”(参照:「微分係数と導関数の意味と違いとは?」)が0になるように(傾き=が0)パラメーターをどんどん更新していくというものです。
・・・そろそろ??が浮かんできた人が多いのではないでしょうか。
この先は数式がまた増えてくるので、一旦第1回はここまでにしておきます。
一気にいろいろな情報に触れたので、(特に数学が久しぶりの人は)休憩を入れて復習をしつつ、次回をお待ちください。
次回:偏微分のキソと勾配降下法(下)へ
・次回は、誤差を小さくする『勾配降下法』の続きと、
・そのために必要な『偏微分』、『合成関数の知識』などを高校数学の記事と再びリンクさせながら、解説を行なっていきます。
※続編と、数学知識編を作成しました。
第0回:「機械学習の理解に必要な数学まとめ」
第1回:「今ここです」
第2回:「勾配降下法の為の偏微分・合成関数の微分」
第3回:「勾配降下法(最急降下法)の仕組みと手順」
・次回までの間におススメの記事
→「微分積分のまとめ記事」+「線形代数の超入門記事まとめ」
最後までご覧いただきまして、誠に有難うございました。
「スマナビング!」では、読者の方々のご意見や、記事のリクエストなどをもとに改善、記事の追加を行なっています。
・リクエストやご質問・ご意見がございましたらコメント欄までお寄せください。
・いいね!やシェア、B!,Twitterのfollowなどをしていただけると励みになります。
・その他のお問い合わせ/ご依頼等のお仕事関係のご連絡はお問い合わせページよりお願い致します。

