領域の応用(二):線形計画法とその発展分野
<この記事の内容>:(不等式を満たす)領域を利用して、『最大値』や『最小値』を求める問題(線形計画法)の解き方から、関連する発展分野の紹介まで幅広く紹介・解説しました。
<前回の記事>:「領域第1回:【不等式で表される領域の調べ方と図示の方法】」
目次(タップした所へ飛びます)
不等式で表された領域と最大/最小
領域を利用する問題の中でも、頻出なものとして、『不等式で条件が表され』、『x+4y』のようなx、yで表された式の値を問われるものがあります。(これを『線形計画法』ということがあります。)
実際に以下の例題を通して、そういった問題の解法を解説していきます。
線形計画法:理解のための例題1
例題1:)
今、次のような3つの不等式
・y<-x+2
・y>2x+2
・y≧0 (すなわち、x軸の上側)
を全て満たすとき、
\(y-x の最大値と最小値を求めよ。\)
解き方の紹介と流れ
さっそく、この問題の解き方の流れを紹介していきます。
領域の図示
まずは、例題で与えられた3つの不等式によってできる領域を、「領域(1):不等式の図示の方法と調べ方」の考え方を用いて、xーy座標平面上に図示します。
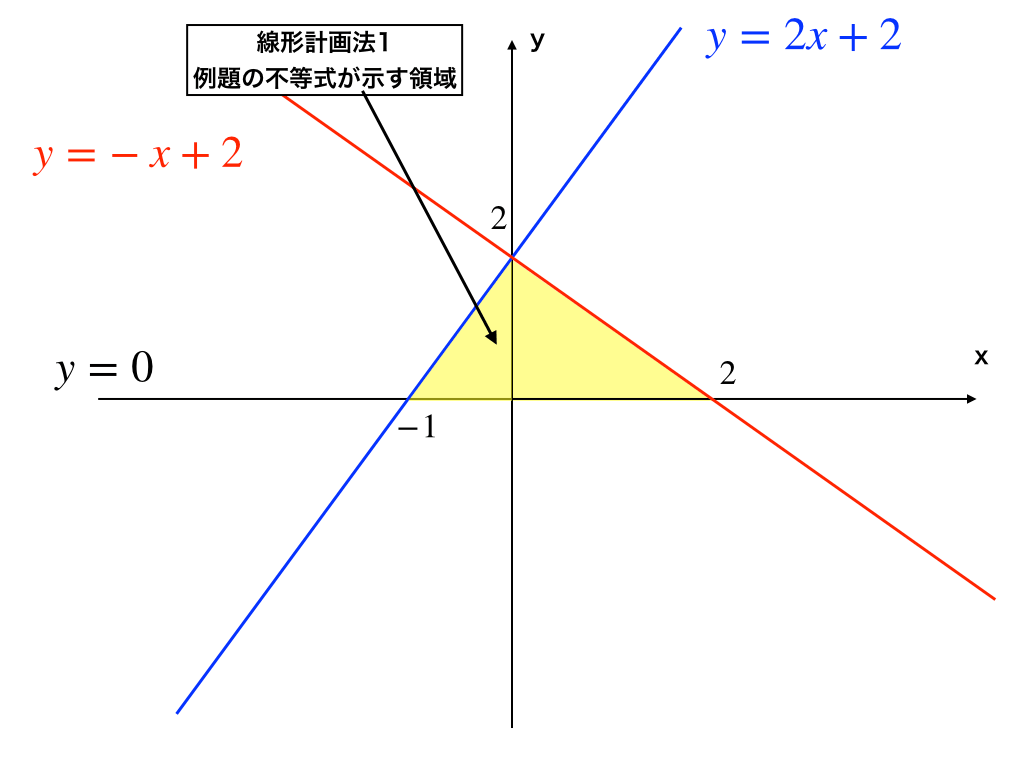
青色の直線がy=2x+2、赤色の〃がy=-x+2、そしてx軸をそれぞれ描き、不等号の向きに注意して領域を調べます。
その結果、イエローで塗られた部分が先ほどの”3つの不等式を満たす領域”(交点・境界を含む)です。
=k とy切片
ここで、【y-x の値】とは一体何を意味するのかを考えてみます。
【y-x】の値を問われているので、この未知の値を”k”と置くこととすると、$$y-x=kと式を立てることが出来$$
-xを移行すると、\(y=x+k\)となって、『k=求める最大・最小値=y軸の切片の値』が全て等しくなることがわかります。
つまり、この最大値・最小値の問題は”k”、すなわちy切片の値を求める問題に帰着させることができます。
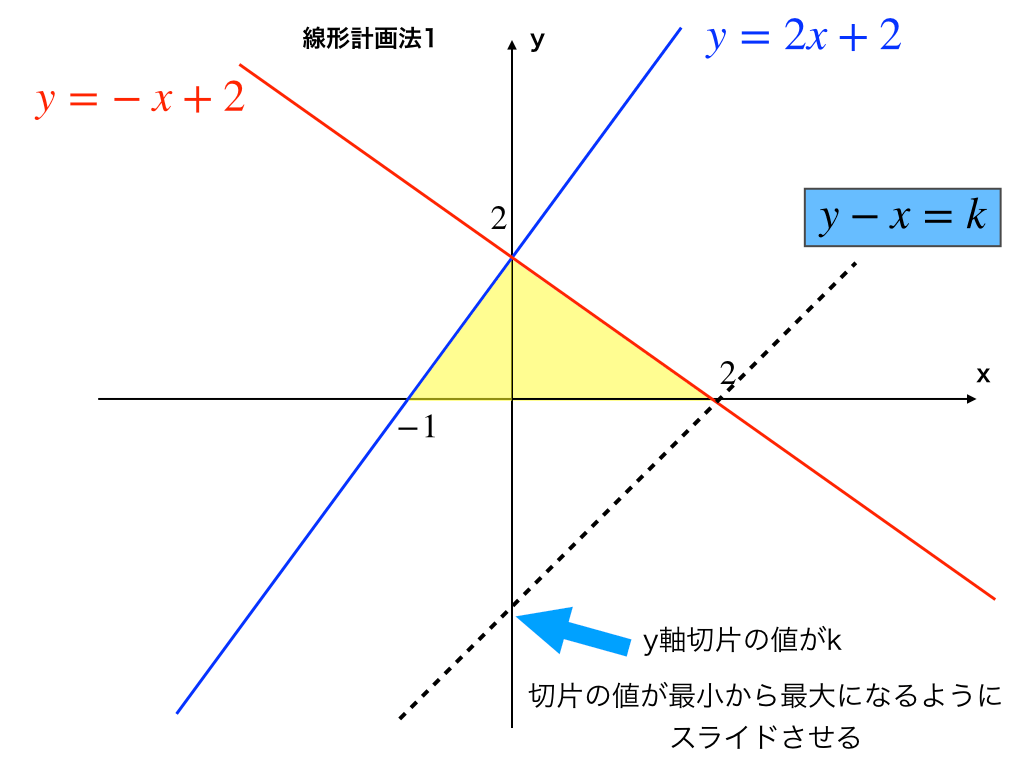
上下にスライドさせよう
切片の値が題意の最大・最小であることがわかったので、\(y-x=k \leftrightarrow y=x+k\)を上下に動かしてみます。
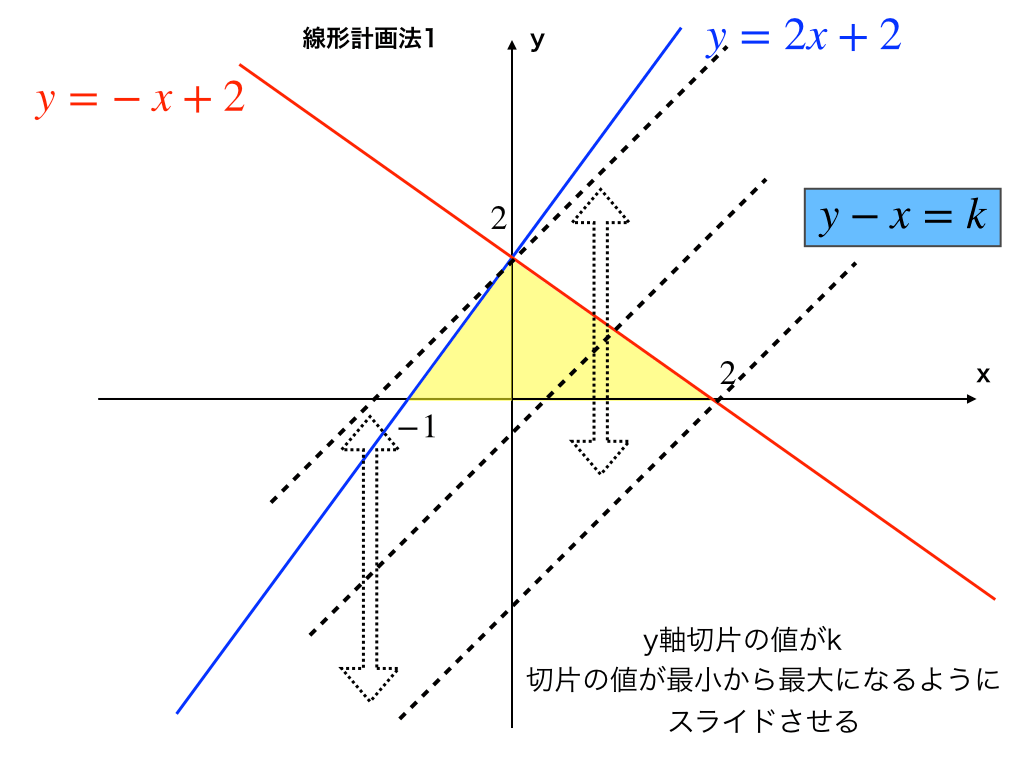
y切片の範囲
上のスライドの結果、
・"k=y切片"が最小になるときは、【x軸とy=-x+2の交点(2,0)を、y-x=kが通るとき】で、
・最大になる場合は、【y=2x+2とy=-x+2の交点(0,2)を、同様にy-x=kが通るとき】であることがわかります。
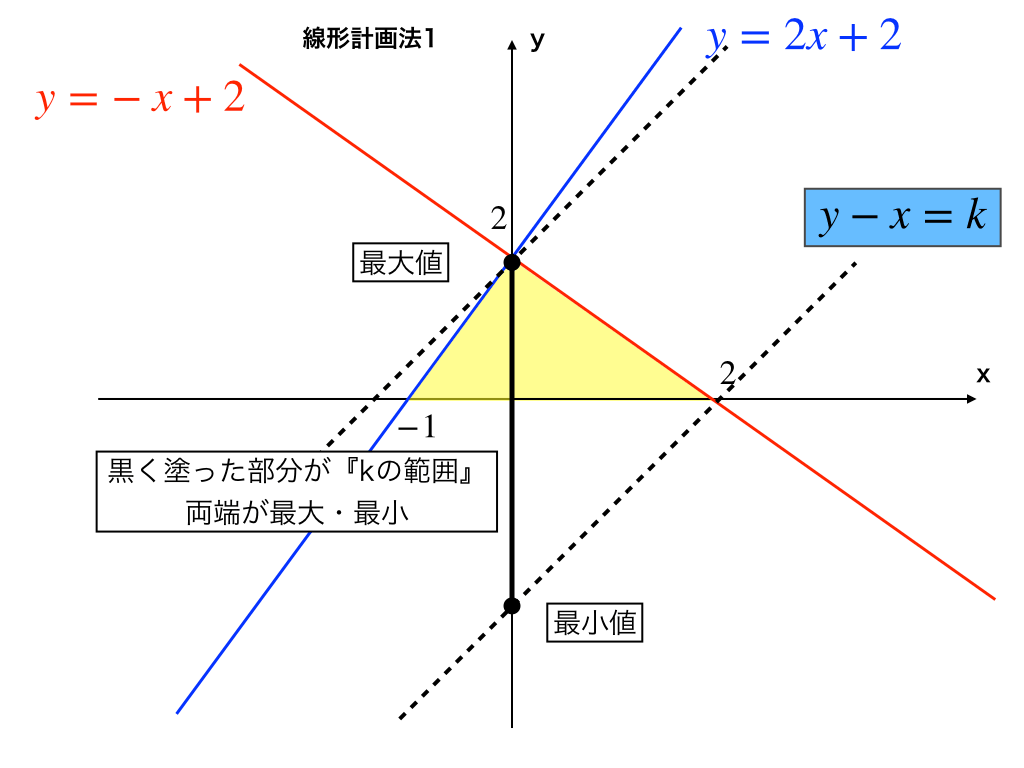
結局、上の図3のy軸上の黒丸から黒丸まで黒で塗りつぶした部分がkのとる値の範囲となり、
−2≦k≦2
ゆえに、y-xの最大値が2、最小値が−2
・・・(答)とすることが出来ます。
定着用問題(領域が曲線で囲まれている場合)
では、今度は領域が直線だけでなく「曲線」でも囲まれている場合を考えます。
要注意なポイントがあるので、しっかりと確認しておいてください。
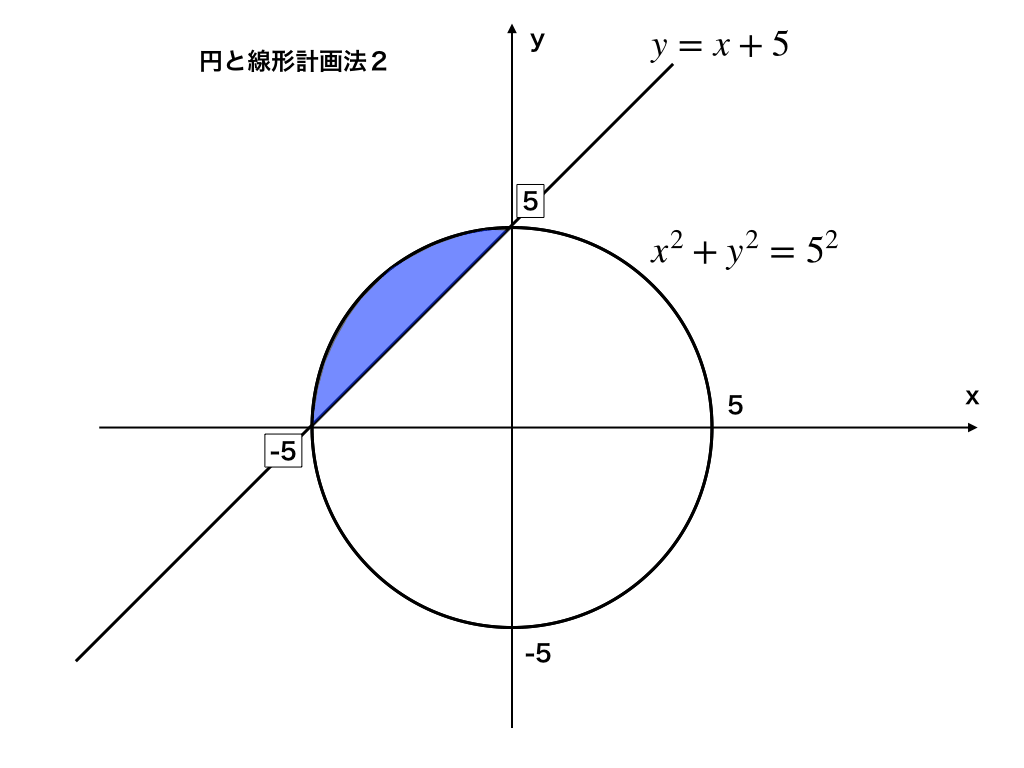
例題2:いま、\(y>x+5と、5^{2}>x^{2}+y^{2}\)の不等式を満たす、”5x-y”の最大・最小値を求めよ。
解答(線形計画法2)
これまでと同じく、領域を図示していきます。(青色に塗られた部分:境界と交点を含む)
=kの式をを描きスライドさせる
y-5x=kということは、傾きが”5”であるため、かなり急である事が想像できます。
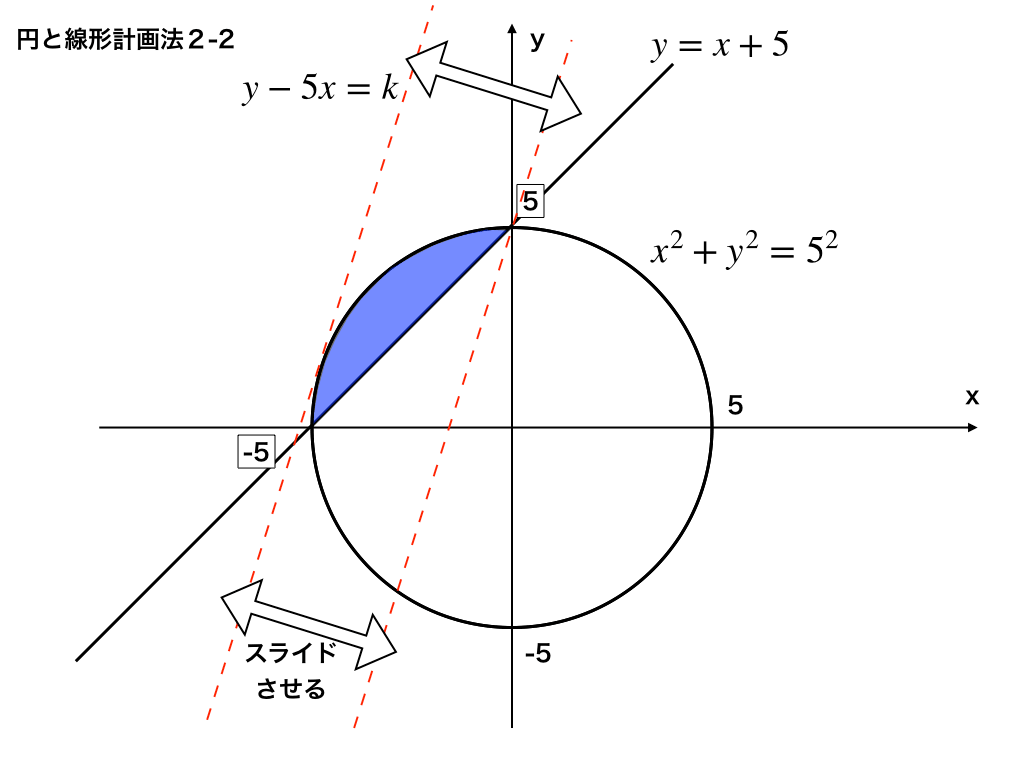
上の図のように、青色の部分を通過するように\(y=5x+k\)を移動させます。
【最重要ポイント】曲線の場合は交点ではなく接点に注目する!
この一連の解法でもっとも注意しなければいけないところがこの項です。
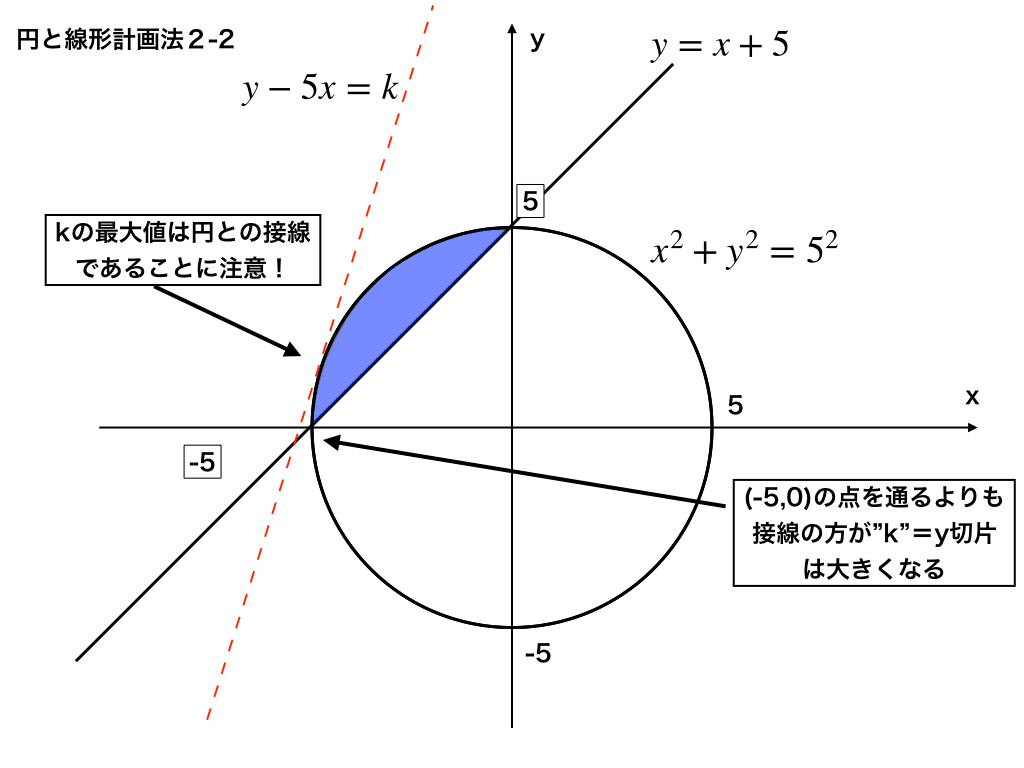
最小は、y軸上の(0,5)を通るときなのですが
最大値は、先ほどの例題1で求めたような交点を通るときではありません。
よく図を見ると、交点(-5,0)を通るときのy切片よりも、円\(x^{2}+y^{2}=5^{2}\)と\(y=5x+k\)が接している場合の方が値が大きいのです。
では、この接点を通るときの”k”を求める必要が出てきます。
円と接するときのk(点と直線の公式の利用)
円と接しているので、直線y-5x=kと円の中心点である(0,0)のキョリは半径と等しくなるはずです。
したがって、点と直線の距離公式:$$\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}$$より、
$$\frac{|5\cdot 0+1\cdot 0+k|}{\sqrt{5^{2}+1^{2}}}=5$$
これを解いて、\(k=\pm 5\sqrt{26} \)。図よりkは正なので、\(k=5\sqrt{26}\)
これらをまとめて、
kの範囲は、\(5≦k≦5\sqrt{26}\)
ゆえに、$$最大値;5\sqrt{26} 、最小値5・・・(答)$$
このやり方で、ほとんどの入試問題は解けます。
次の項は、発展分野(難関理系・医系志望の人用の”ニュートン法”と社会人の方向けの”勾配降下法”)の紹介です。
線形計画法と数理最適化【発展】
今回紹介した方法は、『数理最適化』という学問のうちの一つで、先述したように「線形計画法」と名付けられています。
関連する(数理)最適化法の例
今回は、最大・最小値を求める関数が一次でしたが、他の方法として2つほど最適化法の例を挙げておきます。(他にもたくさんの種類があります)
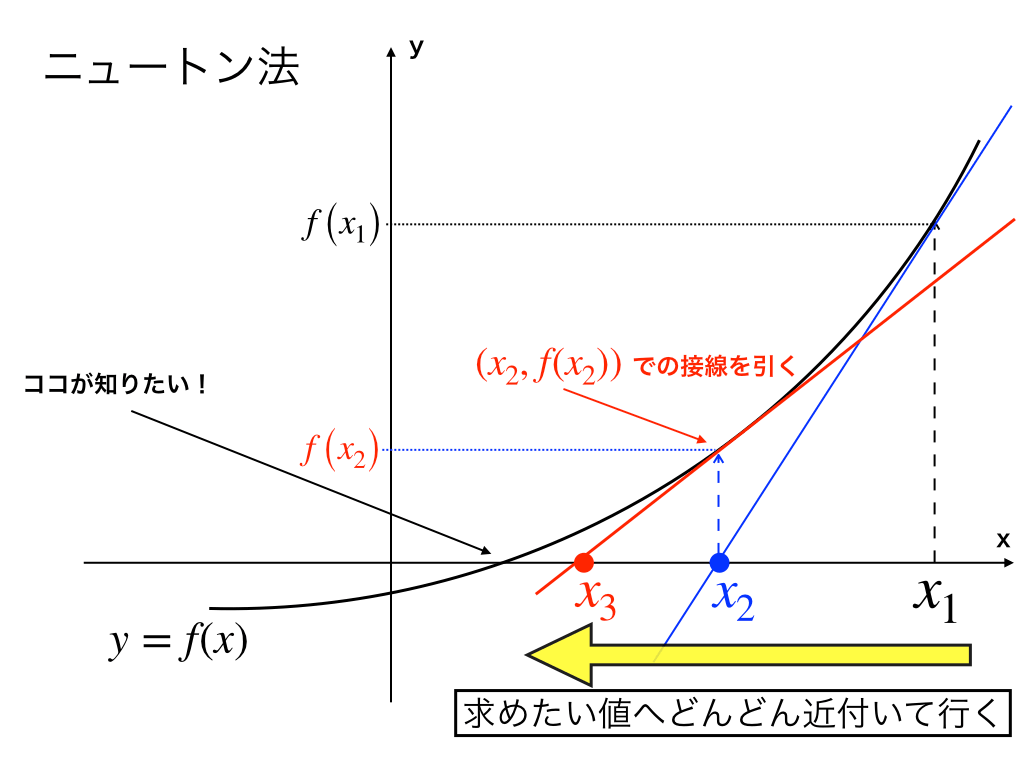
一つ目は『ニュートン法』です。
これは、高校数学3の知識で理解できるように解説記事を作っているので、難関理系・医系を目指す方は一度目を通しておいてください。
>>「数Ⅲ微分法の応用:ニュートン法の仕組みと問題の解き方」<<
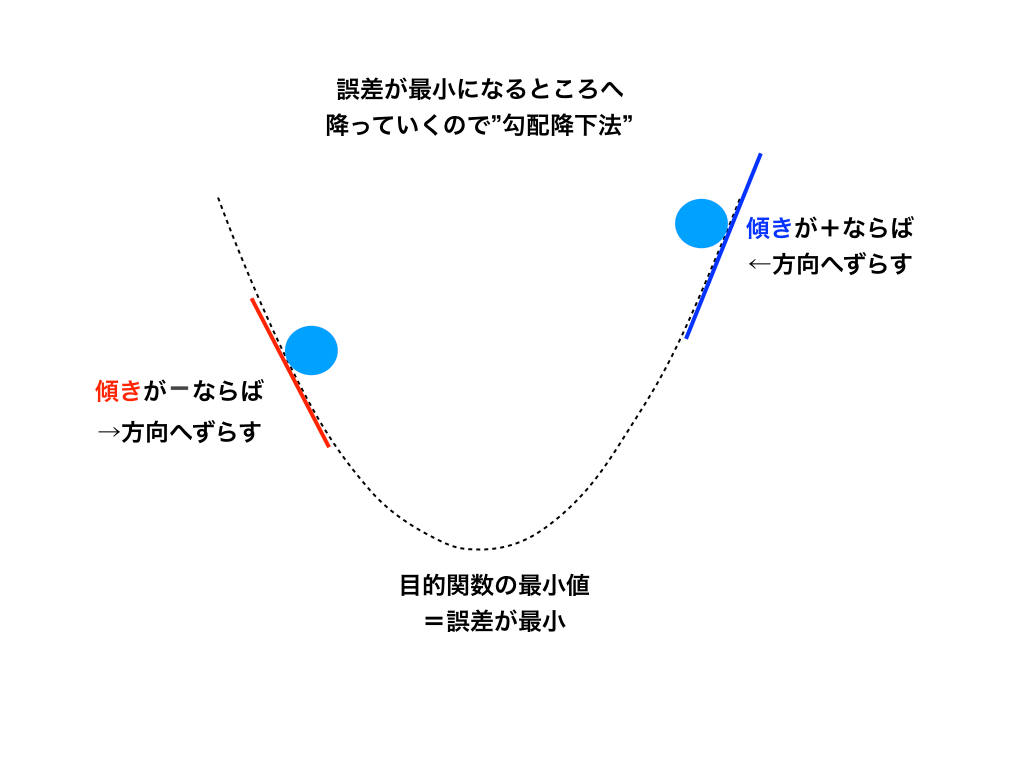
2つ目は『最急降下法(勾配降下法)』です。偏微分(大学教養レベル)が必要なので、興味のある方や機械学習を学んでいる方はご覧ください。
>>「最急(勾配)降下法の意味と仕組みをわかりやすく!」<<
参考1:「高校数学で0からはじめる【線形代数】まとめ」
参考2:「機械学習に必要な数学を一から学ぶ」
今回(線形計画法)の条件式を『等号』の場合に限定すると、→「ラグランジュの未定乗数法を解説」で紹介している方法で最大値(の候補)を求めることが可能です。(発展Lv)
まとめと図形と方程式の続編へ
今回は図形と方程式の「線形計画法」を紹介しました。
例題1・例題2くらいのレベルの問題であれば、大学の一般入試でも出題されることが多いので必ずマスターしておきましょう。
また、難関私大などではこの『線形計画法』をもっと具体的な問題(売り上げや生産高を最大にする問題など。)として出題してくる事があります。
そのような大学を志望している人は、過去問や類題を早めに解いておく事でアドバンテージを得る事が可能です。実際に、現実世界でも『計画』という名前がつく様に、工学や経営学など様々な分野で応用・活用されています。
領域シリーズ一覧
〜〜軌跡と領域〜〜
第一回:「領域の調べ方と図示のポイント」
第二回:「今ここです」
第三回:「軌跡の基本がわかる!例題を解きながら解説」
第四回:「(作成中)条件を満たす線分の通過領域」
〜〜図形と方程式のまとめページ〜〜
・その他のお問い合わせや、ご依頼に付きましては、サイト上部の【運営元について】のページよりご連絡下さい。

