
高校数学の知識から始める機械学習<第3回>
<今回の内容>勾配降下法(最急降下法)の具体的な手順とイメージまとめ
第1回「回帰分析とは?その意味と勾配降下法(上)」、
第2回「勾配降下法のための偏微分・合成関数の解説」
に引き続き、目的関数を最小化する『勾配(最急)降下法』の手順や、
その理論を理解するために必要な数学を紹介していきます。
目次(タップした所へ飛びます)
単回帰分析(1)の復習
第1回では、『夏休み中の勉強時間』と『その後のテストの点数』の関係という、1変数での予測方法として、一次関数を使用してモデル化する(これを『単』回帰分析と呼びました)ことを学習しました。
目的関数の復習と勾配降下法へ
加えて、その際に実際のデータとの誤差を”目的関数”を使って計算することを学びました。
<目的関数の式>
$$J(β)=\frac {1}{2}\sum ^{n}_{i=1}\{ y^{(i)} -h_{β} ( x^{(i)}) \} ^{2}$$
この式の意味は、『実際のデータと一次関数"hβ(x)=βx+β0"で仮定した値の誤差を二乗し*、その2乗をi=1番目のデータからi=n番目のデータまで足し合わせたものに1/2をかけた』ということでした。
*)2乗の理由:誤差がプラスのデータとマイナスのデータを足し合わせた時、数値が相殺されることを防ぐため。
最急降下法(下)のわかりやすい仕組み
さらに前回、『「第2回:勾配降下法を理解するための「偏微分」・「合成関数の微分」』を紹介したので、この項では実際にどのようにして目的関数を最小化していくのか、そのメインの部分を解説することにします。
パラメータを次々と更新させる事で目的関数を0に近づける
では、目的関数を最小化する、言い換えれば仮定した一次関数hβ(x)をデータに近づけるにはどうすれば良いのでしょうか。もう一度hβ(x)とデータのグラフを見てみましょう。
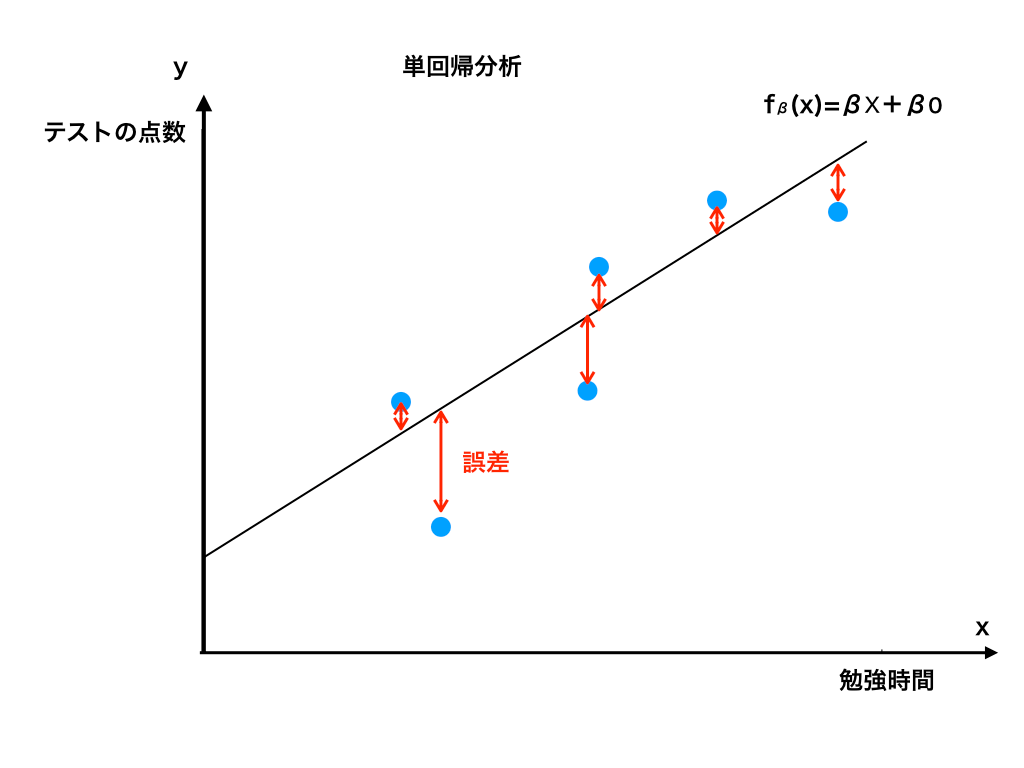
ここで、パラメータ(=傾きβと切片β0)を上手く変えてあげることができれば、よりデータにfitした一次関数になることがわかります。
目的関数をパラメーターβ,β0で偏微分していく
シグマの性質(→「Σ公式と数列の和の解説」)でも紹介していますが、微分の順序はd/dx Σ ◯ でも、Σd/dx ◯ でも同じ結果になります。
$$J(β)=\frac {1}{2}\sum ^{n}_{i=1}\{ y^{(i)} -h_{β} ( x^{(i)}) \} ^{2}$$
ここからが本題です。
上の式で表される目的関数が0になることを目指すという事は、目的関数をβ、β0で偏微分した際に求まる”偏導関数”の傾きが正の時は0に近づくように、また、偏導関数が負の時も同様に0に近づくようにすれば良いのです。
ここが一番理解しづらいところかもしれません。
普通の二次関数のグラフと傾きを考えてみてください。<勾配降下法のイメージ図参照>
二次関数が目的関数で、その関数の上にある値を一番低い場所へ持っていく(=勾配を降らせる)には、その場所の接線の傾きと逆方向へずらしていけば良い→導関数をマイナス倍するというイメージです。
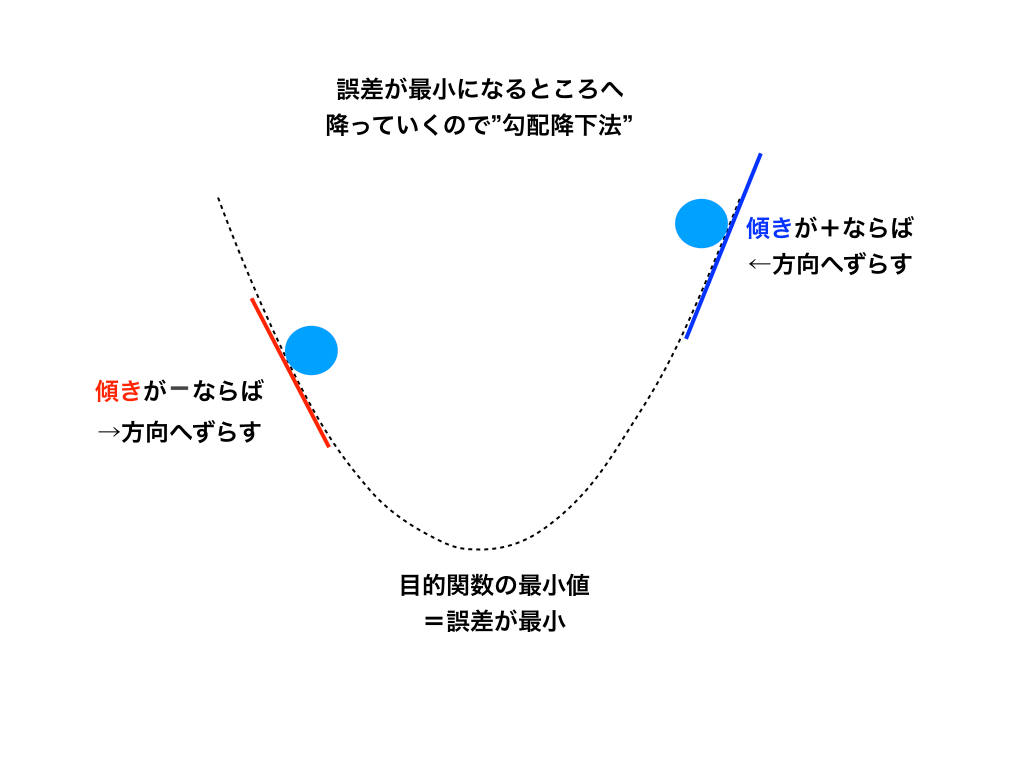
<勾配降下法のイメージ図>
勾配を降らせる方法と更新式
上の項で述べたとおり、”勾配を降らせる”から勾配降下法なのですが、具体的にはパラメータを次々と最適な新しい値に更新していく事によって目的関数を0に近づけていきます。
その為の”更新式”はβ、β0で以下のように示されます。
$$β_{新}=β_{前}ーη\frac{∂J(β)}{∂β}$$
$$β_{0}新=β_{0}前ーη\frac{∂J(β)}{∂β}$$
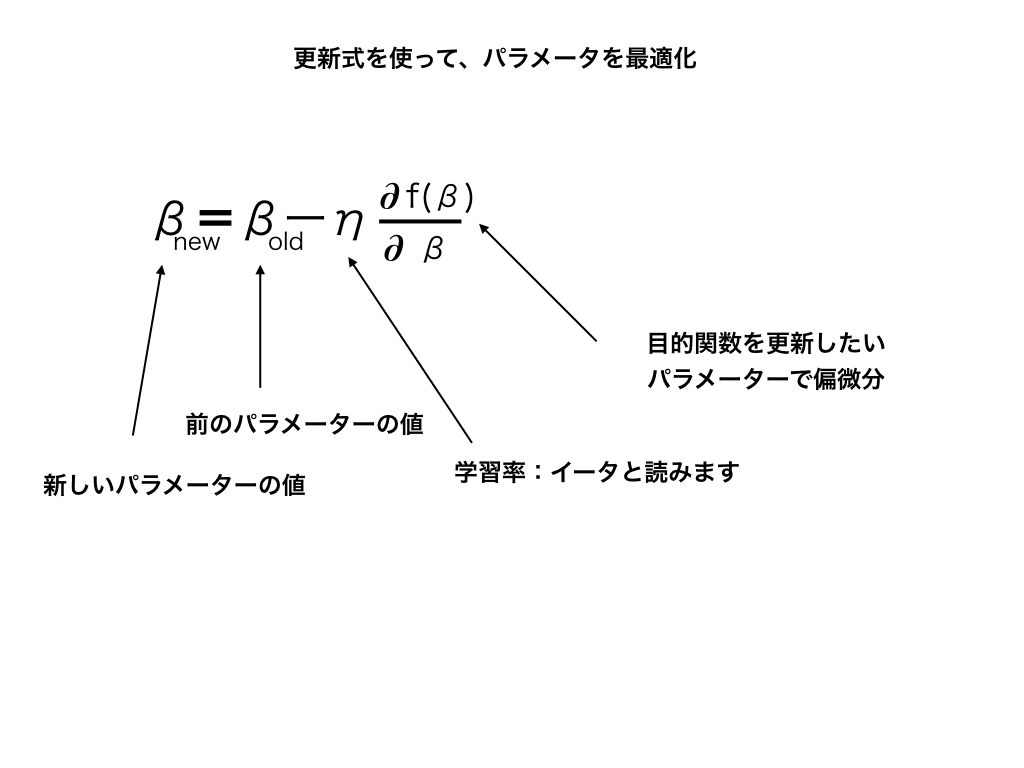
<パラメーターの更新式>
上の式の通りに計算を進める事で、誤差が最も少ない一次関数hβ(x)を見つけることができます。
学習率ηとは
$$β_{新}=:β_{前}ーη\frac{∂J(β)}{∂β}$$
の式で偏微分の前に付いている、見慣れない記号”η“の意味について簡単に紹介しておきます。
イータと読むこの文字は、“学習率”を意味します。
一般に、この値を1より小さく設定すると徐々にズレが修正される方向に収束していきます。
逆に1より大きい値を設定してしまうと、収束せず発散してしまいます。
この学習率ηの値をいくつにするのかが難しいところ(小さすぎると収束が遅くなる)で、ηの値を決めるだけでも様々な方法が考案されています。
勾配降下法の弱点
この様に、偏微分を利用する勾配降下法ですが、弱点もあります。その一つである「局所解」につかまるという事を紹介します。
三次関数などの極大値・極小値を持つ関数のグラフを思い出してみてもらえるとわかりやすいのですが、全体の最小値ではないにもかかわらず、平坦な場所があります。
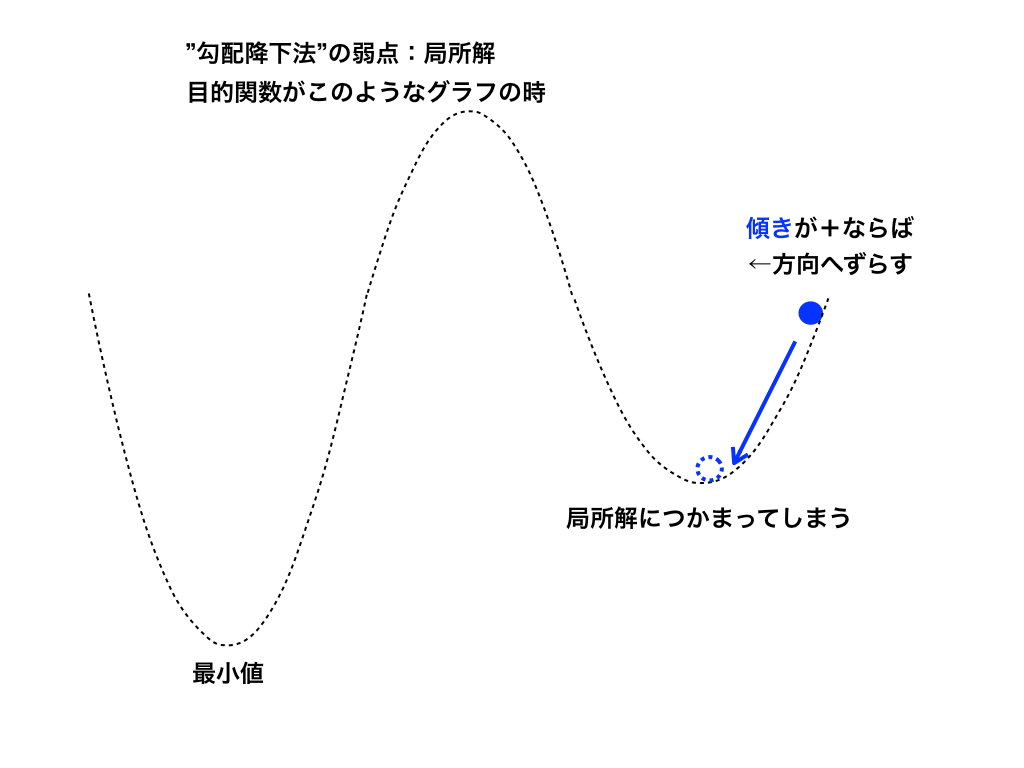
(機械学習では<図3>の様な場所を局所解と言います)
勾配降下法を用いて、目的関数の最小化を繰り返しているとこの局所解に入ってしまい本当の最小値にたどり着けない事があります。
加えて、勾配降下法(最急降下法)は、次回説明する重回帰分析でも学びますが、変数が増えるにつれて計算量が膨れ上がるという弱点もあります。
そこで考案された方法に、確率的勾配降下法やミニバッチ法があります。
そのそれぞれについて、次回の重回帰分析の以降で紹介していきます。
次回:重回帰分析へ
・(仮定した)モデル化した関数と実際のデータとの誤差を最小にする方法の一つが『最急(勾配)降下法』である。
・最急降下法では、仮定した関数のパラメーターを『更新式』を使って繰り返し計算することで最適化する。
高校数学ではじめる機械学習シリーズ
第0回:「機械学習のための数学知識一覧」
第1回:「機械学習(1)単回帰分析から始めよう!」
第2回:「勾配降下法のための偏微分・合成関数微分の解説」
第3回:「今ここです」
第4回:「(作成中):重回帰分析とその周辺」
今回も最後までご覧いただきまして、有難うございました。
記事のリクエストや、ご質問・ご意見を募集しておりますので、ございましたらぜひコメント欄にお寄せください。
・その他のお問い合わせ/お仕事等のご依頼に付きましては、お問い合わせページからお願い致します。

