力学が苦手な人へ!0から応用レベルまで詳しい解説記事まとめページ

力学(高校物理/基礎)まとめ【更新中】

＜この記事の内容＞：高校範囲の力学と、その理解に必要な数学などの解説記事をまとめています。

力学はそれ自体もかならず出題される分野ですが、他分野を勉強する上でも決してはずせない（例：単振動の理解がおろそかだと、波の式（波動）や電気振動（電磁気）が理解できない等,,,）最重要単元です。

物理選択の人はこのページの内容が『しっかりと』頭に入っているか、もしそうでなければ、ぜひ『他の人に説明できるレベル』まで何度も繰り返し読みこんでみて下さい。

そのレベルに達したとき、劇的に物理の理解度・成績が向上しているはずです！

【随時更新・記事の追加をしています。ブックマーク！推奨】

↓目次をタップ(クリック)するとその記事へ飛びます↓

等加速度運動（運動のキソ)

まずは基礎中の基礎である、「等加速度運動」と「投げ上げ・相対運動」などを見ていきます。

\(\begin{aligned}x=v_{0}t+\frac{1}{2}at^{2}\\v= v_{0}+at\\v^{2}-v_{0}^{2}=2ax\end{aligned}\)

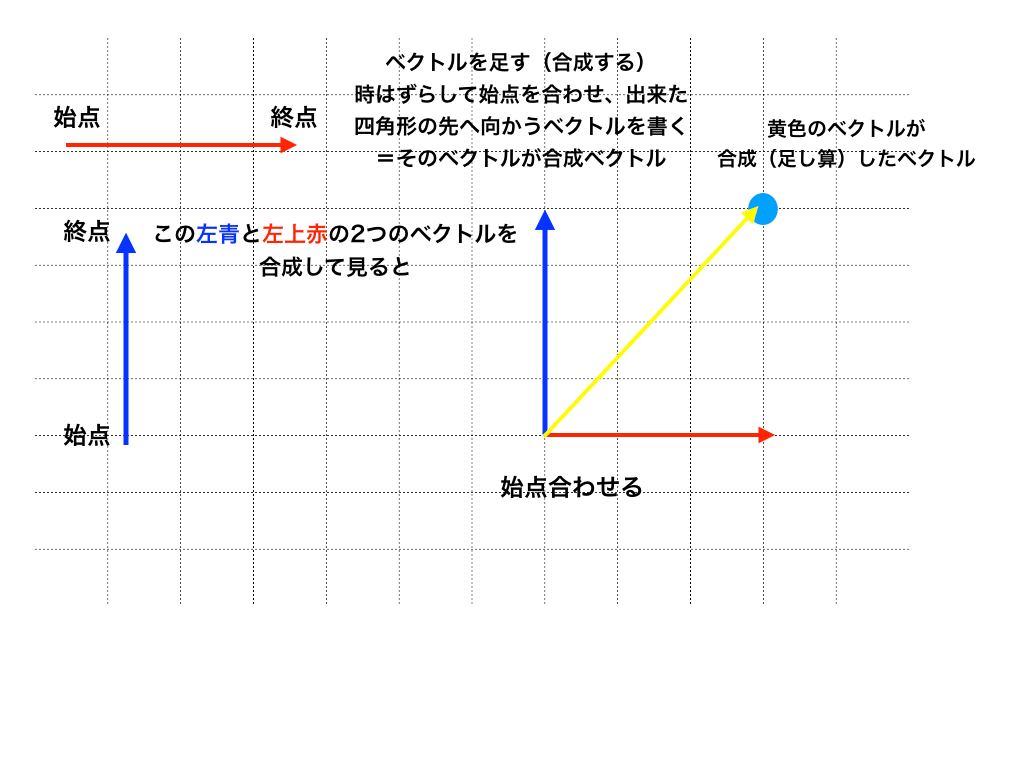
諸公式と数学的な準備

物理基礎の初めから「三角比」や「ベクトル」が必要な場面が登場します。

しかし

・学校のカリキュラムによっては、これらの数学を未修のまま先に物理に入ってしまう場合がある

・そもそも独学で勉強をしている

といった基礎的な数学で困っている方のために、「物理基礎(力学)必要な数学」を作成しました。

投げ上げ運動

「鉛直投げ上げ運動と“最高点を一瞬で求める”公式」

下向きに重力加速度gがかかっている状況で、

・真上に物体を投げ上げた際の運動の様子や、

・知っておくと非常に便利な公式

を等加速度運動の式を用いながら解説しています。

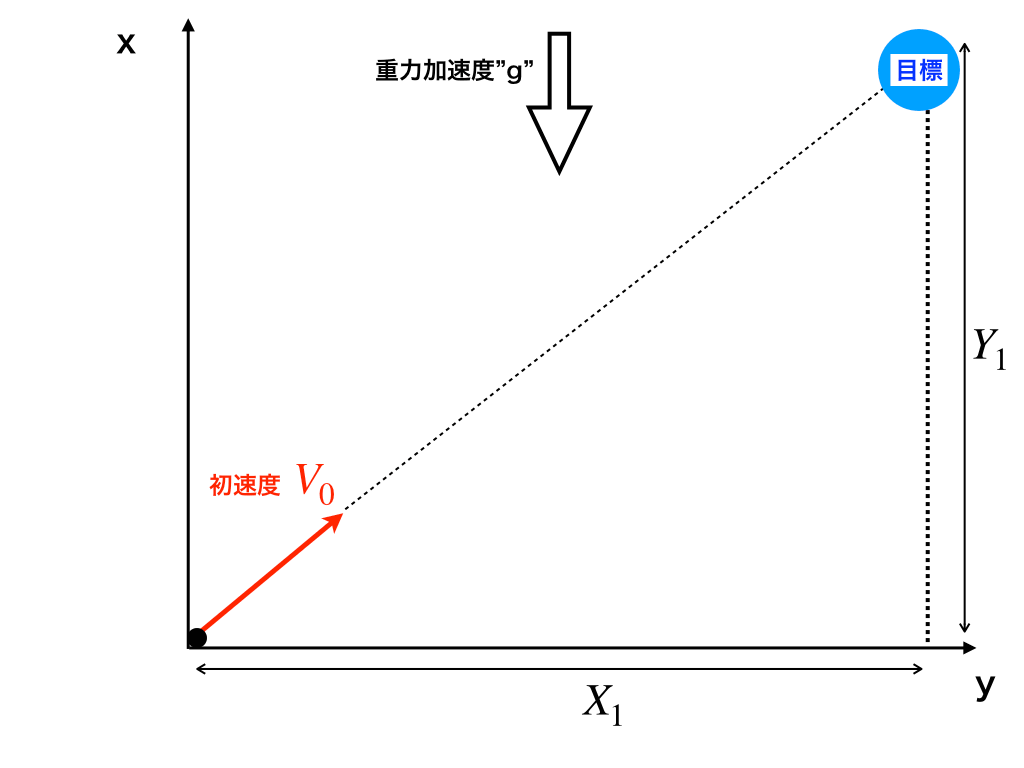
斜方投射

「斜方投射と軌道の式の導き方」

投げ上げの応用バージョンです。

この記事では、（真上ではなく）斜め上方向へ物体を打ち上げた時の運動の様子や、その軌道の式(上に凸の二次関数)を導く方法を紹介しています。

相対運動とモンキーハンティング

「”モンキーハンティング”の有名問題と相対運動」を通して、『相対運動』や二次元（縦×横）での等加速度運動を解説しました。

＜”モンキーハンティング”の問題図＞

運動方程式【最重要公式】

ma＝Fという、ニュートン力学において最も大切な運動方程式を中心に、

・方程式の立て方、

・力の釣り合い〜「二つの保存則」まで解説していきます。

力のモーメント・つりあい

「力のモーメントとは？」質点（大きさを０とする）の運動では考慮しなかった、剛体（大きさあり）の運動（回転運動＋並進運動）の解説を行なっています。

加えて【力のモーメント】や、有名問題である

・剛体が倒れない条件、

・さらに摩擦力との融合など、

イラストで力を図示しながら説明しました。

摩擦力の種類

よく混同しがちで、かつ頻出の「摩擦力”3”種類の違いと公式+例題の解法」を徹底解説しています。

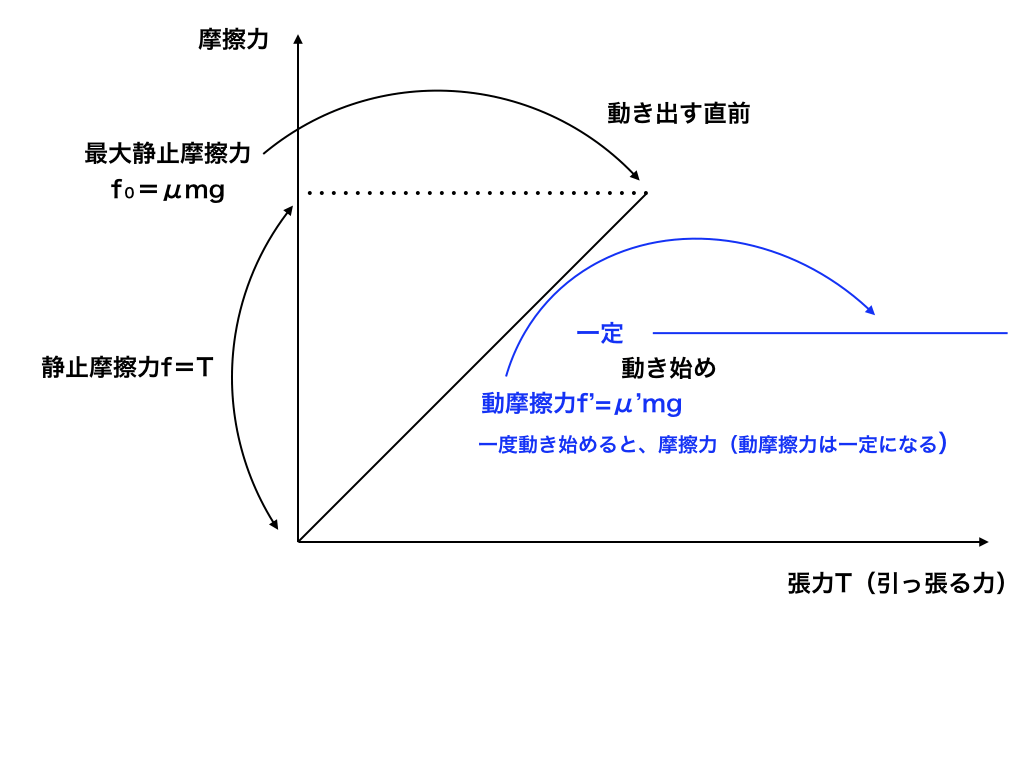
(上のモーメントの記事とあわせてご覧下さい！)

力学的エネルギーの種類と保存則(応用)

下で紹介している、運動量保存則とともに「ma＝Fから力学的エネルギー保存則を導出」する方法を解説しました。

$$\frac{1}{2}mv^{2}+mgh+\frac{1}{2}kx^{2}=Const.$$

運動量と力積・運動量保存則

「運動量と力積の関係〜はねかえり係数まで解説！」

ビジュアルで理解しやすいように、イラストを使いながら”力積”と”運動量”、そしてその保存則の基本を解説しました。

束縛条件と滑車/台上の物体の運動

「束縛条件とは？滑車と2物体の運動の問題で解説」では、

・運動方程式やつりあいの式の本数

と

・未知数の数が合わない（方程式の数が足りない）時に利用する、

『束縛(拘束)条件』を具体例を挙げながら図解しています。

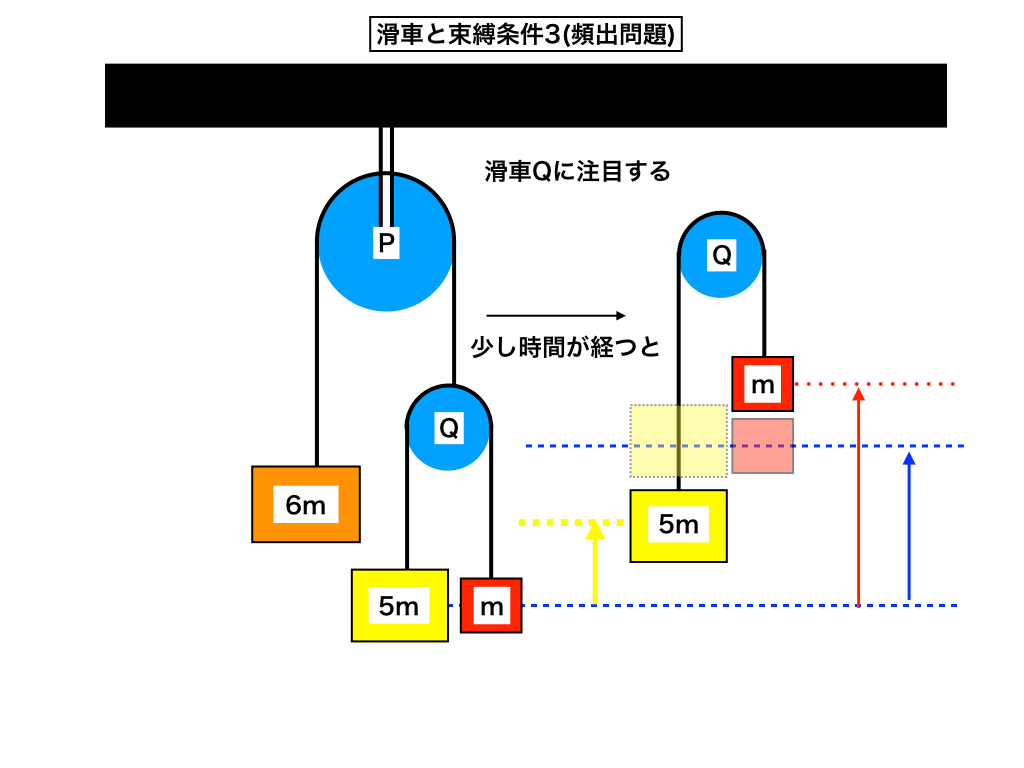
【参考：三物体と二つの滑車】

円運動と単振動・万有引力

ここからは、高校の力学のみならず高校物理全体としても最重要、かつ、電磁気の交流などでも必要となる考え方が詰まった円運動・単振動（＋万有引力の法則、ケプラーの法則）について扱います。

円運動と遠心力

等速円運動

「円運動と遠心力：ジェットコースターの問題」

エネルギー保存則や様々な力の釣り合いの式を用いて『ジェットコースターが落下しない条件』を求めます。

単振動

「単振動とは？0から応用問題まで解説」では、超重要分野である単振動の基礎的な公式を

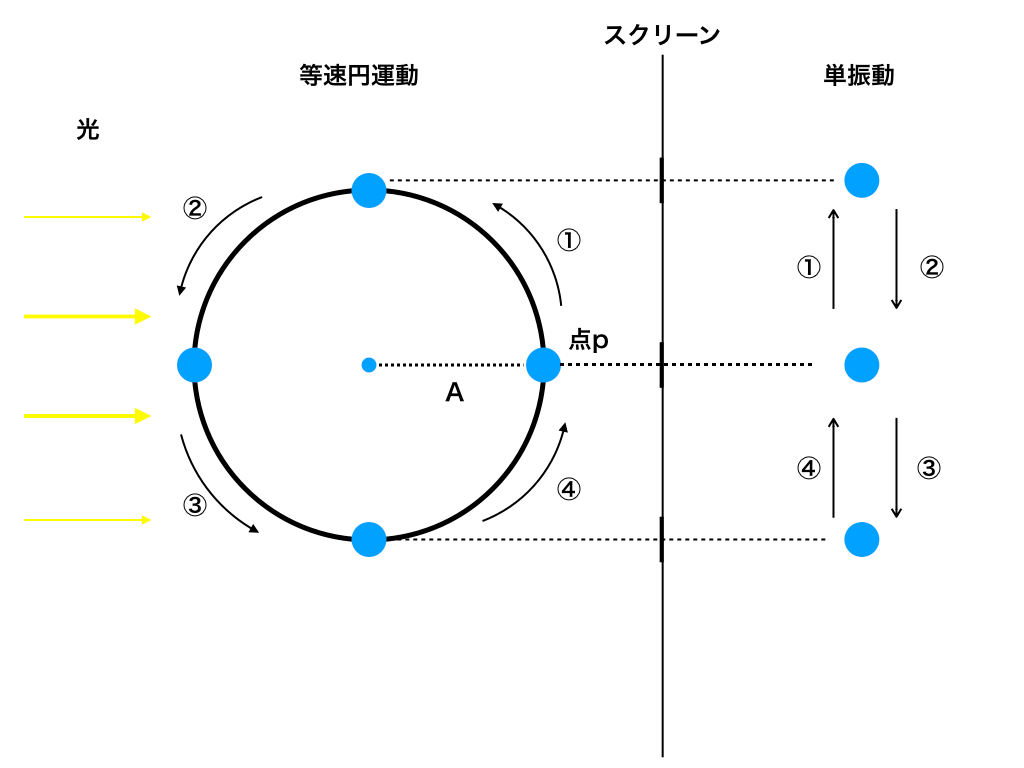
・「等速円運動」の正射影を使った方法と

・「微分」を使った方法の2種類で導出・解説しています。

(※：使用する数学Ⅲ程度の微分の知識は、『微分積分の解説記事まとめページ』にて紹介しています。)

\(\begin{aligned}x=A\sin (\omega t)\\v＝A\omega\cos (\omega t)\\a=-A\omega ^{2}\sin (\omega t)\\a=-\omega ^{2}x\end{aligned}\)

摩擦との融合

「摩擦がある単振動の問題」で、単振動する物体が非保存力である『摩擦力』によって徐々に振幅が狭くなって行く様子と、その現象を扱った問題を解説しています。

(※：「減衰振動のグラフ」\(y＝e^{-x}\sin x\)ではその数学的な問題を扱っています。」

浮力との融合

「浮力と《浮力を復元力とした》単振動」では、『そもそも浮力とは？』と言うところから、その応用問題までイラスト付きで解説しました。

単振り子と近似

「単振り子の仕組みと公式・近似」では＜下図＞のように、

【振り子のひもの長さに対して、振れ幅が非常に小さい時】に用いる『単振り子』の考え方と、ハイレベルな物理では必須の【近似】について紹介しています。

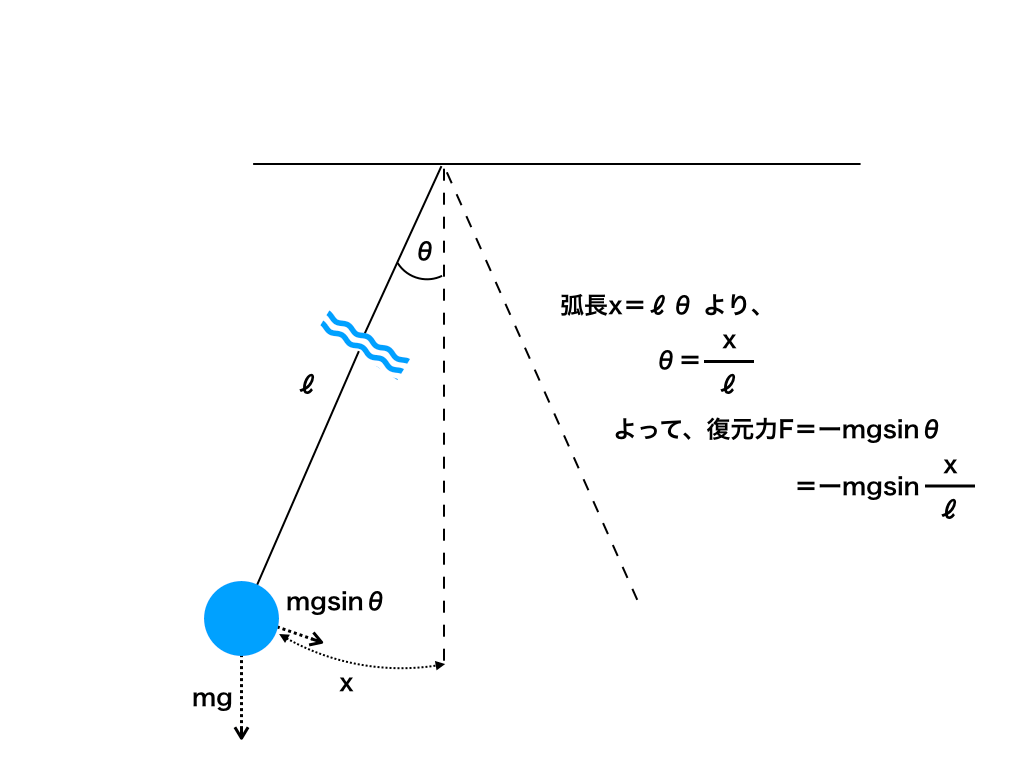
＜単振り子と近似＞

万有引力の法則

ここからは、重力加速度"g"が使えない様な『宇宙スケール』の力学・物体の運動を見ていきます。

万有引力の法則の基本公式は「第一宇宙速度と万有引力」で、続いて

$$F＝G\frac {mM}{r^{2}}$$

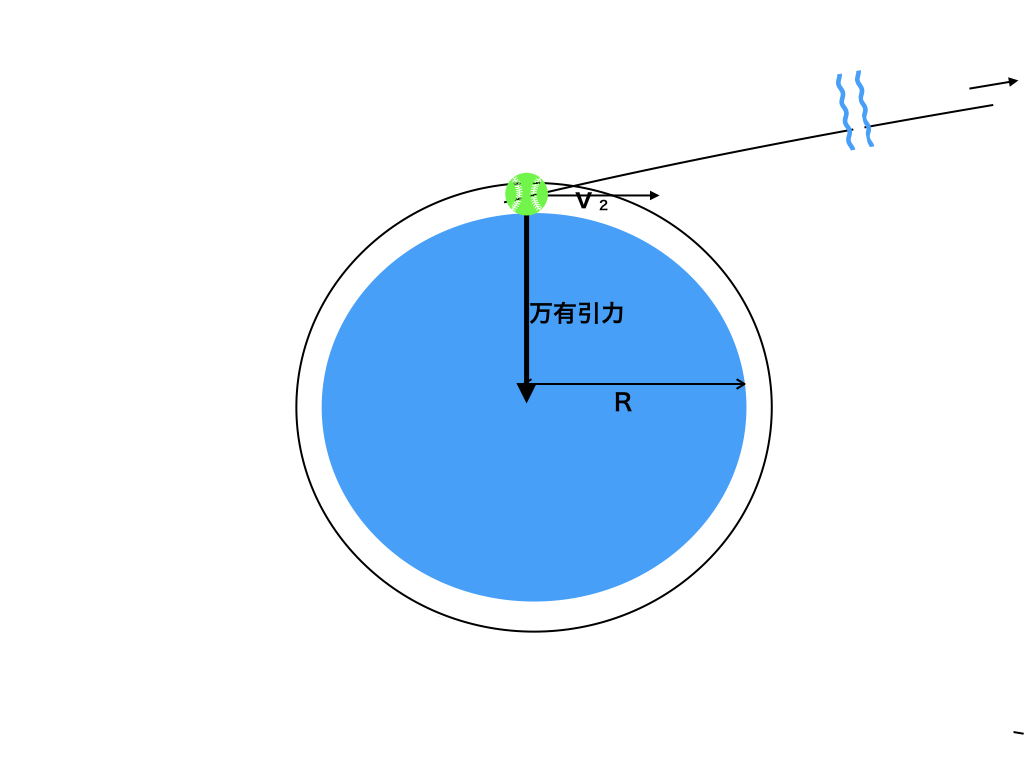
その”位置エネルギー”との関連は「第二宇宙速度と『万有引力による”位置エネルギー”が”負”』である理由」

で解説し【地球を脱出する速度：第二宇宙速度】の計算の仕方も扱いました。

ケプラーの３法則

「ケプラーの第一/第二/第三法則を分かりやすく」では、

・楕円軌道(第一法則)、

・面積速度(角速度)一定の法則(第二法則)、

・公転周期と恒星との距離が一定(第三法則)

などの証明・解説を行います。

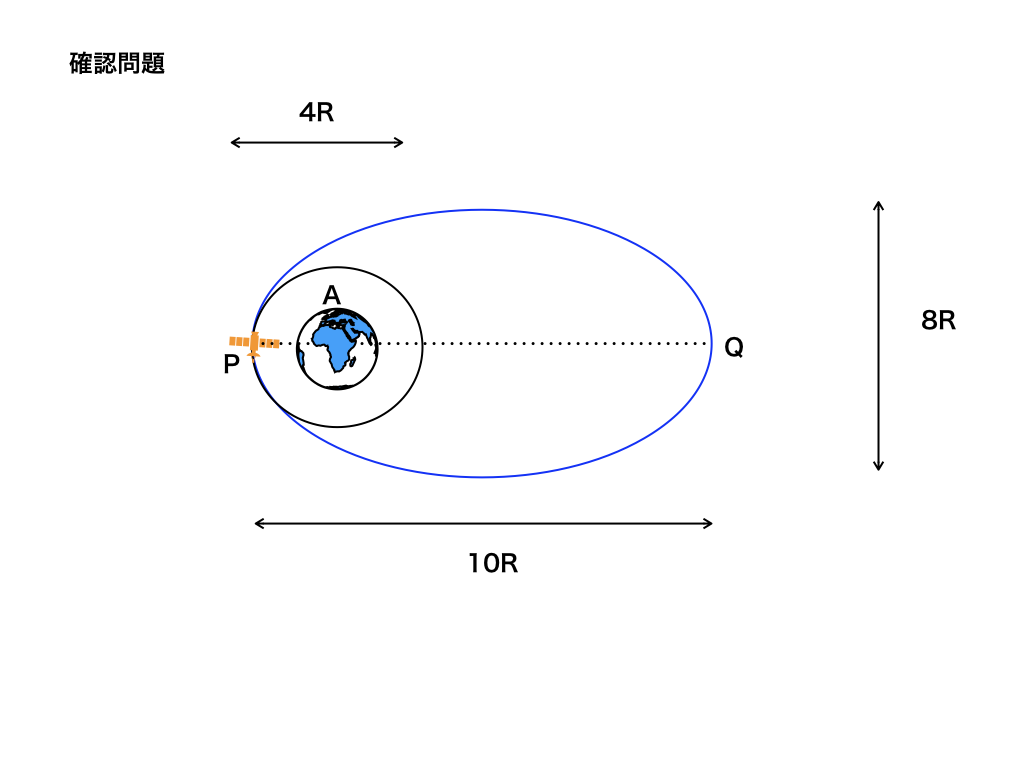
(※：数学で学ぶ楕円については、「数学Ⅲ:円錐曲線(3)楕円の方程式と性質」を参照してください！)

・・・(随時記事追加中。)・・・

力学まとめと関連分野

はじめに書いたように、力学は物理において全ての基礎となる分野であると同時に、他の”熱力学”・”波動”・”電磁気”・”原子物理”のすべての分野との融合問題も頻出です。

その為、どれだけ力学をしっかりとマスター出来るかが合否を分けます。

きっちりと公式を導き→覚えて、問題を多く解きましょう。

↓の様な交流回路や、「電気振動（LC回路）」でもこの記事の後半の知識は役立ちます。↓

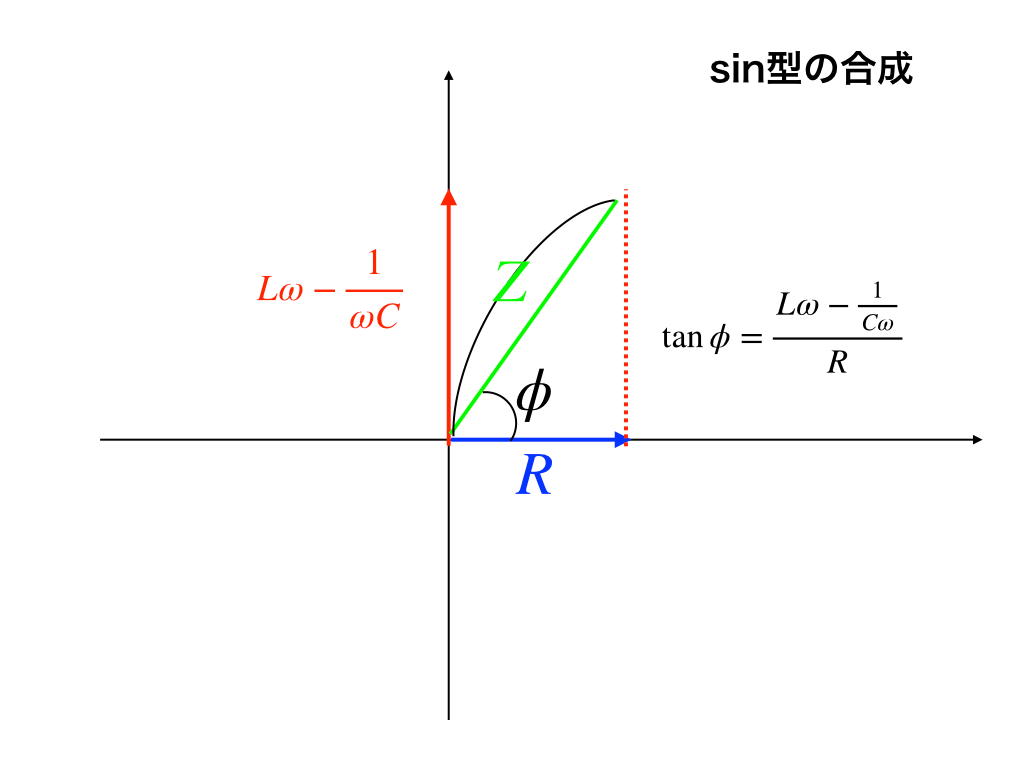
力学の次は、↓電磁気編をぜひご覧ください！

物理一覧と関連する記事へ

「電磁気分野の解説記事まとめ」

＞＞高校物理の記事一覧へ

【おススメ】演習用の問題集【5選】

「物理・物理基礎の演習用問題集5選」で、おススメの参考書・問題集とそのレベル・使い方などを紹介しています。

今回も最後までご覧いただき、有難うございました。

・「スマナビング！」への「お問い合わせや、ご依頼、タイアップ等のご相談」に付きましては、【運営元ページ】からご連絡をお待ちしております。