
単振り子(単振動第三回)
この記事では、単振動の第三回として、「単振り子」の運動と公式の導き方を解説していきます。
また、単振り子で頻出である「慣性力との融合問題」を記事の最後に確認用問題として掲載しました。
続編として、「浮力と単振動の融合問題」の記事を作成しました。
(まとめと関連記事よりご覧ください。)
単振り子と単振動
以前の単振動の記事を読んでいない方(or単振動が苦手な人)は、
先に右の記事を読んでからご覧ください。→「これでわかる!一から始める単振動」
単振り子とは、ゆるまない糸や棒の端に大きさを無視できるおもりを付けて吊るしたものです。
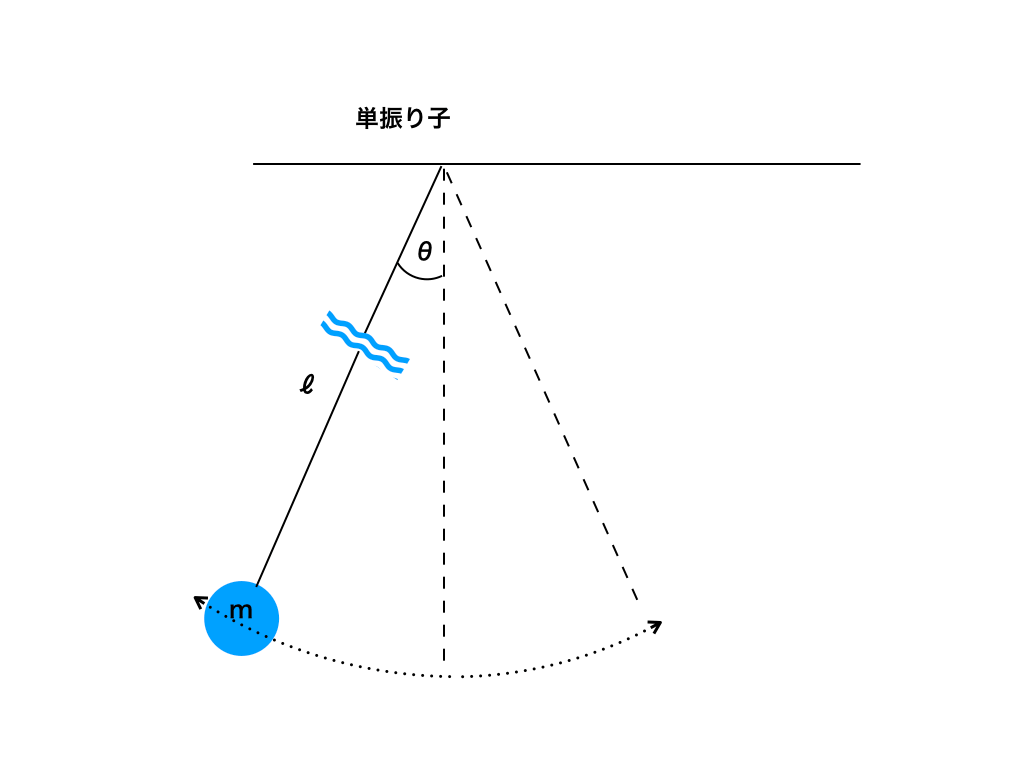
<図1:単振り子のイメージ>
<図1>の様に振り子の糸が非常に長い(あるいはおもりをごく僅かに振らせる)ために、θが非常に小さくなります。
結果として、振り子の運動は近似的に水平方向の単振動とみなすことができます。
単振り子の復元力と運動方程式
ここからは、単振り子を揺らした際におもりが中央に戻ろうとする力(=復元力)と近似の考え方を使って、運動方程式を立てていきます。
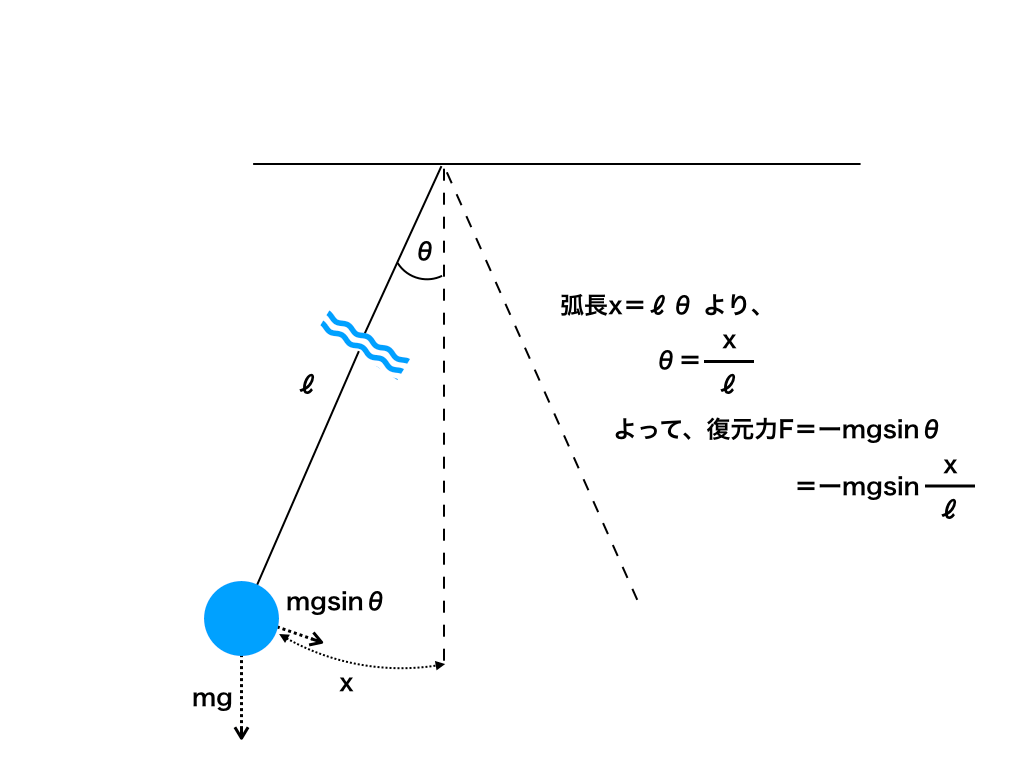
<図2:単振り子を水平方向の単振動と近似する>
ここでsinθを考えてみると、
弧の長さを、x=ℓθ として、$$θ=\frac {x}{ℓ}$$
θが非常に小さいとき、近似的にsinθ≒θとすることができます。
(参考:三角関数のグラフの原点付近を見ると、確かに、y=θとy=sinθ がほぼ同じである事がわかります↓)
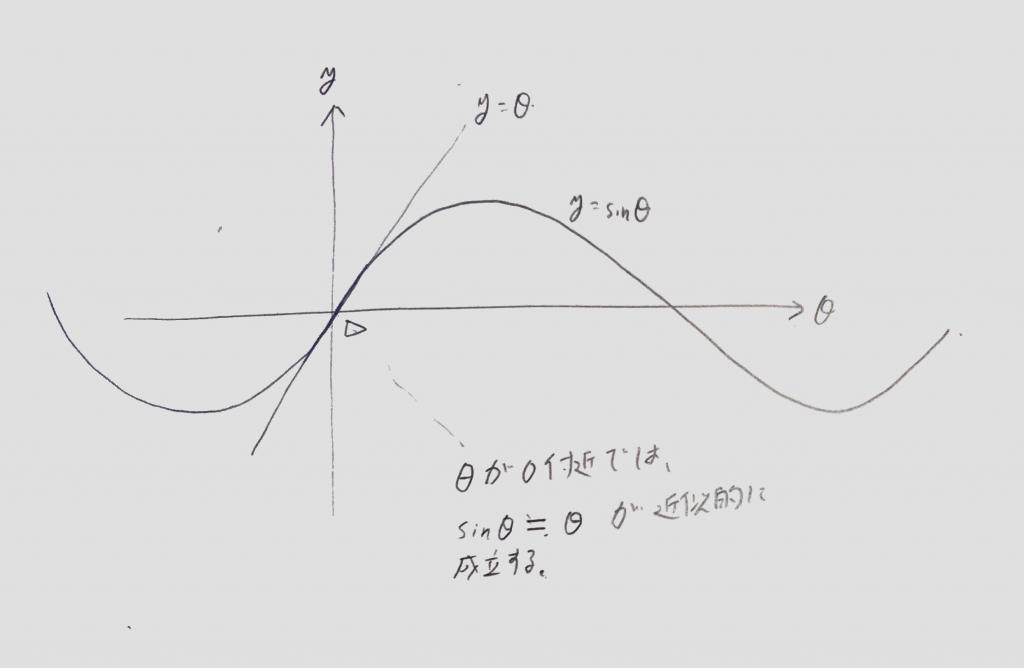
<sinθとθの原点付近でのグラフ>
$$従って、振り子の復元力F=ーmgsinθ≒ーmg\frac {x}{l}$$と書くことができます。
(符号のマイナスについて:復元力は常に中心方向を向くため「ー」がつくことに注意して下さい。)
よって運動方程式は$$ma=-mg\frac {x}{l}$$となります。
運動方程式から単振り子の周期Tを求める
運動方程式が立てられたので、あとは以前からやっている様に、単振り子(単振動)の周期を求めていきます。
忘れてしまった人は→「単振動の周期を求める流れ(単振動第一回)」
$$まずma=-mg\frac {x}{ℓ}より、a=-g\frac {x}{ℓ}$$
角振動数ω(rad/s)を使ってa=-ω2xと比べると、
$$ω=\sqrt {\frac {g}{l}}$$
$$更に、周期T=\frac {2π}{ω}より、$$
$$この単振り子の周期T=2π \sqrt {\frac {ℓ}{g}}と書けます。$$
$$※バネ振り子の周期T=2π \sqrt {\frac {m}{k}}$$
との違いに注意しましょう。
この単振り子の近似から周期を求めるまでの流れは、
暗記するのではなく、理解して自力で導く事が出来る様にしておきましょう。
(白紙に2、3回図1を描いて、周期Tを何も見ずに導出する事が出来ればOKです!)
単振り子と慣性力の確認問題
では、簡単な例題で単振り子と慣性力の融合問題の解き方を確認してみましょう。
(確認例題)
今、加速度αで上昇しているエレベーターの天井から単振り子がつるされている。
この単振り子を僅かに振らせるとき、この単振り子の周期Tを求めよ。
ただし、重力加速度をg、振り子の糸の長さをl、おもりの質量をm、糸の質量は考えないものとする。
<解説>
この様な問題では、自分もエレベーターに乗って、
単振り子の運動を観察する様にします。(エレベーターの外から見ると、運動が非常に複雑になります。
すると、今上向きにαの加速度がエレベーターにかかっているので、
振り子のおもりには下向きに同じ大きさ(α)の加速度が働いている様に、
エレベーターに乗っている人からは見えます。(=慣性力)
さらに、重力加速度gと合わせて、下向きに(α+g)の加速度がかかる事から、
運動方程式は、ma=ーm(g+α)sinθ
以下これまでと同様に、
$$近似的にsinθ≒ \frac {x}{l}と出来るので、$$
$$a=-\frac {(g+α)x}{l}$$
$$a=-ω^{2}x,とT=\frac {2π}{ω}より$$
$$求める周期Tは、T=2π \sqrt {\frac {l}{(g+α)}}$$
まとめと単振動の関連記事
最後の確認例題でも触れましたが、単振り子はそれ単体というよりも、
主に加速度運動しているもの(エレベーターや車、電車など)の中に設置されて、
その周期などを計算する問題が出題されやすいです。
この記事で大体の解き方を理解出来たら、類題を探して解いてみて下さい!
<単振動の関連記事>
単振動第1回「これで解ける!一から始める単振動第一回」
単振動第2回「単振動第二回:摩擦力が働く単振動の問題」
単振動第3回:今ここです
単振動第4回「浮力とは?そして単振動との融合問題」
今回も最後までご覧いただき有難うございました。お役に立ちましたら、
シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせは、
コメント欄又はお問い合わせページまでお願い致します!

