
万有引力/宇宙速度/ケプラーの法則解説シリーズ(3)
今回は、ケプラーの第一・第二・第三法則と、関係する数学Ⅲの楕円の性質を解説します。
以下の2記事 +この記事でケプラーの法則と万有引力の基礎はバッチリ身につきます!
第三回:ケプラーの3法則と楕円<今ココです>
目次(タップした所へ飛びます)
ケプラーの法則導入:楕円の性質(数Ⅲ)
ケプラーの法則の解説に入る前に、簡単に「楕円」について紹介しておきます。
範囲は数学Ⅲの「式と曲線」ですが、理系ならば必須の内容なので未習の人も目を通しておいてください。
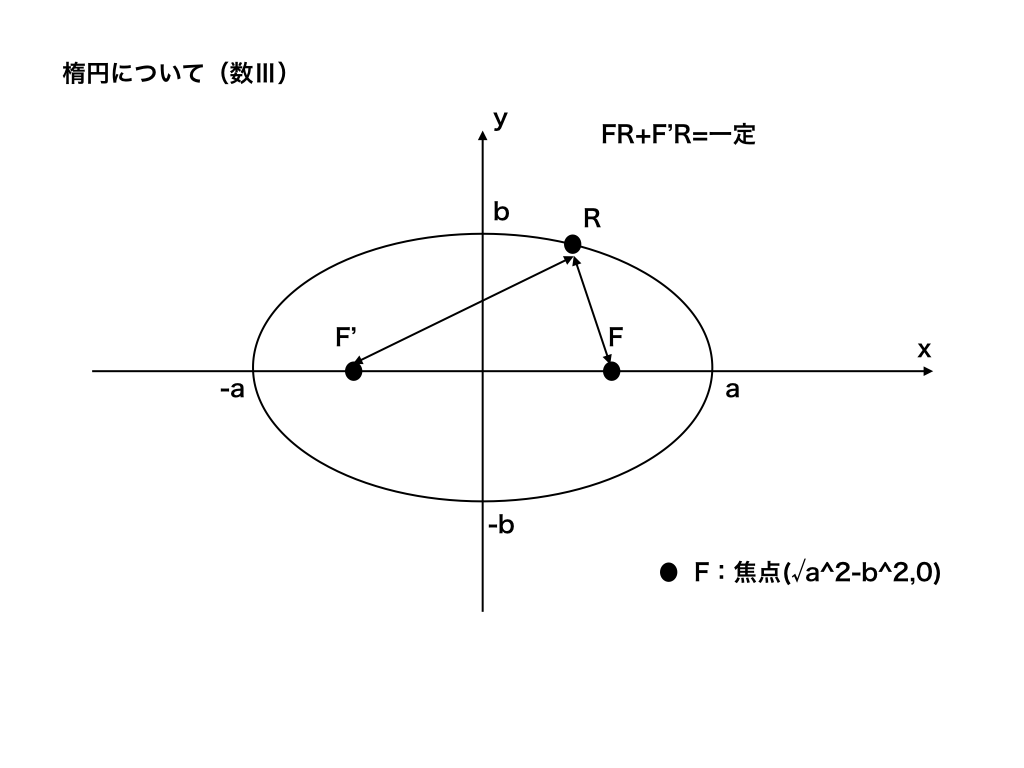
さて、楕円とは<図1>の様な形をした曲線で、
「焦点:F(Focus)と呼ばれる2つの点と、その2点以外の点との(仮に点Rとします)の距離の和が一定である点の軌跡」です。
もう少し簡単に言うと、「FR +F‘R=一定」になる点Rを無数に描いた時に現れる曲線のことです。
<図1:楕円>
楕円にはいくつか知っておくべき性質があります。
<図1>の楕円が、原点を中心にしているとすると、(aから-a)の方が(bから-b)までの長さより長くなっています。
この時、(a,0),(-a,0)間を長軸、(0,b),(0,-b)間を短軸と言います。
さらに、(a,0)から(0,0)までのことを半長軸、その長さのことを長半径と呼びます。
これはケプラーの法則で頻繁に出てくるので覚えておきましょう。
ちなみに、焦点の座標はそれぞれ:焦点FとF'の座標\(( ±\sqrt {a^{2}-b^{2}},0) \)
となります。さらに詳しくは数学3「式と曲線(二次曲線)シリーズ(楕円)」で紹介していきます。
ケプラーの第一・第二・第三法則とは
では、ここからケプラーの3法則をそれぞれ解説していきます。
ケプラーの第一法則(楕円軌道上の運動)
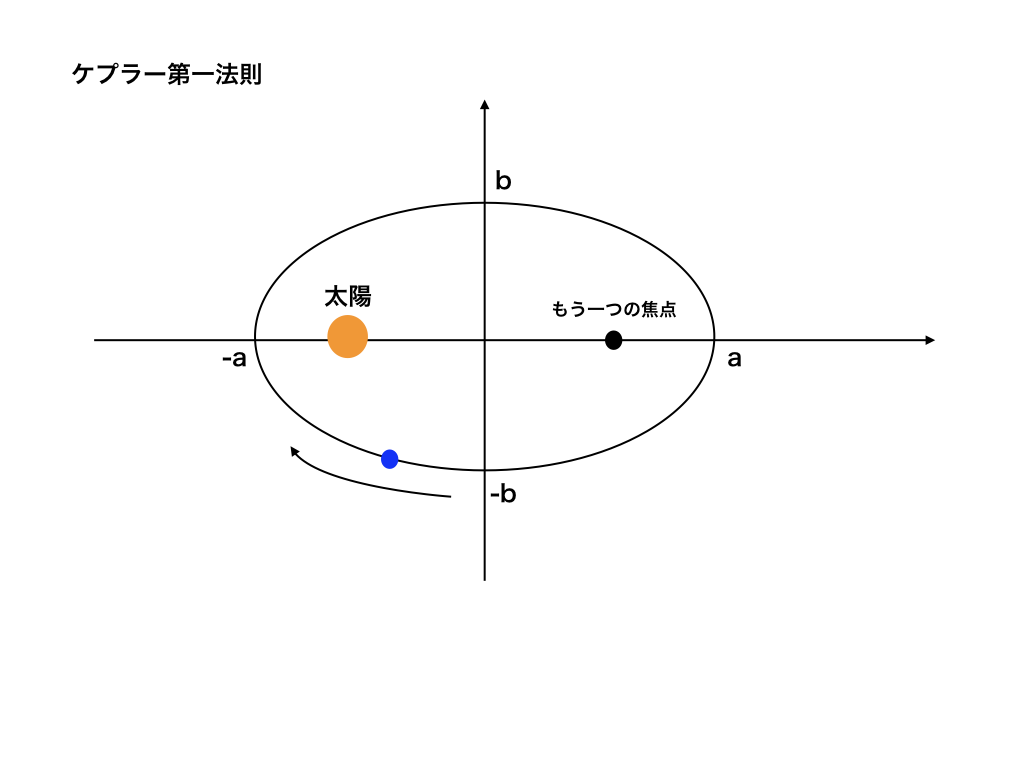
ケプラーの第1法則は、「惑星は、太陽を焦点の一つ(F)とする楕円軌道上を動く」と言うものです。→<図2>
<図2:ケプラーの第一法則(太陽を焦点の1つとする楕円)>
ブルーで楕円(軌道)上を動いているのが惑星です。
この法則は、地球だけではなく火星や金星、土星など全ての惑星に当てはまります。
ちなみにもう一つの焦点には特に何も存在しません。この第一法則は知識としてもっておいて下さい。
ケプラーの第二法則(面積速度一定の法則)
第二法則は、別名「面積速度一定の法則」ともいい、惑星がケプラーの第一法則の通り運動している時、
単位時間(例えば1秒や1年)で動いた距離と、
太陽を結んだおうぎ形の面積が常に同じである!と言うことを言っています。
<図3:面積速度一定(角運動量保存則)>
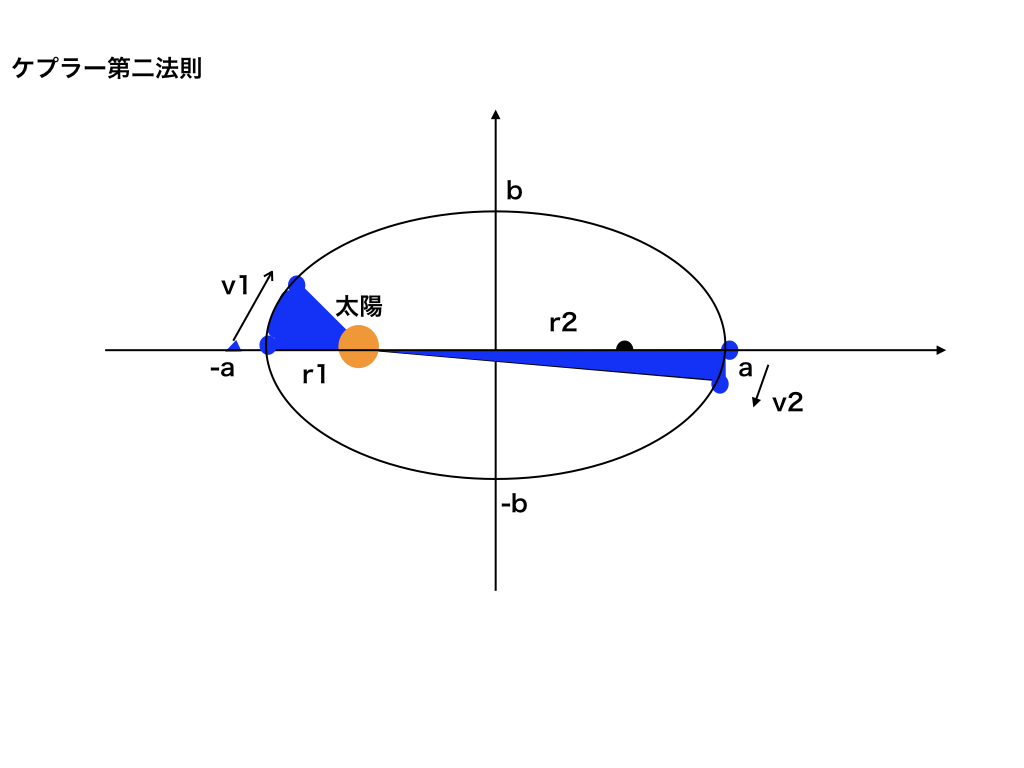
<図3>を見て下さい。
『(ーa)から速度v1で進んだ太陽からの距離がr1の扇型の面積』=『(a)からv2で進んだ太陽からの距離がr2の扇型の面積』このように、2つの扇形の面積は同じになります。
また、扇形の面積は単位時間が非常に小さい時、r1を底辺、v1を高さにした三角形の面積に近似でき、同様にr2を底辺、v2を高さにした三角形の面積に近似できます。
これを式で表すと、
$$\frac {1}{2}r_{1}v_{1}=\frac {1}{2}r_{2}v_{2}$$
となります。
この面積が一定である法則(面積速度一定の法則)は同一の惑星で、同一時間(単位時間)運動したものであれば、いつでも成り立ちます。
つまり、惑星が太陽に近いところを通っていればその分速度が大きく、太陽より遠いところにいるときは速度が小さくなっているのです。
(※:もし太陽に近いところで速度が小さければ、扇型の面積はより小さく、遠いところで速度が大きければ面積がより大きくなってしまい、一定にはなりません!)
(+α):高校範囲外になりますが、この面積速度一定の法則は様々な運動で成り立ち、「角運動量保存則」と言う名前がついています。
興味のある人は調べてみて下さい。
ケプラーの第三法則
ケプラーの第3法則とは、惑星の公転周期をT、楕円の長半径をaとした時、
\(\frac {T^{2}}{a^{3}}\)
が常に一定となると言う法則です。
$$\frac {T^{2}}{a^{3}}=k (k=一定)$$
例えば、地球の公転周期は1年、
地球が運動する楕円軌道の長半径は およそ1.5×108(km)
木星の公転周期は11.9年
木星が運動する楕円軌道の長半径はおよそ7.8×108(km)
実際に計算してみると、
地球が3.375
木星が3.351
と、確かにほぼ同じになります。
ケプラー3法則と万有引力の確認問題
これまでの「万有引力の法則〜ケプラーの法則」3回のまとめとして、定着用の問題を作りました。
一題で基礎的なことが色々と問えるので、(数字などは違えども)似た問題は超頻出です。
定着問題
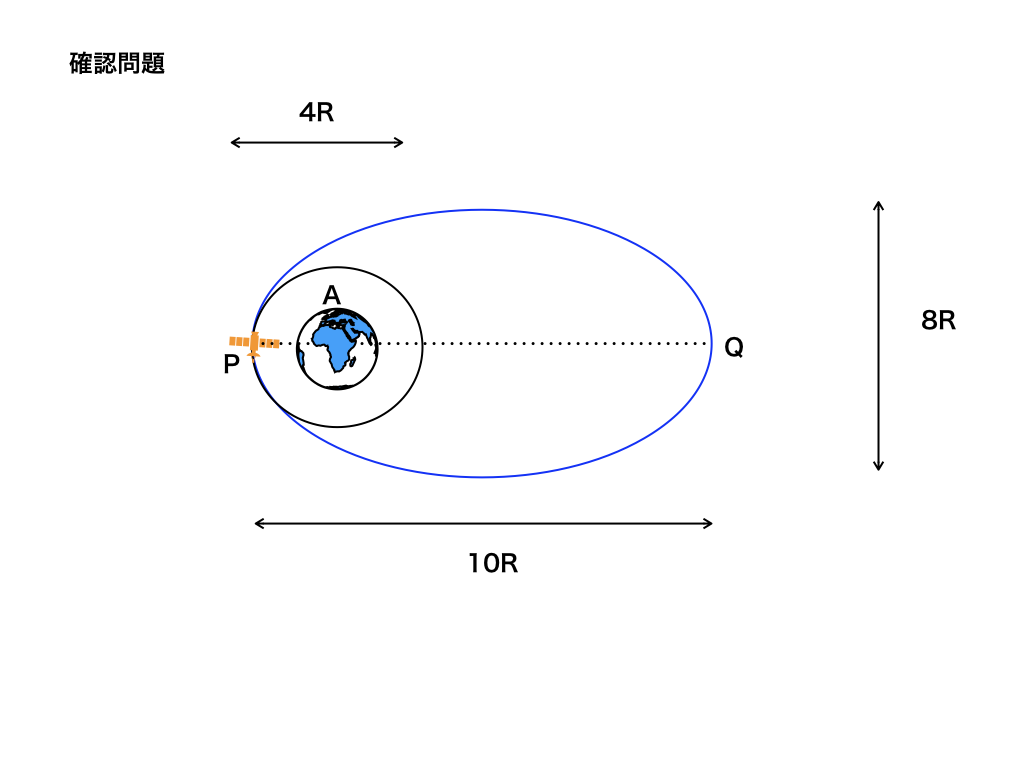
今、<図4>の惑星Aを中心に人工衛星が速度v1で円運動している。
その後、周回軌道上の点Pで衛星を速度vpまで加速させると、
青色で示したAを焦点の一つとする楕円軌道上を運動し始めた。
万有引力定数をG、惑星Aの質量をM、人工衛星の質量をm、惑星の半径をR、とするとき
問1:人工衛星の速度v1を求めよ。
問2:加速後の点Pでの速度vpはv1の何倍かを求めよ。
問3:<図4>上に示した点Qでの人工衛星の速度vqを求めよ。
問4:青色の楕円軌道の周期T‘を求めよ
<図4:ケプラーの法則まとめ問題図>
解答解説
問1:惑星Aを中心とする円運動
見直したい人は「第一宇宙速度と万有引力を向心力とした円運動」を読んでみて下さい!
<図4>より、惑星の半径がRで、円軌道の直径が4Rなので、
万有引力をF(ここでのFはforce:力です。念のため)とした運動方程式が書けます。
$$\frac {GMm}{( 2R) ^{2}}=m\times \frac {v^{2}_{1}}{2R}$$
$$\frac {GM}{2R}=v^{2}_{1}$$
$$したがって、v_{1}=\sqrt {\frac {GM}{2R}}$$
問2:ケプラーの法則に本格的に入っていきます。
まず<図4>から読み取れるのは、長半径が5Rで短半径が4R、更に円軌道の直径が4Rである事です。
このタイプの問題の解き方は、「ケプラーの第2法則と、力学的エネルギー保存の式を連立させる」というほぼワンパターンです。
実際に立式していきます。
ケプラーの第二法則(面積速度一定)より、
$$\frac {1}{2}(2R)(v_{p}) =\frac {1}{2}(8R)(v_{q}) ,,,1$$
力学的エネルギー保存則より、
$$\frac {m}{2}v^{2}_{p}+( -\frac {GMm}{2R}) =\frac {m}{2}v^{2}_{q}+( -\frac {GMm}{8R}) ,,,2$$
1式より、vp=4vq ・・・3
2式より、$$\frac {v^{2}_{p}}{2}-\frac {v^{2}_{q}}{2}=\frac {GM}{2R}-\frac {GM}{8R},,,4$$
4式を整理して、$$v^{2}_{p}-v^{2}_{a}=\frac {3GM}{4R},,,5$$
5式に3式を変形した\(v_{q}=\frac {v_{p}}{4}\)を代入して
$$\frac {15}{16}v^{2}_{p}=\frac {3GM}{4R}$$
$$v^{2}_{p}=\frac {4GM}{5R}$$
$$v_{p}=\sqrt {\frac {4GM}{5R}}これでv_{p}が$$
表せたので、(問1)のv1と比べてみると、
$$v_{1}=\sqrt {\frac {GM}{2R}}$$
$$\frac {2}{\sqrt {\frac {5}{2}}}=\frac {2\sqrt {2}}{\sqrt {5}}=\frac {2\sqrt {10}}{5}$$
$$よって、v_{p}はv_{1}の\frac {2\sqrt {10}}{5} 倍である$$
問3:面積速度一定の法則を使います。
これはケプラーの第2法則と、問2で計算したvpからすぐに計算出来ます。
面積速度一定(ケプラーの第2法則)より、
$$\frac {2R×v_{p}}{2}=\frac{8R×v_{q}}{2}$$
よって、\(v_{q}=\frac{v_{p}}{4}\)
$$問2より、v_{p}=\sqrt {\frac {4GM}{5R}}だから$$
$$v_{q}=\sqrt {\frac {GM}{20R}}$$
問4:ケプラーの第三法則の総まとめ問題
ケプラーの第3法則とは、
$$\frac {惑星の公転周期Tの2乗}{楕円の長半径aの3乗} でした。$$
これをを利用します。
円には長半径はありませんが、ふつうに半径を代入して問題ありません。
$$\frac {T^{2}}{(2R) ^{3}}=\frac {(T')^{2}}{(5R)^{3}}$$
$$⇔\frac {125T^{2}}{8}=(T') ^{2}$$
元々の円運動の周期は右の式で表せるので、
$$T=\frac {2\pi(2R) }{v_{1}}$$
$$\frac {125}{8}× ( \frac {4\pi R}{v_{1}})^{2}=(T') ^{2}$$
$$ここで、v_{1}=\sqrt {\frac {GM}{2R}}より$$
$$\frac {125×16\pi ^{2}R^{2}}{8\times \frac {GM}{2R}}=(T')^{2}$$
$$⇔ \frac {500\pi ^{2}R^{3}}{GM}=(T') ^{2}$$
$$⇔ T'=10\pi R\sqrt {\frac {5R}{GM}}$$
よって、$$T'=10\pi R\sqrt {\frac {5R}{GM}}$$が答えになります。
万有引力、ケプラーの法則、宇宙速度シリーズのまとめ
これまで見てきた様に、高校物理で出てくる”万有引力やケプラーの法則”の問題は、一見すると難しそうですが、ある程度パターンが決まっています。
上の確認問題が4つができればかなり基礎は固まっているので、あとは類題を見つけて解いて行って下さい。
(難関大学でなければ、過去問にそのまま繋げることも可能です)
宇宙速度シリーズ一覧&関連記事
第三回:ケプラーの3法則<今ココ>
<難関大/学部を目指す人へ>
この単元は良く単振動との融合問題が出題されます。
更に上を目指すなら、→「単振動を徹底解説」で通常の単振動の解き方と、
微積分を使った説明を載せています。ぜひご覧ください。
今回も最後までご覧いただき有難うございました。お役に立ちましたら、
シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・その他のお問い合わせはコメント欄までお願い致します。

