
高校物理/物理基礎の電磁気分野の総まとめページ【更新中】
<このページの内容>:電流の基礎(電子との関係など)から、高校物理で必須の法則・公式などを解説した記事のまとめページです。
基礎の基礎から難関大の過去問が解けるレベルまで、随時記事を追加していきます。
(更新:「サイクロトロン」および「演習の仕方(オススメの問題集)」の記事を追加しました。)
↓↓【タップ・クリック出来る目次】↓↓
目次(タップした所へ飛びます)
電気分野
まずはじめは、『電流』の意味と、回路問題を解く際に必須の法則を紹介します。
電流とは?I=envSの式 ~オームの法則まで
そもそも電流とはどのようなものなのか?
非常に小さな世界での電子の振る舞いを考えて、電流の式:”I=envS”を導きます。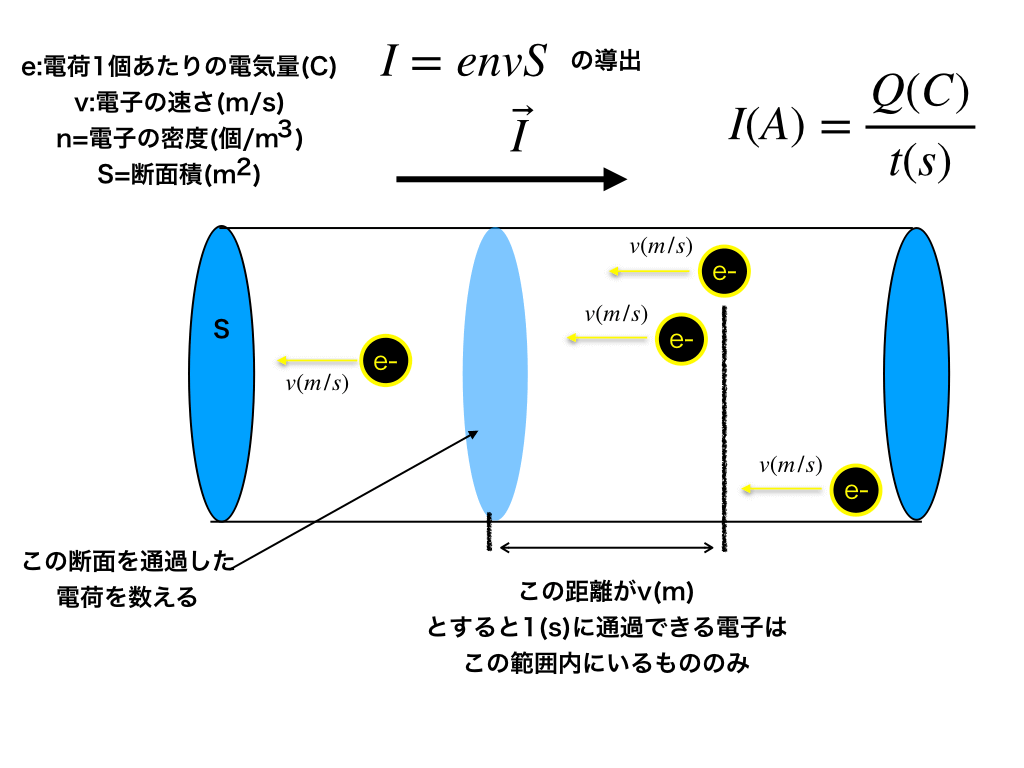
後半ではV=IRで表されるオームの法則と、電子の移動する向きと電流が”逆向き”になっている理由を「I=envSの式からオームの法則・電流の正体まで」<の記事で解説しています。
(消費)電力Pと応用問題
「消費”電力”の基礎から公式・有名問題の解法まで」で(消費)電力Pと、それを利用する”Pmax”を求める”可変抵抗の問題”や、”熱力学との応用問題”の解き方を紹介しています。
非線形抵抗の問題とグラフ上の交点
上の項で解説したオームの法則は、線形(電流”I”と電圧”V”が比例の関係)にありました。
しかし、電球などの必ずしもオームの法則に従わない装置が回路に含まれている場合があります。
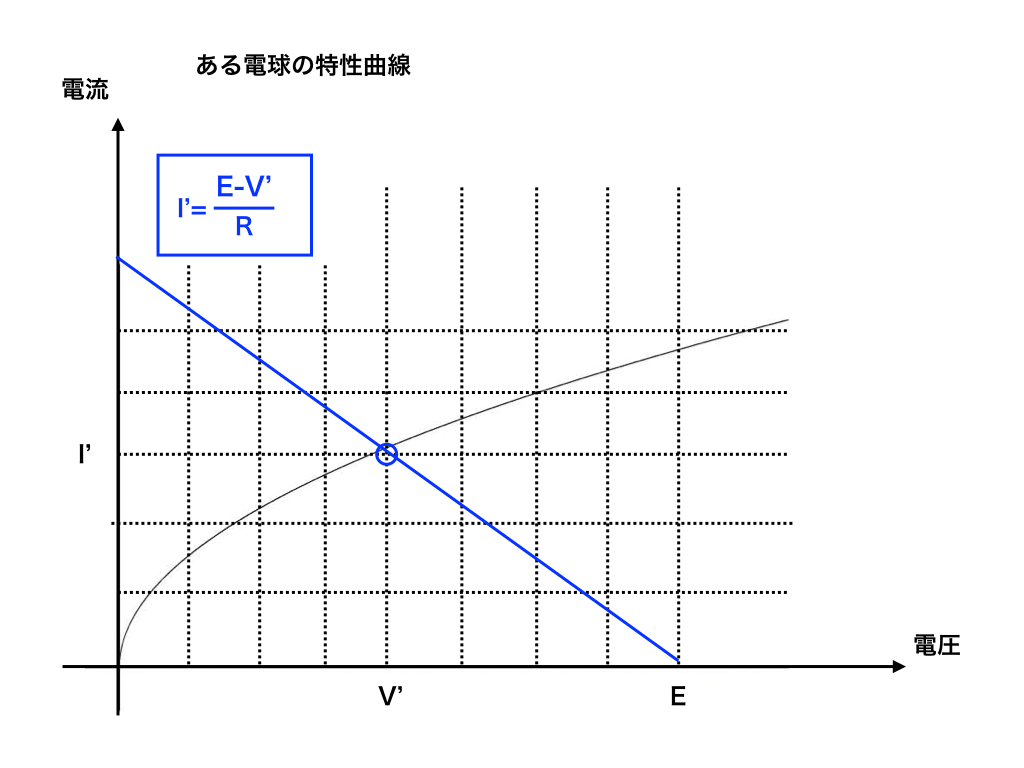
すなわちI=Vグラフが比例にならない(=非線形)の抵抗となります。
そのような非オーム(線形)抵抗が回路に含まれている場合の解法を「非オーム抵抗の問題と、特性曲線との交点が解になる理由」で詳しく紹介しました。
キルヒホッフの法則
電気回路の問題を解くためには必ず必要になる
・キルヒホッフの”第一”法則:流れ込む電流の総和=流れ出す電流の総和
・キルヒホッフの”第二”法則:閉回路を一周した時の電圧の総和=0
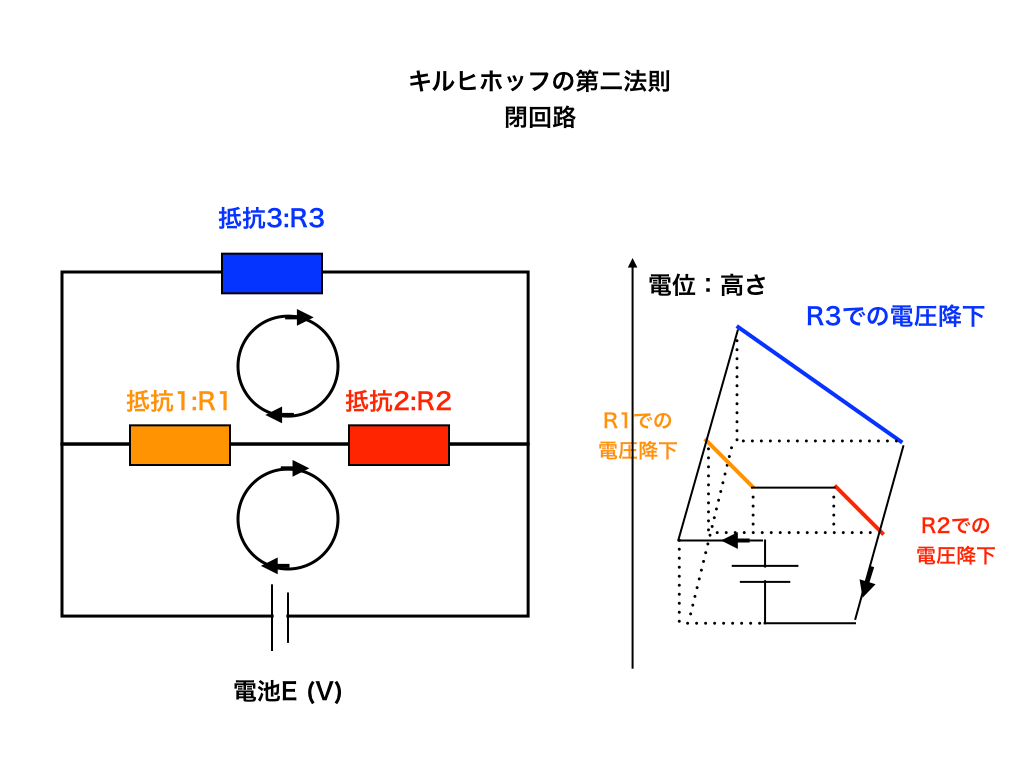
について、それぞれ「キルヒホッフの第一・第二法則とその使い方」で解説しました。
コンデンサーの仕組みと電気容量
回路の問題で頻出の”R(抵抗)”、”L(コイル”)”,C(コンデンサ)”のうち、ここではコンデンサーについて扱います。
「コンデンサーの仕組みと公式の意味」では、二枚の金属板からなるコンデンサーが電気を蓄えることができる仕組みや、コンデンサーに関連する諸公式・電池のした仕事などを解説しました。
電気容量を変化させる方法
次に、電気容量(F)の式$$C=ε\frac{S}{d}$$と、その値を変える方法について「コンデンサーの電気容量を変化させる4つの方法」で理解を深めましょう。
コンデンサーを含む電気回路の問題(基礎編)
仕組みがある程度理解できたら、次は電源をつなげた回路の問題を実際に解いていきます。「コンデンサ回路の問題例とその解き方(基礎)」<<
スイッチを切り替える問題(コンデンサー回路応用:作成中)
次に、難関大頻出である”回路にスイッチが含まれている”回路の解法を「スイッチを切り替えて電気量が変化する応用問題(作成中)」で紹介します。
ダイオードとpn型半導体
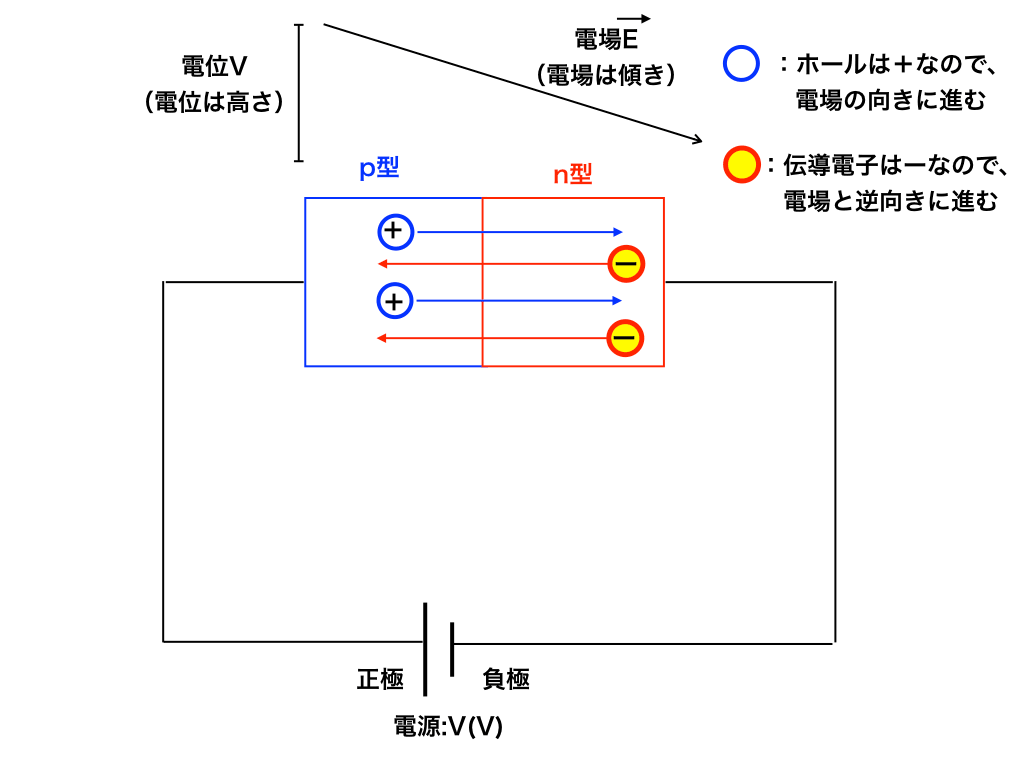
一部高校レベルの化学の基礎知識を用いて、半導体とcarrier、ダイオードについて解説しました
クーロンの法則やガウスの法則など(応用)
ここまでの記事では、主に電気回路の問題を解くための”具体的な”方法や考え方を解説してきました。
この項では点電荷どうしに働く力や、電荷と電場・電位の関係などの意味を掘り下げる少し応用分野に入っていきます。
(電)磁気へ進む前に、それぞれの意味を整理しておきましょう。
クーロンの法則と点電荷が作る電位・電場の意味
点電荷の間に働く力である”静電気力=クーロン力”と、その大きさを求める”クーロンの法則”。
さらにその点電荷が作る電場・電位のイメージについて「クーロンの法則と電位・電場の違いをイメージする」で紹介しました。
点電荷と力学の融合問題の解法
上の項で求めた”点電荷の作る電場や電位”を利用し、点電荷の運動を考える「複数の点電荷による座標上の電位・電場と力学の融合問題」の解き方の記事です。
ガウスの法則とは?
コンデンサーの容量などの公式でも頻繁に現れる、”ε(誘電率)”の意味などを”ガウスの法則”を用いて考えていきます。「ガウスの法則とは?電場・電気力線との関係をイラストでわかりやすく解説!」<<
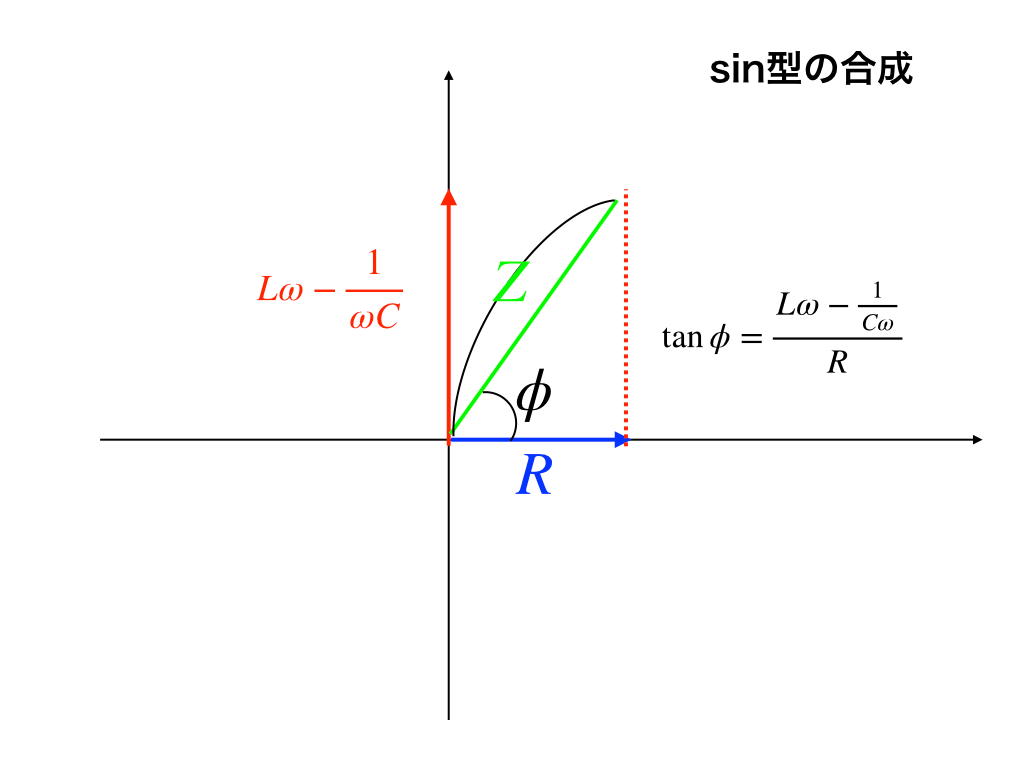
交流とRLC回路・インピーダンス
交流電源と接続したR/L/C直列回路について、三角関数の微分と合成を用いて解説しています。
「”RLC”直列回路とインピーダンスの意味・式、位相をわかりやすく!」
続編(電気振動)を作成中です。2019/10/16
作成済み
電気振動(LC回路)と共振とは
コイルL・充電済みのコンデンサーCをつないだ回路での”電気振動”と、「RLC回路」における『共振』について「電気振動と共振周波数の求め方」で解説しています。
磁気分野
電気分野と密接に関連し、公式などの類似点も多い『磁気分野』について以下の記事でまとめていきます。
電流が作る磁界
この「電流と磁界をわかりやすく!」の記事では、電流が流れることによって生じる磁界《3タイプ》の方向と、強さの計算方法をイラストを用いて紹介しています。
フレミングの法則と電磁力・ローレンツ力
・「フレミングの左手の法則と電磁力・ローレンツ力」”フレミング左手の法則”を用いて
・『電磁力』や
・『ローレンツ力』の向きを調べ、それぞれの大きさの求め方を解説しています。
荷電粒子の運動(ローレンツ力問題編1)
上の記事で紹介した”ローレンツ力”を使って、荷電粒子の運動を調べる問題編:「ローレンツ力と荷電粒子(1)」を作成しました。
力学と電磁気学を融合させた基本的な問題を扱っています。
加速器(サイクロトロン)
ローレンツ力の応用(2)として、電子を加速する「サイクロトロンの仕組みと問題の解き方」を解説しました。
電磁誘導
電磁誘導の基本となる「コイルの性質などの基礎編」
と
力学と融合した「右手の法則と導体棒の運動」
をそれぞれ作成しました。
・・・
現在作成中です。もうしばらくお待ちください。
電磁気分野と関係のある記事(付録)
ここでは、電磁気以外の分野であっても知っておくと役立つ、力学や高校数学の記事と演習の仕方の記事を付録としてまとめました。
切り替え問題などで使う漸化式(数学B)や極限(数学Ⅲ)
電気回路において、スイッチを切り替える問題では、『漸化式を作って一般項を求める。』という作業をすることがあります。
そのために必要な知識を「漸化式の解き方全12種類総まとめ」で、また”無限回の操作”を行った時、一般項の極限をとる際に必要な知識は「数3の極限分野をわかりやすく!」で紹介しています、
クーロンの法則と万有引力の公式
どちらの公式も非常に似た形をしています。
2つを見比べると色々と面白い発見があるかもしれません。
等速円運動と単振動(融合問題で利用します)
力学の範囲ですが、荷電粒子がこれらの運動を行うことがあります。特に難関大の志望者のかたは必見です。>>「単振動をわかりやすく!等速円運動と微積使用・不使用の両方で解説」<<
基礎を習得したら即演習【おススメ問題集5選】
・この記事+関連記事で学んだ基礎知識を、
・実際に入試問題を解くことができる様になる為に適した(レベル別の)演習本を5つ選び、まとめて紹介しました。
・・・
今回も最後までご覧頂きまして、有難うございました。
また、お役に立ちましたら、B!やシェア、Twitterのフォローをしていただけるとたいへん励みになります。
・その他のお問い合わせ・ご依頼等に関しましては、ページ上部【運営元ページ】からご連絡下さい。

