サイクロトロンの仕組み(電磁気/原子分野)
<この記事の内容>:高校物理:電気・磁気の各分野と力学分野の”まとめ的”な問題である、『加速器』特に「サイクロトロン」の仕組みと問題の解き方を解説しています。
(+α:シンクロトロン、次回のベータトロンへつなげるための付録付き)
>>「高校物理:電磁気分野を総まとめ!」<<
↓↓タップ/クリックで飛べる目次↓↓
目次(タップした所へ飛びます)
サイクロトロンとは
まずはサイクロトロンが含まれる『加速器』の”種類や仕組み”を簡単にまとめ、次の(問題編)でより詳細な内容を身につけていきます。
加速器の目的
加速器とは、その名の通り電子をはじめとする『粒子』を電磁気の力を用いて、徐々に速度を上げていく装置(機械)のことを言います。
後述しますが、加速するにつれて粒子の持つエネルギーが増大し、それを原子(やそれを構成する粒子、素粒子など。)にぶつけてその中身を調べるなど、現代の科学に無くてはならないものです。
種類と仕組み
加速器の主な種類には
・サイクロトロン
・シンクロトロン
・ベータトロン
があります。
高校範囲+αのレベルでは、上の三つを簡単なモデルにした問題が出題されます。
(理解のための基礎/関連知識)
今回の【サイクロトロン】の問題では、『ローレンツ力+円運動』の知識が必須なので、あやふやな人は以下の記事を参考にしてください。
サイクロトロンの問題編
ではここからさらに具体的に、かつ詳しく例題を使って説明していきます。
例題:荷電粒子の加速
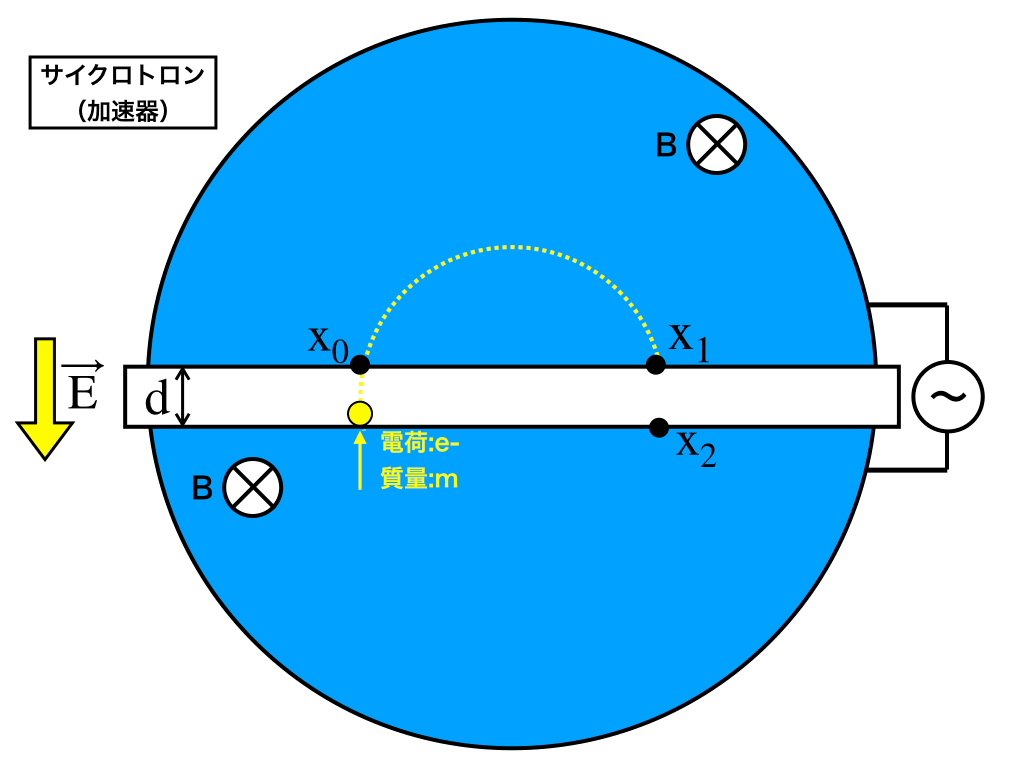
いま以下の【図1】のような半円状の2つの極板を設置し、一定のタイミングで電流の流れの向きが変化する交流電源を取り付けた。
(極板どうしの間には非常に狭い隙間:d(m)があり、交流電源により電場\(\vec{E}\)の向きが変化する。)
画面手前から奥方向へ磁場B(T)が発生しており、電荷\(e^{-}\),質量mの電子が初速度\(v_{0}でx_{0}\)に入った。
問1:電子はローレンツ力により、\(x_{0}からx_{1}\)まで円運動する。
・この時の向心力と\(|x_{0}x_{1}|\)間の距離を求めよ。
問2:電子が\(x_{1}\)からから飛び出すと同時に、電流の向きを逆転させて、上側の極板から下側の極板に電場\(\vec{E}\)がかかるようにした。
・この時、\(x_{1}からx_{2}\)の(隙間dの)間で、電子が得たエネルギーを求めよ。
問3:\(x_{2}\)に入射した電子は、速度\(v_{1}で\)再び円運動を起こして\(x_{3}\)に達する。
・この時電子は『時計回り』と『反時計回り』のどちら向きの運動をするか。
・また、その円運動の直径と電子の速度を求めよ。
問4:これをn回繰り返した時、電子が持つ力学的エネルギーはいくらになるか。
次の\(n,v_{0},B,e,m\)を用いて答えよ。
【図1】
解答解説:ローレンツ力とサイクロトロン
段階を踏んで一つ一つ解いていきましょう。
解説(1):荷電粒子の運動
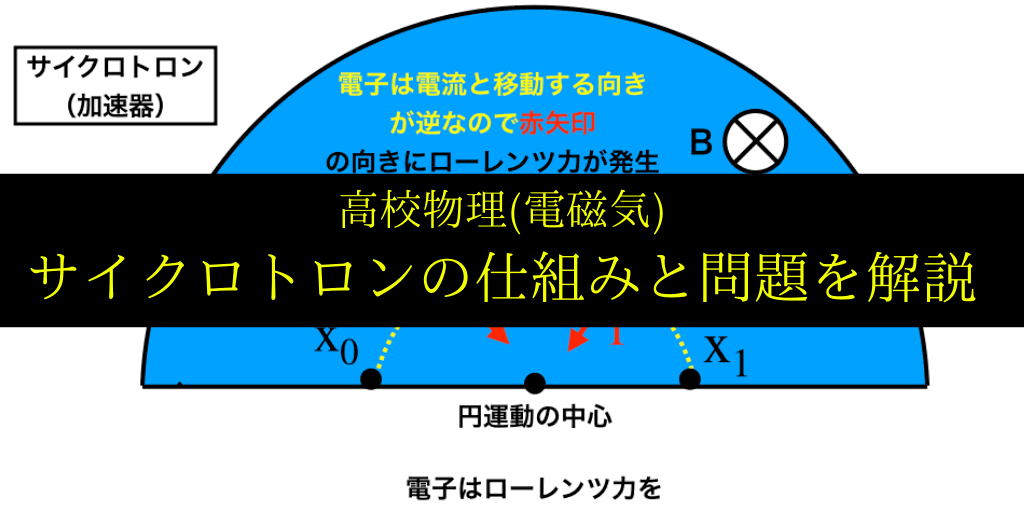
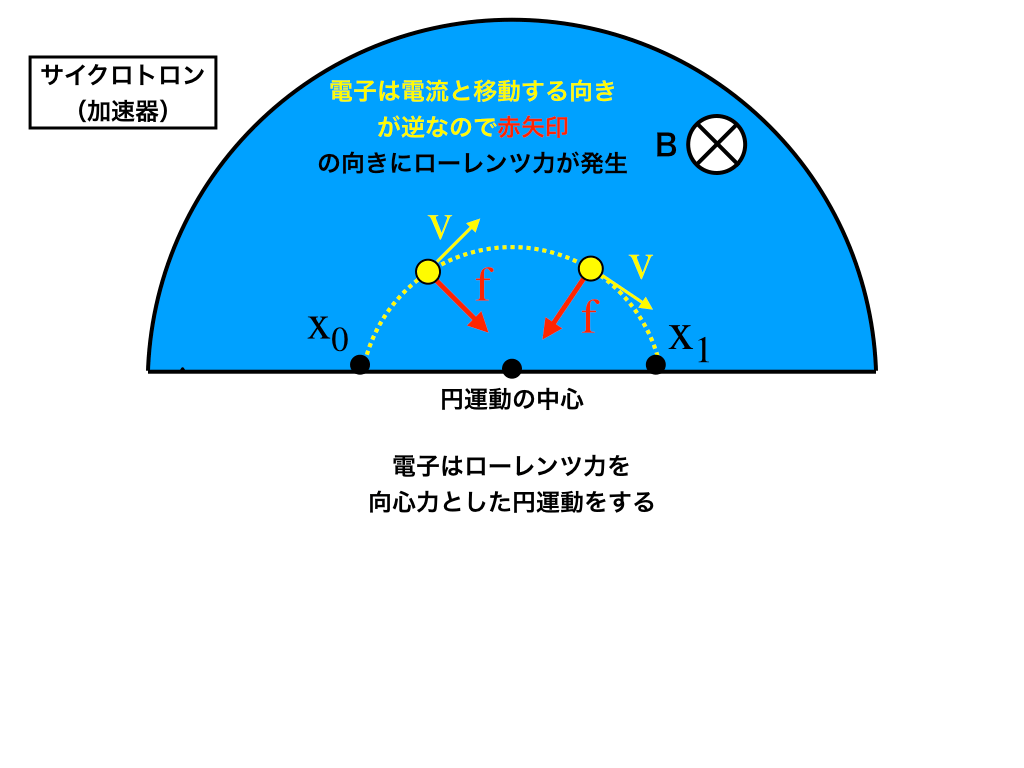
問1では、まず【図2】のように、\(|x_{0}x_{1}|\)を直径とする円運動を調べます。
\(f_{ローレンツ力}=v_{0}Be\) を向心力とする円運動を行う・・・(答1-1)ので、
$$m\frac{v_{0}^{2}}{r}=v_{0}Be \leftrightarrow r=\frac{v_{0}m}{Be}$$
したがって半径rの二倍が求めたい直径より、$$|x_{0}x_{1}|=2\frac{v_{0}m}{Be}$$・・・(答1-2)
【図2】
解説(2),(3):二回目の円運動
次に、\(x_{1}をv_{0}\)で飛び出した電子は電場\(\vec{E}\)により加速されます。
ゆえにこの間電子が得たエネルギーは\(e\cdot E\cdot d=eEd(J)\)・・・(答2)
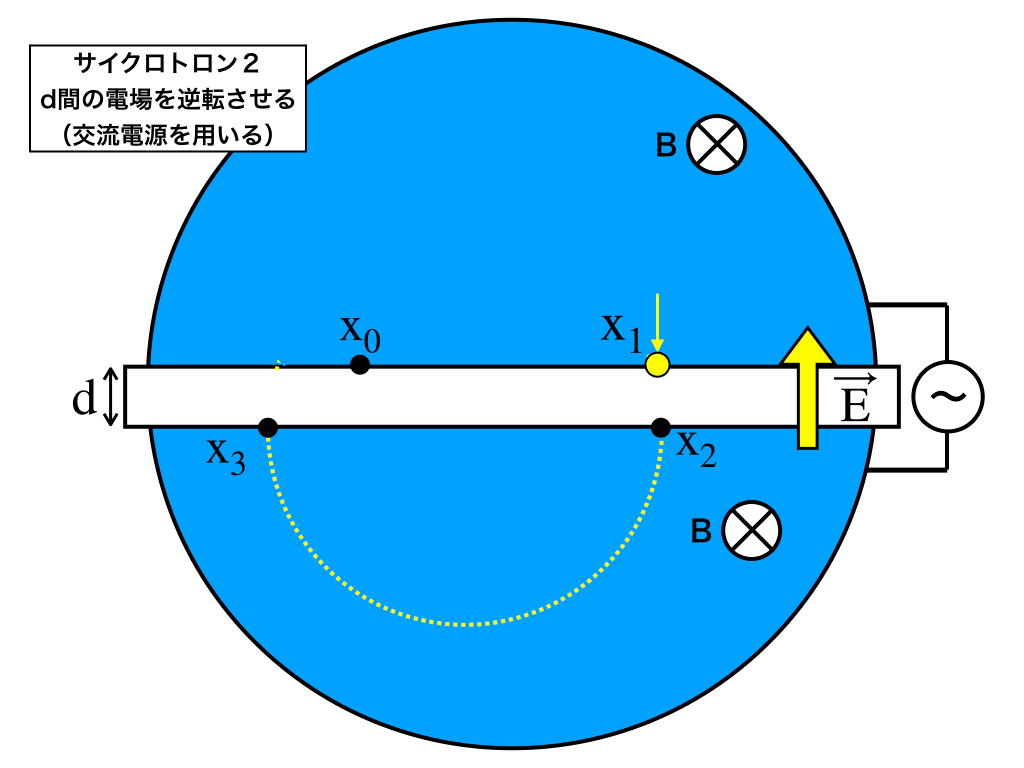
そして、この電子が\(x_{2}\)に入ってきます。
今度は電子の移動方向が先ほどと逆なので、フレミングの法則より、\(f_{ローレンツ力}\)は先ほどと逆向き、すなわち\(x_{2}→x_{3}\)の向きに発生します。
この時、電子の速度は(答2)と『仕事とエネルギー』の関係を使って、
$$v_{1}=\sqrt{v_{0}^{2}+\frac{2eEd}{m}}$$
そして、以下の【図3】のとおりに向心力が極板の中央へ向いているので、『時計回り』で円運動を起こします。・・・(答3-1)
次に、その半径\(R_{2}\),をこれまで同様に(ローレンツ力)=(向心力)の式から導きだします。
$$m\frac{v_{1}^{2}}{R_{2}}=e\cdot B\cdot v_{1}$$
\( R_{2}\)について整理すると、$$R_{2}=\frac{m}{eB}\cdot v_{1}$$
\(v_{1}\)を上の式に代入し、
\(R_{2}\times 2=|x_{2}x_{3}|\)だから、$$|x_{2}x_{3}|=\frac{2m}{eB}\sqrt{v_{0}^{2}+\frac{2eEd}{m}}$$・・・(答3−2)
【図3】
解説(4):n回後のエネルギー
解説(2)で扱ったように、一回"d"の隙間を通る毎にeEd(J)分のエネルギーが増加していきます。
よって、n回後は、\(n\times eEd=neEd(J)\)・・・(答4)
シンクロトロンversion
サイクロトロンは、上の例題で見たようにだんだんと荷電粒子の回転半径が大きくなっていきます。(そのうち粒子が外へ飛び出してしまう)
その点を改善したものが『シンクロトロン』です。
磁束密度B (T)の大きさを変化させることによって、回転半径を一定の大きさにコントロールします。
(シンクロトロンの問題も、基本的に今回のサイクロトロンの問題の解法と同様にすれば解くことが可能です)
付録:有名な施設など〜リニアコライダーへ
”CERN”は世界最大規模のシンクロトロンを保有している(巨大な円型の装置なので、加速器はスイスとフランスの国境をこえて設置されています)。
(※:因みにWWW(今のワールドワイドウェブ)が発明されたのも、このCERNです!)
最近では、円形加速器だけでなく『リニアコライダー』と呼ばれる、線形(まっすぐな)加速器の利用が検討されており、日本でも岩手県に日米欧が共同してILCを設置する計画があります。
加速器とその問題まとめ
さて、ここまで”サイクロトロン”をメインとした”加速器”を扱っていきましたが、
基本的に
・円運動と
・ローレンツ力
の融合問題に過ぎないことが分かって頂けたでしょうか。
適度な難易度で、力学・電磁気を問うことができる良問なので、しっかり身につくまで何回か復習をしておいてください。
もし、それぞれの分野で不安なところがあれば、よく見直しましょう。
関連する電磁気・原子分野の記事へ
(加速器2):「作成中:ベータトロンの原理と応用問題」
>>「電磁気分野のカテゴリーへ」
>>「原子分野のカテゴリーへ」
最後までご覧いただき、ありがとうございました。
「弊サイト:【スマナビング!】」では、読者の方のご意見・ご感想の募集(全てに対応出来ない場合もございます)をコメント欄にて行なっております。
また、お役に立ちましたらB!やシェアをしていただけると、とても励みになります。
・《お問い合わせ/ご依頼/その他のご連絡》は、ページ上部の【運営元ページ】よりお待ちしております。

