二次曲線シリーズ第3回:楕円
<この記事の内容>:「二次曲線(1)円錐との関係と放物線」/「二次曲線(2)双曲線の方程式」の続編です。
今回は、3つ目の二次曲線である『楕円』の式とその導き方、面積公式、接線の求め方などをイラストを使いながら解説していきます。
目次(タップした所へ飛びます)
楕円
最後は楕円を扱います。高校物理のケプラーの法則の所でも見かけた方もいるのではないでしょうか?→「宇宙速度とケプラーの第1/第2/第3法則」
※:楕円の式は双曲線の式とよく似ているのでお互いに間違えないように注意しましょう。
楕円の定義と導出
楕円の定義は、この3つの中では最も単純かもしれません。
焦点2つ(FとF'とします)があった時、点Fからの距離ともう一方の焦点F’からの距離の和が一定である点(これを点Pとします)の軌跡が楕円になります。
楕円の式の導出
では、このPの軌跡を導出することで楕円の式を導いてみましょう。
楕円の式の導出の手順・計算は、双曲線の方程式を導く時とかなり似ています。
(互いの方程式自体も※で述べた様に似ているので、当然ですが・・・)
双曲線と違う点は【一定の“差”なのか、一定の“和”なのか】の一点だけです。
従って、まず”一定の距離”を2aとし、焦点FとF‘の座標を(f,0),(-f,0)とします。
PFとPF'の和が常に2aなので、Pを(x,y)とおくと次の式が成り立ちます。
PF+PF'=2a
(今回の楕円の場合は、『距離+距離=正+正>0』なので、絶対値は必要ありません。)
\(\sqrt{(x-f)^{2}+y^{2}}+\sqrt{(x+f)^{2}+y^{2}}=2a\)
移項して、\(\sqrt{(x-f)^{2}+y^{2}}= 2a-\sqrt{(x+f)^{2}+y^{2}}\)
ルートを外すために2乗し、
\(左辺の二乗=(x-f)^{2}+y^{2}\)
\(右辺の二乗= 4a^{2}-4a\sqrt{(x+f)^{2}+y^{2}}+(x+f)^{2}+y^{2}\)
さらに変形していきます。(詳しくは→:「双曲線の方程式の導出」を参照してください)
\(x^{2}(a^{2}-f^{2})+a^{2}y^{2}=a^{2}(a^{2}-f^{2})\)
ここで、この式の両辺を\(a^{2}(a^{2}-f^{2})\)で割ることで
$$\frac {x^{2}}{a^{2}}+\frac {y^{2}}{(a^{2}-f^{2})}=1$$
が導けました。あとは、双曲線の式の場合と同様に、"a2-f2=b2 "とおくことで、次の項で紹介している式が求まります。
楕円のグラフと焦点・長軸/短軸
楕円の一般式は次のように表されます。$$\frac {x^{2}}{a^{2}}+\frac {y^{2}}{b^{2}}=1$$
この時、焦点の座標はそれぞれ\(F(\sqrt{a^{2}-b^{2}},0)\)、\(F'(-\sqrt{a^{2}-b^{2}},0)\)ただしa>b。
もしくは、b>aの時、\(F(0,\sqrt{a^{2}-b^{2}})\)、\(F'(0,-\sqrt{b^{2}-a^{2}})\)となります。
また、円の半径に当たる部分がない代わりに
・”長軸”
と
・”短軸”
・(a>bの時:下図のようにaから-aが長軸で2a、bから-bが短軸となって2b)、
・(b>aの時、bから-bが長軸で2b、aから-aが短軸で2a)が存在します。
ちなみに、a=bの時がこれまで学んできた『円』です。
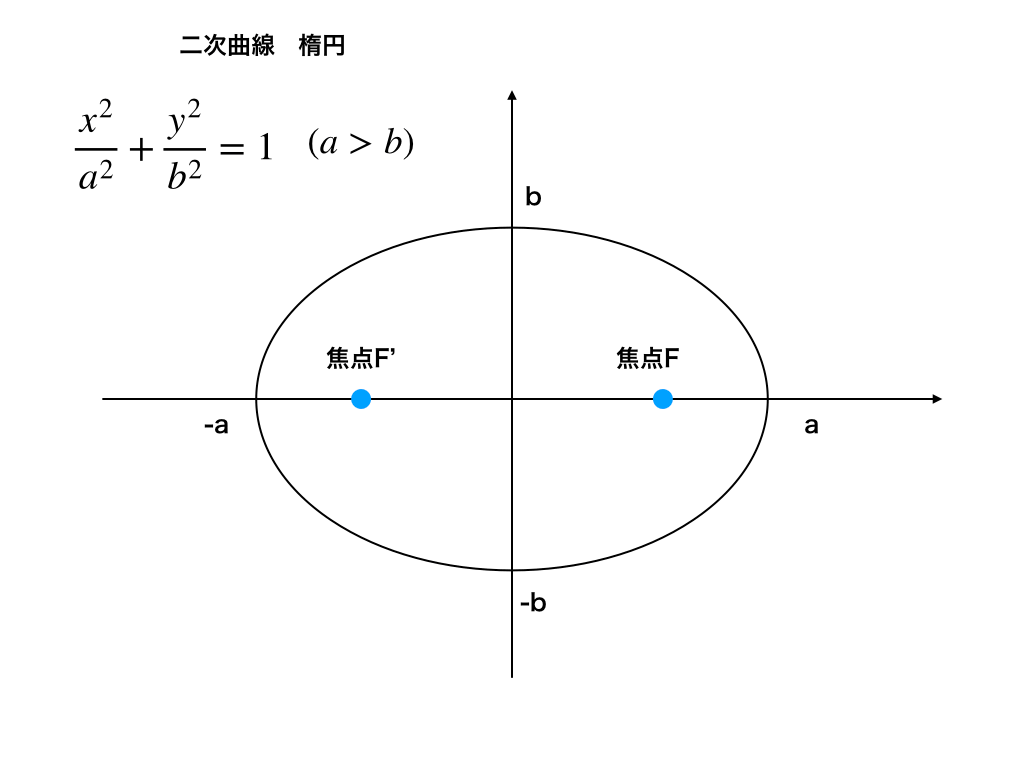
<楕円(a>b)のグラフ>

<楕円(b>a)のグラフ>
楕円の面積公式や接線の求め方
ここでは、楕円の面積と接線の式の求め方をそれぞれ紹介していきます。
楕円の面積公式
円の面積公式はπr ^2でしたが、楕円の場合にはr(半径)が求められないので、次の公式で面積を求めます。
S=πab: 円周率×(半長軸×半短軸)
これは、円の場合も当然成り立ちます→(円は長軸=短軸:a=b=r)なのでS=πr2
楕円の接線
今度は接線の方程式の求め方です。『数学2:図形と方程式』で円の接線は次のように習ったはずです。
\(x^{2}+y^{2}=r^{2}\)の時、\(点P(x_{0},y_{0})\)で接する接線の方程式は、\(xx_{0}+yy_{0}=r^{2}\)
楕円の場合も、”x、yの二乗の部分”を(接点のx座標)・(x)と(接点のy座標)・(y)とすることに変わりはなく、
$$\frac {x_{0} x}{a^{2}}+\frac {y_{0}y}{b^{2}}=1$$が接線の式となります。
楕円のまとめと二次曲線シリーズ
・楕円は双曲線の「焦点からの『差』が一定」の定義を「焦点からの『和』が一定」に変化させたもの。
・長軸=短軸、すなわち2つの焦点が同じになった時『円』となる
・上記の理由から、双曲線の式と楕円の式の導出はよく似ているので、要注意!
・次回は、二次曲線の応用に入っていきます。
二次曲線シリーズと関連記事一覧
第1回:「二次曲線と円錐の関係・そして放物線」
第2回:「双曲線の式の導き方とそのグラフ」
第3回:「楕円の式・グラフと面積(今ここです)」
第4回:「(現在作成中です)二次曲線の離心率・応用問題の解法など・・・」
発展:「二次形式とその標準形(大学レベル)」
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
ご質問・ご意見がございましたら、是非コメント欄にお寄せください。
B!やシェア、Twitterのフォローをしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

