円運動と遠心力+応用問題
<この記事の内容>:円運動と向心力・遠心力を基本的なレベルから紹介(・復習)し、頻出問題である「バネとの融合」や「ジェットコースター」の問題を通して応用力をつけていきます。
<関連記事>:「“等速”円運動と単振動(その一)」
目次(タップした所へ飛びます)
円運動の基礎(復習)と確認問題
円運動の諸公式
常に円の中心に向かって生じる力(これが無いと、《円運動をしている》円の接線の方向に飛び出してしまいます):$$向心力F=m\frac{v^{2}}{r}=mr\omega^{2}$$
上の向心力を、同時に回転しているもの(人)から見ると、円の中心の反対方向へ\(F=m\frac{v^{2}}{r}=mr\omega^{2}\)の大きさの「遠心力」によって物体が静止している様に見えます。
これは、慣性の法則のところで学んだ、慣性力と同様なので場合によって使い分けます。
\(T=\frac{2\pi}{\omega}=\frac{2\pi r}{v}\)
バネと遠心力の融合問題
では基本問題を使って円運動ではどの様なことが問われ、どうやって解いていくのかを紹介します。
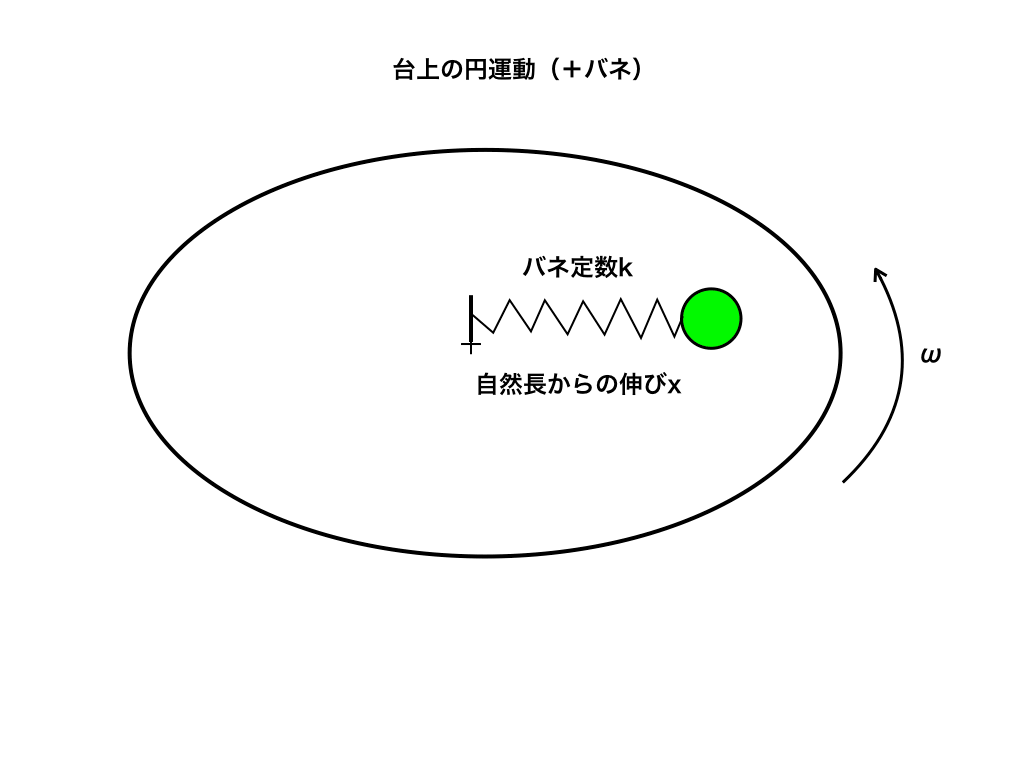
問1:いま、<図1>のような円盤が有り、この円盤の中心にバネ定数”k”、自然長"l"のバネを取り付け、もう一方には質量mの球を取り付けた。
次に円盤を回転させて、角速度が\(\omega\)になるとバネは自然長よりもxだけ伸び、球は等速円運動をした。
(1):この時のバネの伸びを求めよ。
解説(其の一)
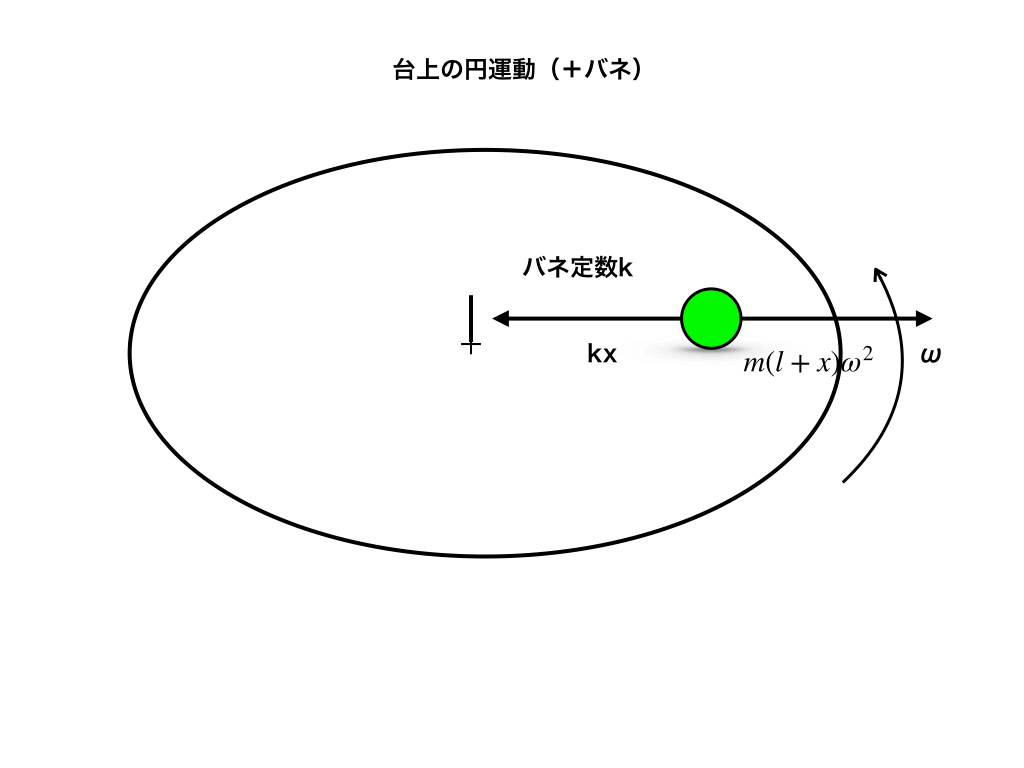
とりあえず(円盤上から見た)小球にかかる力を書き込んでいきます。水平方向のみ書き出すと、以下の<図2>の様に\(kx=m(l+x)\omega^{2}\)。
バネの伸びをxとすると、上の式を変形して(xが左右二箇所にあるので注意)
$$x=\frac{lm\omega^{2}}{kーm\omega^{2}}$$
<解説図2>
(円盤の外から見て、運動方程式を立てることでも同じ答えを得ることが出来ます。)
遠心力と円運動の応用
さて、ここからは応用問題を解いていきます。いろいろなエッセンスが詰まった問題で、類題は頻繁に出題されているのでしっかりと理解して、確実に解ける様にしておきましょう!
ジェットコースターの問題(落下しない条件)
応用問題2:いま、以下の<図3>のように質量2mの”小球”が高さ3hの点Aにある。BC間は半円になっておりその半径をrとする。
点Aから点A'、点A'から点B、点Bから点Cまでは滑らかにつながっており、摩擦力が働かないものとする。
このとき以下の(1)、(2)、(3)に答えよ。(重力加速度はgとする)
(※:ジェットコースターを”小球”に見立てています)
(1):Bにおける球の速度\(V_{B}\)とBを通過する直前に球が水平面から受ける力(=垂直抗力)を求めよ。
(2):Bを通過した直後に球が水平面から受ける垂直抗力を求めよ。(このとき\(V_{B}\)を使用して良い)
(3):点Cまで小球が曲面BCを離れることなく達した。この時、点Cで小球が落下しない『r』の条件を示せ。

<応用問題2:図3>
解答・解説
力学的エネルギー保存則、力のつりあい、円運動(遠心力)などが組み合わさった問題です。
さっそく(1)、(2)から見ていきます。
垂直抗力Nの意味
(1):まずは\(V_{B}\)について。摩擦がないので、《Aでの位置エネルギー》が全て《Bでの運動エネルギー》に変換されます。
したがって、力学的エネルギー保存則より\(2mg\cdot 3h=2mg\cdot 0+\frac{1}{2}2m\cdot V_{B}^{2}\)
故に、\(V_{B}=\sqrt{6gh}\)
次にBを通過する【直前】の垂直抗力\(N_{B前}\)を求めます。
(※重要ポイント!):「直前」と「直後」では全く異なります。「直後」では、円運動に入るために遠心力を考慮する必要があるからです。
対して、「直前」では、単に重力と垂直抗力という二つの鉛直方向の力のみを考えれば良いので、
\(N_{B前}=2mg\)が(答)です。
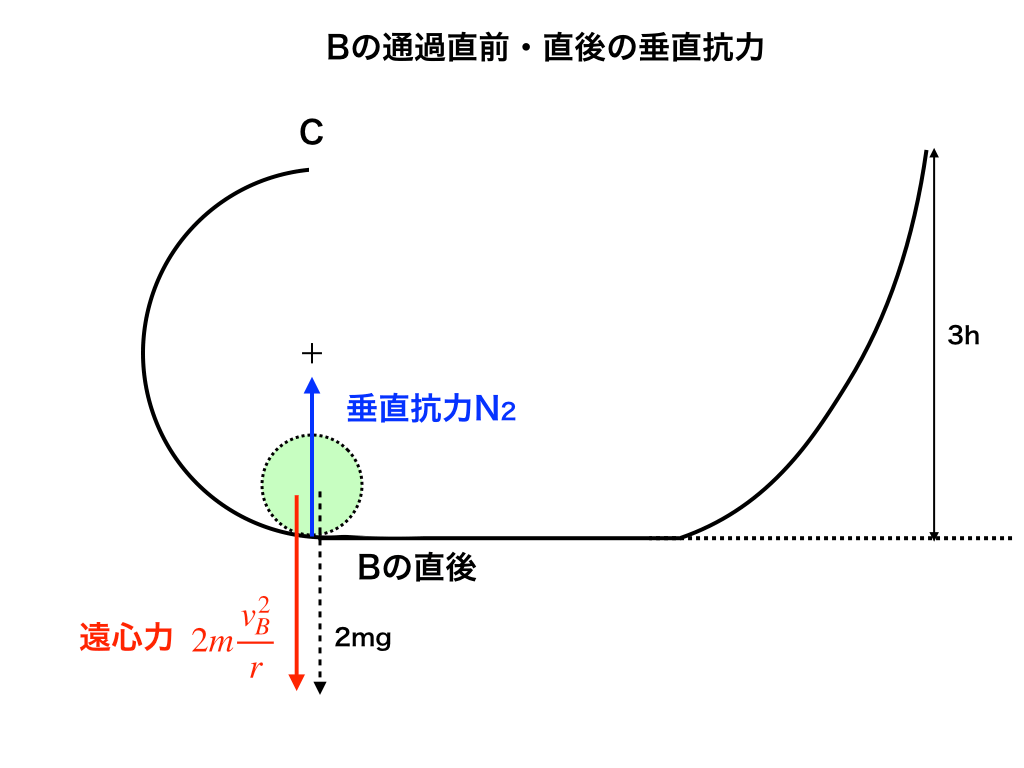
(2):上述した通り、\(N_{2}\)では遠心力を考えます。すると、以下の<図4>の様に力の矢印を書き込んで、$$N_{2}=2mg+2m\frac{V_{B}^{2}}{r}$$
<解説図4>
落下しない条件と力の図示
(3)では、Cで小球が落ちない条件を問われています。以下の<図5>のように、球にかかる力は
・鉛直下向きに
・垂直抗力\(N_{2},重力 2mg、\)
・鉛直上向きに
・遠心力\( 2m\frac{V_{C}^{2}}{r}\)
とすることが出来ます。
ここで最重要:【落下しない=垂直抗力が0以上】を用います。なぜなら、「垂直抗力Nが負」と言うことは「球がCから力を受けていない」=「接触していない」=「離れている」からです。
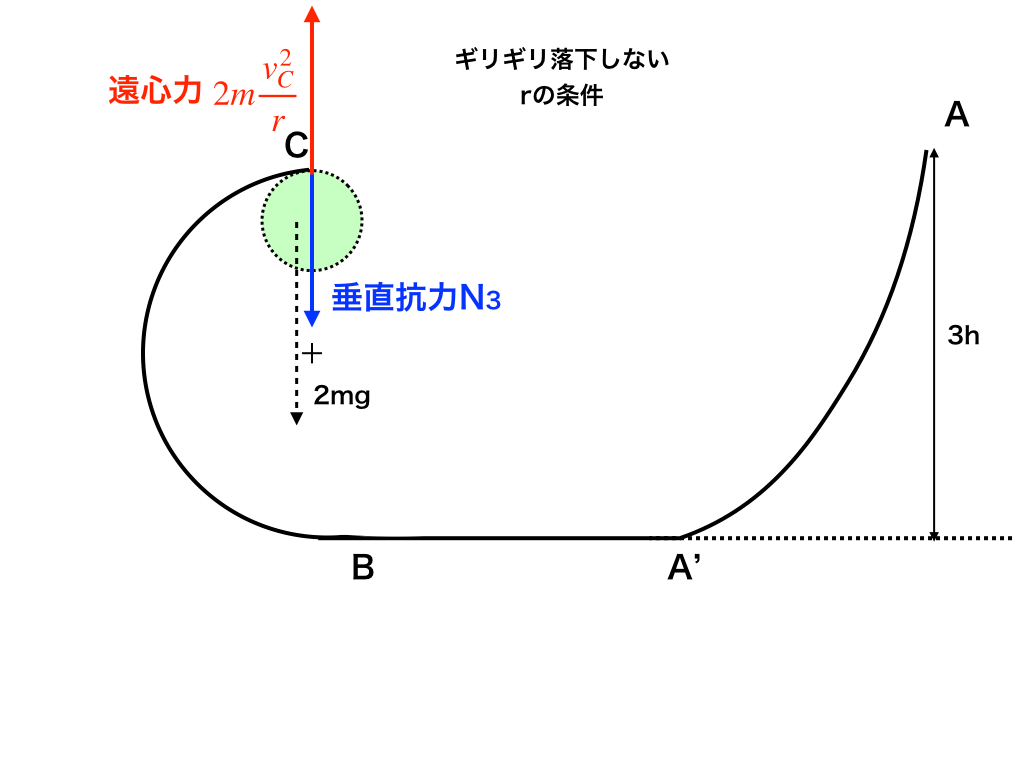
<解説図5>
後は、鉛直方向の力を立式して
$$ 2m\frac{V_{C}^{2}}{r}=N_{3}+2mg$$
で\(N_{3}=0\)
\(2m\frac{V_{C}^{2}}{r}-2mg=0\)
ここで\(V_{C}\)が必要なので、エネルギー保存則より、$$ 2mg\cdot 3h=2mg\cdot 2r+\frac{2m}{2}V_{C}^{2}$$
計算して整理すると\(\frac{6h}{r}=5\)
故に、\(r=\frac{6}{5}h\)(答)
円運動まとめ
この様に、向心力(あるいは遠心力)を用いて運動方程式・力の釣り合いの式を正確に書くことに慣れれば、次の項で紹介している「単振動」や「宇宙スケールの問題」もそれほど苦労せず解くことができる様になります。
ぜひ続けて以下の記事もご覧下さい!
円運動・単振動・万有引力の関連記事へ
単振動へ進みたい方は
>>「単振動(一)微積“使用・不使用”の両方で丁寧に解説!」
“万有引力”/”ケプラーの法則“との融合問題は
>>「第一宇宙速度とは?」
>>「“第二”宇宙速度と“万有引力の【位置エネルギー】”がマイナスな理由をイラストで説明!」
>>「ケプラーの3法則を解説!」
最後までご覧いただきまして、有難うございました。
「受験・学習メディア:『スマホで学ぶサイト、スマナビング!』」では,読者の皆さんのご意見・ご感想を募集しています。ぜひコメント欄までお寄せください。
(※:現在、個々の問題や,証明の質問等には対応出来ない場合がございます。)
・その他のご依頼、タイアップ等に付きましては、【運営元ページ】よりご連絡下さい

