
単振動(2)と摩擦力
今回は前回に引き続き「摩擦力の働く単振動」を扱います。
未読の方はこちら↓を先にお読み下さい
目次
(1)単振動の問題の解き方/順序のおさらい
(2)摩擦力が働く物体の単振動
(3:new!)単振り子の記事&「浮力と単振動の融合問題」を作成しました
目次(タップした所へ飛びます)
単振動の問題の解き方のおさらい
前回同様に問題の解き方の順序を載せておきます。
step1:軸(正の向き、原点)を決める
step2:物体にかかる全ての力を書き出す
step3:運動方程式ma=Fを立てて、a=ー◯xの形に変形する。
step4:周期T、振動中心X0、振幅Aを求める
摩擦力が働く物体の単振動
今回は、摩擦力を扱うので、→「摩擦力とは?”動”摩擦力/”静止”摩擦力の違いや計算方法まとめ」←を読んでいない方はぜひ先にご覧下さい!
(例題2):今<図1>の様に質量mの物体Aが動摩擦係数μ‘の床に接して置かれている。又、
Aは壁とバネ定数k、自然長L0のバネでつながっている。物体Aを右向きにαだけ引っ張った時、
物体Aは左向きに動き始めた。この時の単振動の周期と振幅、振動中心を求めよ。但し重力加速度をgとする。
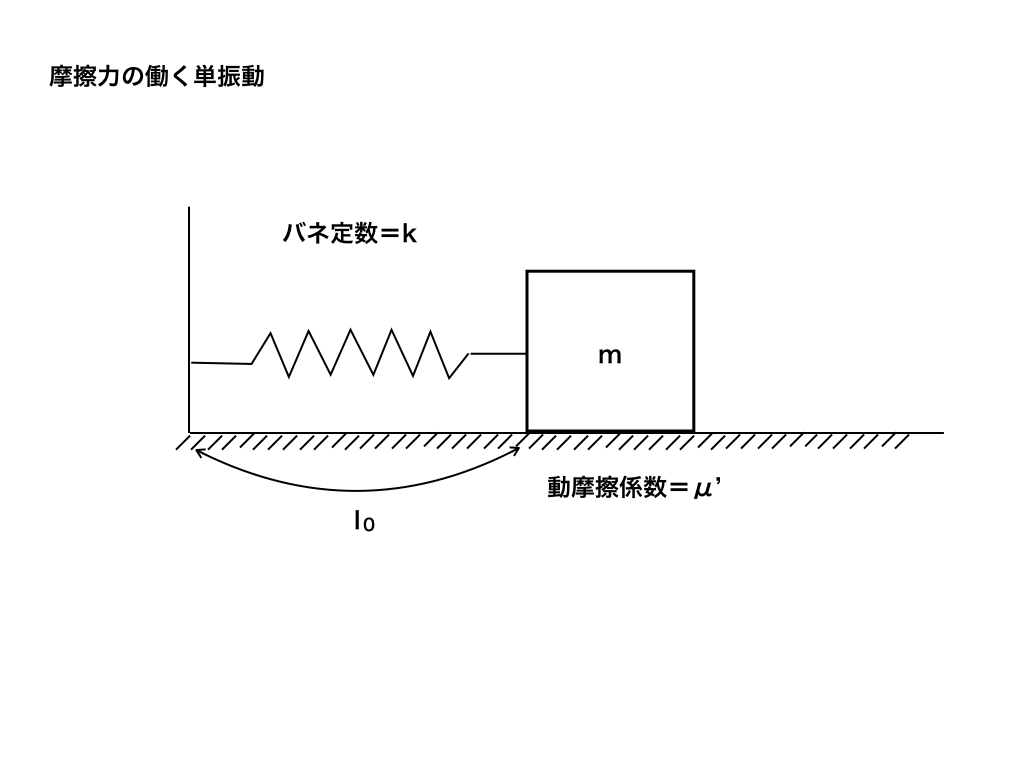
<図1>
前回の例題に摩擦が加わった分レベルが少しだけアップしていますが、解く手順は同じです。
上記のstepを順番にこなしていくだけです。
step1:軸の設定
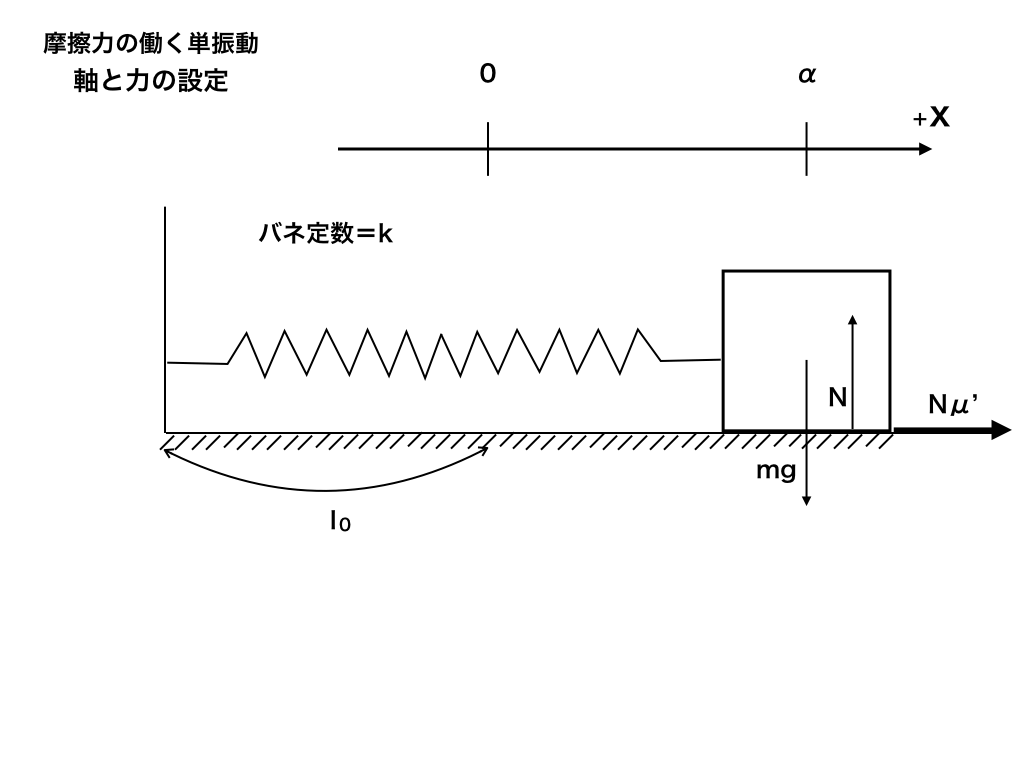
<図2>
ここでは<図2>の様に右向き正で原点を壁からL0の位置に設定します。
step2:物体に働く全ての力を書き出す
この問題では、水平方向だけでなく鉛直方向も重要になってきます。(動摩擦力=動摩擦係数μ'×垂直抗力N)
まず水平方向:負の方向にkx(バネの弾性力)、正方向に摩擦力μ‘N
鉛直方向:下向きにmg、床からの垂直抗力N
step3:運動方程式ma=Fを立てて、a=ー◯xの形に変形する。
step2冒頭で書いた様に、今回は摩擦力μ’NのNが必要なので、鉛直方向の力も利用する必要があります。
鉛直方向の力は釣り合っているので、
N=mg
水平方向の運動方程式にN=mgを代入して、ma=−kx+μ‘mg
$$ma=-kx+\mu 'mg$$
ここで上の運動方程式をa=ー◯xの形に変形すると、
a=−kx/m+μ’g ⇔a=−k/m(xーmμ‘g/k)
$$a=\frac {-k}{m}x+\mu 'g$$
$$a=-\frac {k}{m}\left( x-\frac {m}{k}\mu 'g\right) $$
step4:周期T、振幅A、振動中心X0を求める
a=ーω^2x と比べて、ω^2=k/m
ω=√k/m、T=2π/ω
∴ T=2π√m/k
$$T=2\pi \sqrt {\frac {m}{k}}$$
振動中心は、加速度がゼロになる場所(速度は最大)なので、
a=−k/m(xーmμ‘g/k)より、a=0の時,0=−k/m(xーmμ‘g/k)、
$$0=-\frac {k}{m}\left( x-\frac {m}{k}\mu 'g\right)$$
この式を満たすxは、
$$x=\frac {m}{k}\mu 'g$$
x=mμ‘g/k
∴ 振動中心$$x_{0}=\frac {m}{k}\mu 'g$$
振幅は(初めの位置ー振動中心)で、
∴$$\alpha -\frac {m\mu 'g}{k}$$
振幅:αーmμ‘g/k
これで3つ答えが揃いました。
減衰振動と力学的エネルギー
(2 ーα)今回の問題の更に応用として、「単振動が起こる条件」や、「この後物体がどの様に運動していくか」を問われることがあります。
少し考えてみてください。
・・・・・・・
・・・・・・・
<答え合わせ>
単振動が起こる条件:静止摩擦係数μ0と、はじめに引っ張る距離αによるバネの弾性力を使って
kα>μ0N=μ0mg つまりバネの復元力が静止摩擦力より大きい時に単振動が起こる。
今後の物体Aの運動:これはαの大きさによって違うのですが、摩擦がある場合は摩擦がない場合と違って、段々と振幅が小さくなり最終的には停止します。
(力学的エネルギーが保存されず、摩擦によって熱エネルギーなどに変化するため)
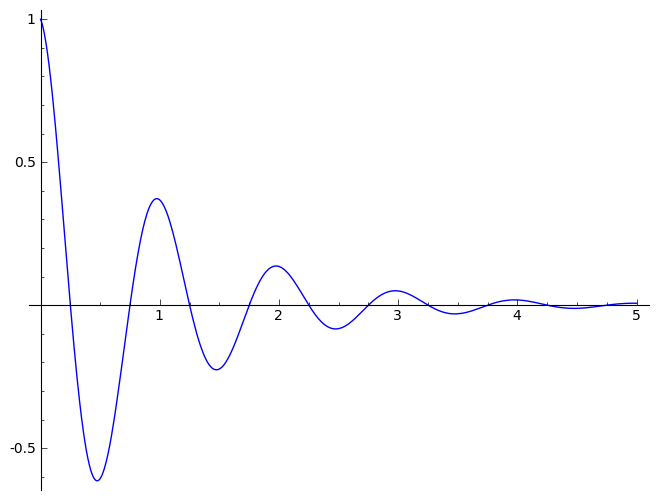
image by Lm13700
これを減衰振動と言い、入試でもグラフなどの形で問われることがあるので、頭に入れて置いて下さい。
今日もお疲れ様でした!
単振り子について:近似と運動方程式から周期を導出する方法
続編として、単振り子の記事を作成しました!続き→「単振り子の考え方と周期の導出」を読む。
2018/10/27(NEW):「浮力とは?そして単振動との融合問題」を読む。
記事リクエスト、質問、お問い合わせ、その他はコメント欄にお願いします。
お役に立ちましたら、シェアお願いします!

