静止摩擦力(最大静止摩擦力)と動摩擦力
今回は、高校物理(力学)から「動摩擦力・静止摩擦力・最大静止摩擦力」の解説を中心として、「力学的エネルギー保存則」との関係を融合問題を通して紹介していきます。
目次(タップした所へ飛びます)
摩擦力とは?3種類の意味と使い分け
摩擦力(まさつー)は非常にありふれた力なので、物理や理科の勉強をする前から知っていたのではないでしょうか。
この記事では、その摩擦力を高校物理のレベルで3種類に分類していきます。
以下の説明は、<図1>の様な状況の時を例にしています。
さらに、静止摩擦係数をμ(ミュー)、動摩擦係数をμ'とします。
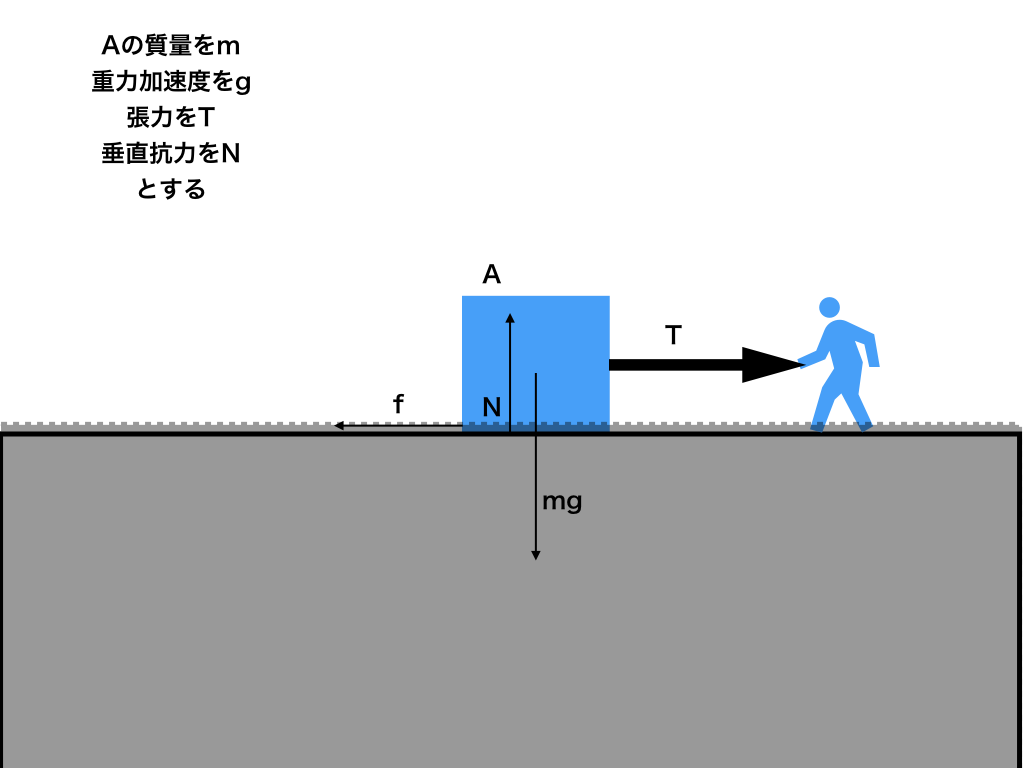
<図1:粗い表面上で質量mの物体を引っ張る>
静止摩擦係数μと静止摩擦力
摩擦力には二種類あり(最大静止摩擦力を入れると3種類)、これから解説する「静止摩擦力」と次の項で解説する「動摩擦力」があります。
「静止摩擦力」とは、文字通り静止=動いていない(止まっている)物体を動かそうとするときに、反対方向に働いて「すべり出すのを妨げる」力です。
(一)注意が必要なことは、あとで紹介する「動摩擦力」と違って静止摩擦力は一定ではない、という点です。
(二)もう一つのポイントは、「静止摩擦力≠μN=μmg」だと言うことです。
最大静止摩擦力とグラフ
特に二番目の「静止摩擦力≠μN=μmg」は、多くの人が式を立てるときにやりがちな間違いなので気をつけてください。
静止摩擦力は、あくまで静止している物体を動かそうとする力と同じ値です。
つまり、強い力で引っ張れば静止摩擦力は大きくなり、弱い力で引っ張れば静止摩擦力は小さくなります。
では何故この様な勘違いが起こるかというと、「最大静止摩擦力」と言うのものの存在が原因です。
先ほど説明した「μmg」は「最大静止摩擦力」、
つまり物体が動き始める【ギリギリ】の状態の時に成り立つ値なのです。
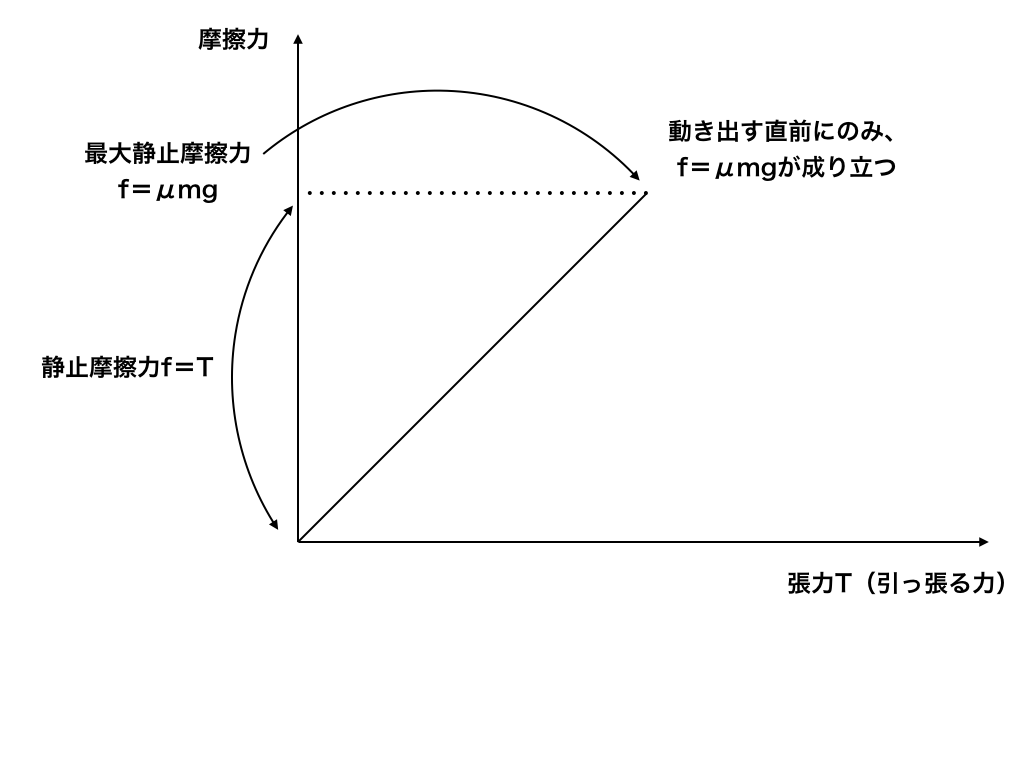
<図2:静止摩擦力ー張力のグラフ>
<図2>の【摩擦力fー張力T】のグラフを見てください。
動き始めるギリギリまで、静止摩擦力”f”は引っ張る力につれて大きくなって行きます。
この時はまだμmgではありません。
そして、やっと動き始める直前に静止摩擦力fは最大静止摩擦力f0となり、その力の大きさf0=μmgとなります。
つまり、
・静止摩擦力は一定ではない
・静止摩擦力はf=μmgではない
・μmgになるのは動き始めるギリギリの時で、その時の摩擦力を「最大静止摩擦力」とよぶ。
とまとめることができます。
動摩擦係数μ‘と動摩擦力
次に、物体Aが動き始めた後の摩擦力、すなわち「動摩擦力」について解説して行きます。
動摩擦力は静止摩擦力に比べると比較的単純で、「動摩擦係数μ'」×「垂直抗力N」で求められます。
<図1>の状況で、物体Aが右向きに動いている(運動している)とすると、
・(垂直方向の力の釣り合いの式):N=mg
・(水平方向の運動方程式):ma=T-μ'N
が立式出来ます。
そして、水平方向のつり合いの式を運動方程式に代入すると、
ma=T-μ'mg となり、等加速度運動をしていることがわかります。
静止摩擦力と動摩擦力の違いとグラフ
では、最大静止摩擦力と動摩擦力はどの様な違いがあるのかグラフで見て見ましょう<図3>
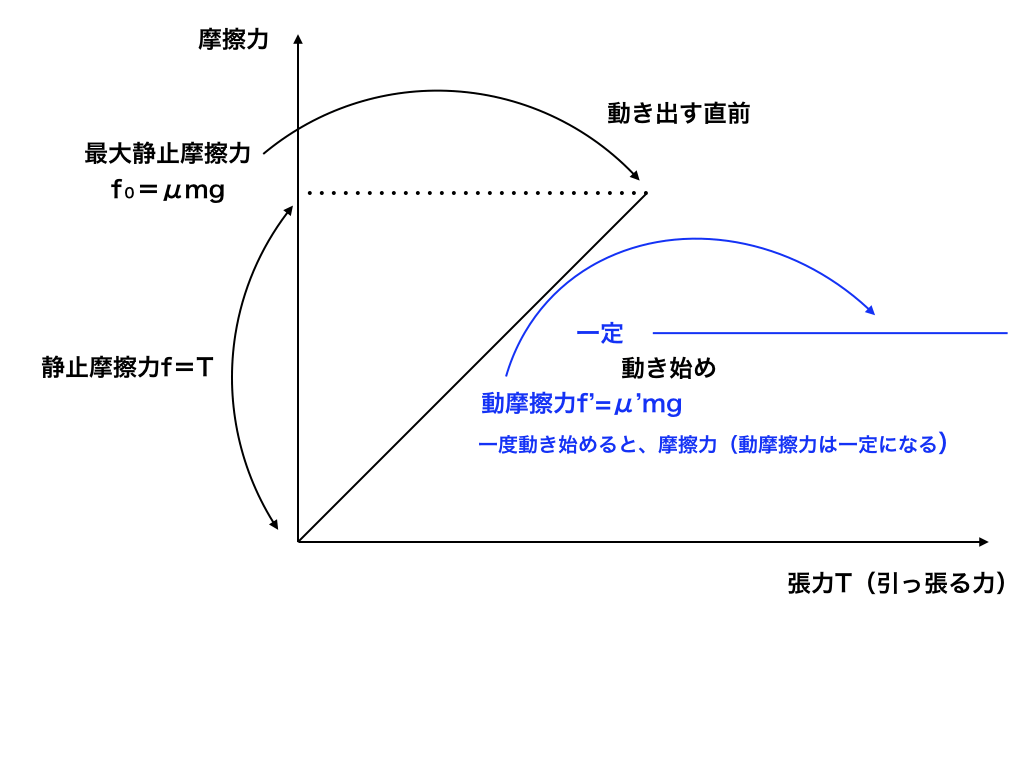
<図3:静止摩擦力、動摩擦力ー張力Tのグラフ>
動摩擦力は一般的に最大静止摩擦力よりも小さく、一定の値をとります。
この現象は、よく「ものを引っ張った時、動き出すまでは大変だが、一度動き始めると比較的弱い力で動かせる」と言う風に表現されます。
実際にこの現象を経験した人も多いかと思います。
摩擦力のする仕事と力学的エネルギー保存則
ではここからは、仕事とエネルギーについてのお話に入っていきます。
エネルギー・仕事の復習と種類
「仕事(量)」は、「力」×「距離」で表すことができ、
エネルギーはその仕事をするために持っている「能力」のようなものです。
エネルギーには、運動エネルギーや位置エネルギー、弾性エネルギー、光エネルギー等々いろいろな物がありますが、
一般的に高校物理では「力学的エネルギー」として「運動エネルギー」「位置エネルギー」「バネによる弾性エネルギー」を扱います。
力学的エネルギーは外部から仕事をされたり、したりしない限りは一定で保存します。(力学的エネルギー保存則)
>力学的エネルギー保存則の導き方については→「力学的エネルギー保存則と運動量保存則を運動方程式から導く」←で解説しています。余裕があればご覧ください。
では、摩擦がある様な場所ではどうなるのでしょうか?下の例題を通して見ていきます。<図4>
摩擦力と力学的エネルギー保存則の例題
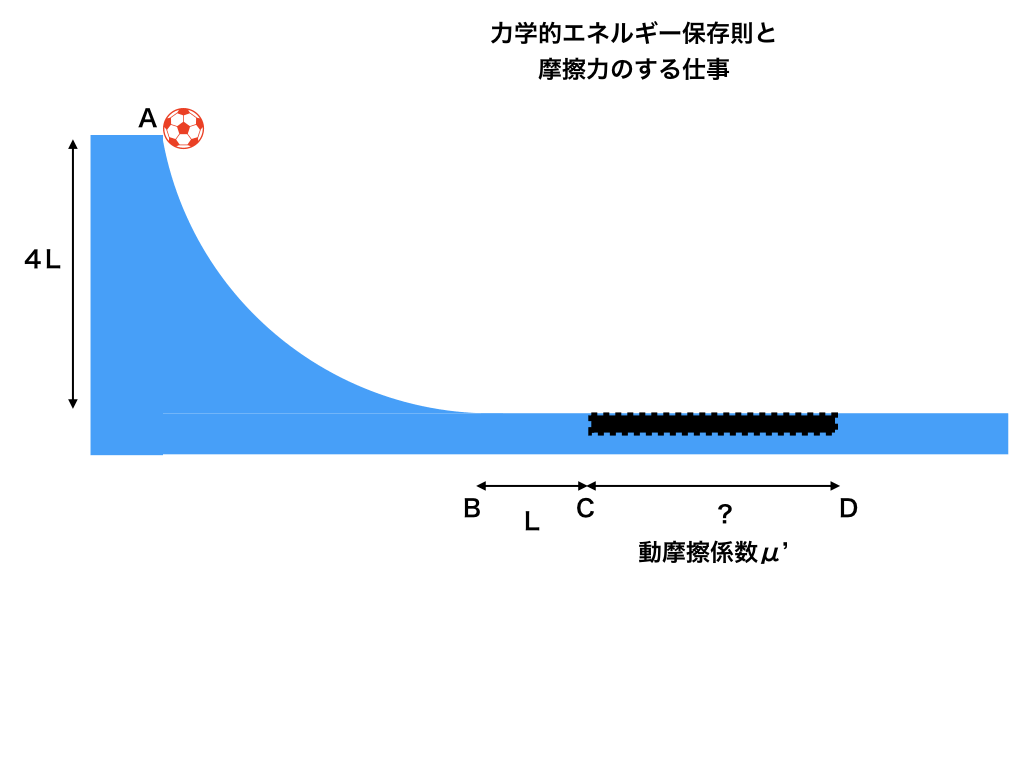
<図4:力学的エネルギー保存則と動摩擦力がする負の仕事>
問題1:<図4>の様に青色の動かない台上の点Aに質量mの球を置く。
AB間はなめらかな曲線であり、この曲線上を球が離れずすべり降りたとき、点Bでの速度VBはいくらになるか。
但し、高さはB,C,Dのある台上を基準とし、重力加速度をgとする。
問題2:BC間も同様になめらかな直線だったが、点CからDまでは動摩擦係数がμ'の粗い直線であった。
ちょうど球が点Dで止まったとき、点CD間の距離LCDはいくらであったか。
L、m、g、μ’を用いて答えよ。
解説編
基本的な問題から固めていきます。
解答1:この問一は、位置エネルギーを運動エネルギーに変換するだけの問題です。
点Aで球は位置エネルギーmg4Lを持っています。
それが基準点=高さ0まですべり下りるとmg0L=0になります。
この変化の途中では仕事をされたり、したりしていないので、
位置エネルギーmg4Lは全て運動エネルギーに変換されます。
$$よって、mg4L=m\frac{{V_{B}}^{2}}{2} の式$$
が成立するので、8gL=VB2
$$V_{B}=2\sqrt{2gL}$$
解答2:BC間はなめらかなので
→(物理で「なめらか」と書いてあれば「摩擦が無い」、
→「粗い」と書いてあれば「摩擦がある」という意味で使われることがほとんどです。)
、速度は変化しません。
点CからDの間は粗い=動摩擦係数μ‘の表面であるので、摩擦があります。
摩擦力は、球の持っている力学的エネルギーを熱や光エネルギーに変えてしまい、最終的に運動エネルギーがゼロになると球は止まります。
今問2ではCD間の距離を問われているので、CD間の距離をLCDとおくと、
仕事=力× 距離 より、
\(mgμ’ × L_{CD}が、\)
\(mg4L=m\frac{{V_{B}}^{2}}{2} と等しくなる\)
時の\(L_{CD}\)を求めれば良いので,\(4mgL=μ’mgL_{CD}\)
\(⇔ 4L=μ‘L_{CD}\)
$$⇔ L_{CD}=\frac{4L}{μ’}$$
が答えになります。
摩擦力のまとめ
・静止摩擦力を扱う時は、「最大」静止摩擦なのか要チェック
・動摩擦力は最大静止摩擦力より小さく、一定
・力学的エネルギー保存則と仕事、摩擦力に関する問題は頻出なので、類題を見つけて復習する
・余裕があれば、「運動方程式の解と力学的エネルギー保存則の導出」を読んでみる。
力学の記事まとめへ
次回は、力学的エネルギー保存則と運動量保存則の二式を扱う問題を解説する予定です。

