力のモーメントと摩擦力の攻略
<この記事の内容>:苦手な人がかなり多く、スルーされがちな『力のモーメント』について図を用いながら頻出問題を解く方法を通して解説しています。
<関連する記事>:「よくある疑問:摩擦力3種類について解説!」
目次(タップした所へ飛びます)
力のモーメントとは
力のモーメントとは「回転させるチカラ」ということができ、他の多くの高校物理の力学の問題(質点の運動についての問題)では考慮しない『物体自体の回転運動』の問題を解く際になくてはならないものです。
質点と剛体/回転運動と並進運動
質点とは:「大きさを無視する」物体
→《並進運動》のみ
剛体とは:「大きさがある」物体
→《並進運動》だけでなく【回転運動】も行う
(※:【回転運動】と《並進運動》というものが存在し、普段解いている「質点の運動」は《並進運動》と呼ばれています。)
回転させる力の定義と単位
力のモーメントは、軸から(作用線へ垂直に下ろしたキョリ)掛ける(力)→\(単位:N(Nm)=F\cdot l\)で計算します。詳しくは例題2・3にて。
正確には高校範囲外の「外積(ベクトルのもう一つの掛け算)」を用いて説明されますが、高校・大学受験までは上記の考え方でokです。
合力の図示と計算の仕方
ここでは剛体にかかる力の向きと大きさ、その合力について見ていきます。
パターン1:長さが5l(m)ある剛体の右端と左端に、それぞれ200(N)、50(N)の力が下向き(同方向)にかかっている。
このときの合力の(作用点の)位置と大きさを求めよ。
パターン2:長さl(m)の剛体の右端と左端に50(N)、100(N)の力が上向きと下向きの逆方向にかかるときの合力の(〃)位置と大きさを求めよ。
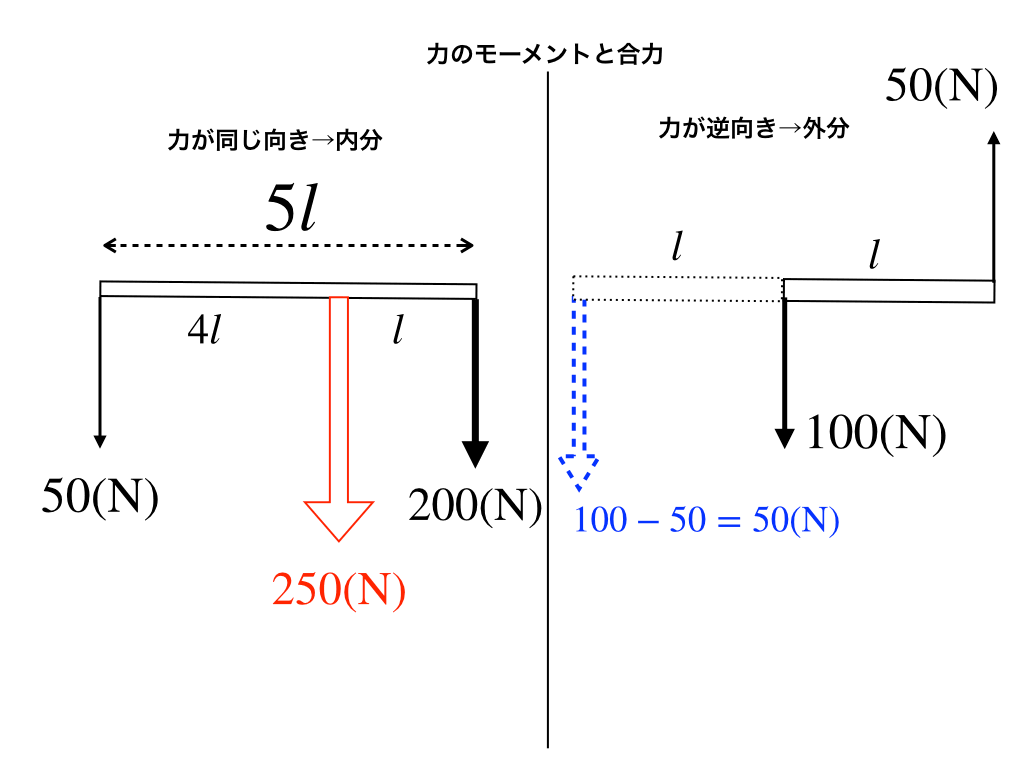
合力のパターン1(内分)
上図の左の様に同じ方向に力がかかるならば、その合力(の作用点)は【力の逆比に内分した点】に位置し、二つの力を【足し合わせた】ものになります。
∴合力の位置と大きさ:50:200=1:4の逆比の内分→左端から4lの位置に200+50=250(N)
合力のパターン2(外分)
上図の右の様に、逆方向に力がかかっているなら、その合力(〃)は力の逆比に【外分】した点に位置し、二つの力を【引いた】ものになります。
∴合力の位置と大きさ:50:100=1:2の逆比の外分→左端から「更にl」だけ左の位置に100-50=50(N)
モーメントに関する頻出問題
ここでは、力のモーメントを多用する『超頻出問題』を解きながら、この分野を攻略するコツや解法を学んでいきます。
立てかけたハシゴの例題2(剛体が動かない条件)
(例題2):以下の図のように、静止摩擦係数\(\mu\)の床から\(\theta\)傾けて壁に立てかけた\(長さl、質量M\)の剛体がある。
このはしごにかかっている力を描き、転倒しない条件を\(\thetaと\mu\)を用いて答えよ。ただし、重力加速度をgとする。
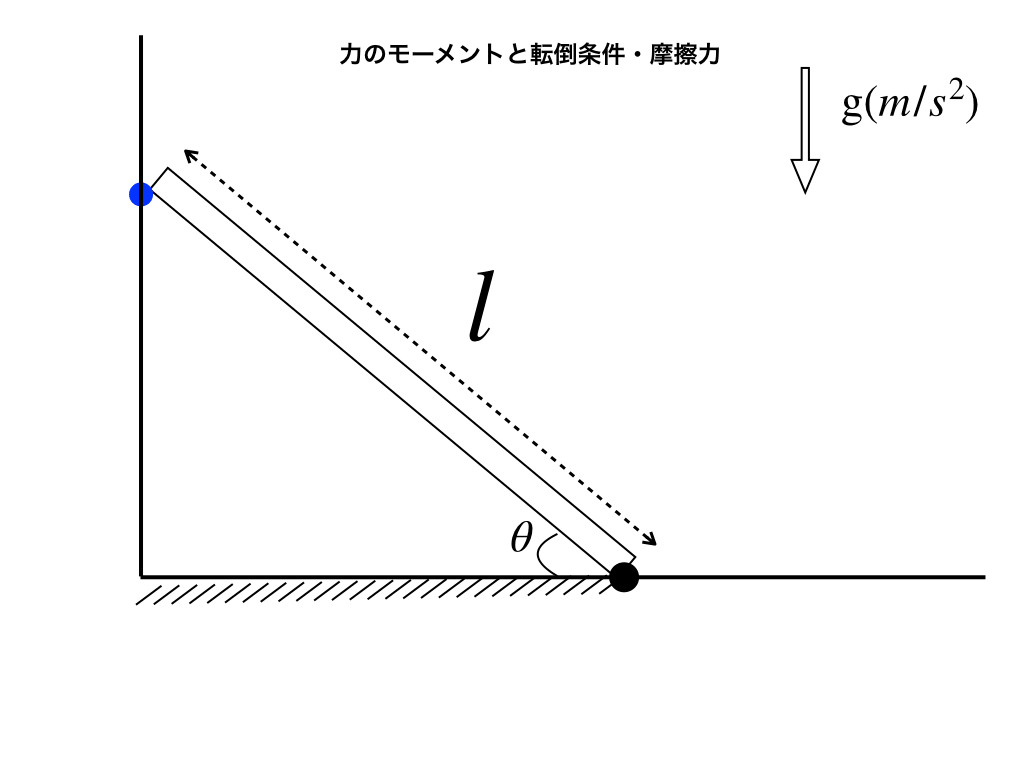
解説2:モーメントと力の両方が釣り合う
はじめに力を書き込んでいきます。
このような剛体が静止しているためのつりあいの式を作っていきます。
・水平方向の力の釣り合い
・鉛直方向の力の釣り合い
ここまでは、質点のときと同じ条件です。
・『時計回りのモーメント』と『反時計回りのモーメント』が釣り合っていること<<今回のpoint>>
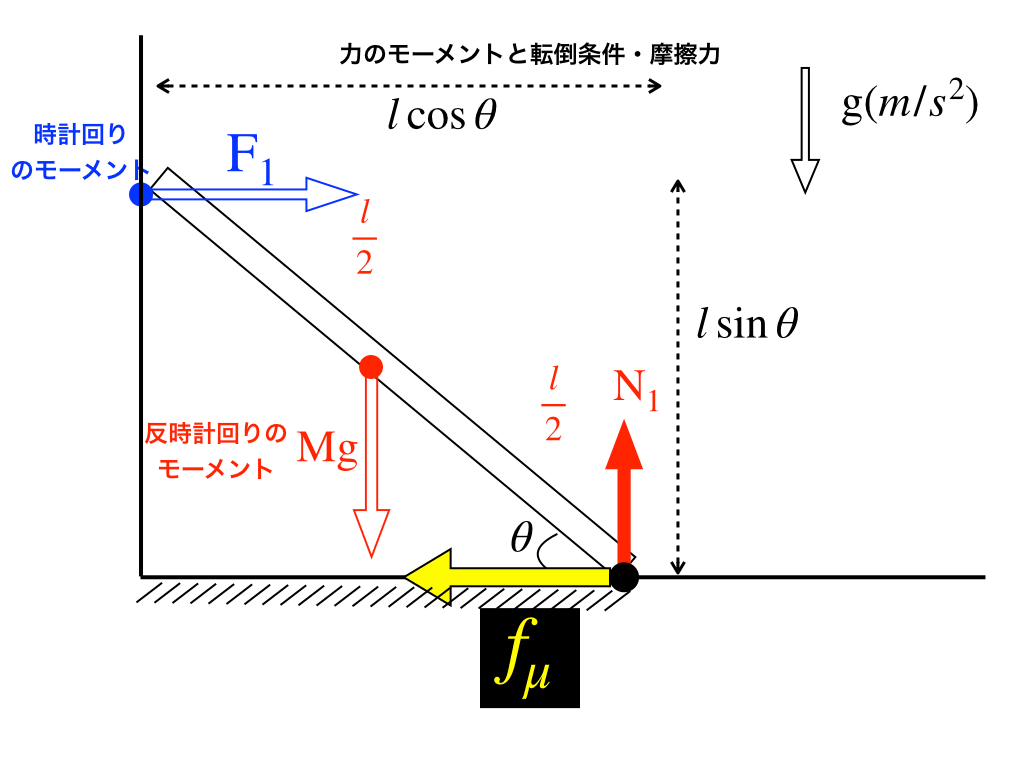
これらを考慮して力を描き込んだものが上の図です。黒丸の点を基準として、
・鉛直方向の力:\(N_{1}=Mg\)
・水平方向の力:\(F_{1}=f_{\mu}\)
さらに力のモーメントは、黒丸からの距離(ウデの長さ)・力なので
・$$\mathrm{Mg\cdot \frac{l}{2}\cos \theta=F_{1}\cdot l\sin\theta}$$
ここで\(F_{1}=f_{\mu}\)より、
・$$\mathrm{Mg\cdot \frac{l}{2}\cos \theta=f_{\mu}\cdot l\sin\theta}$$
よって、$$\mathrm{f_{\mu}=\frac{Mg\cos\theta}{2\sin\theta}}$$
\(f_{\mu}\)が最大静止摩擦力を超えると滑りだしてしまう事から、 条件は\(f_{\mu}≦Mg\mu\)
∴ $$\frac{Mg\cos\theta}{2\sin\theta}≦Mg\mu$$
上の式を整理して、$$\frac{1}{2\mu}≦\tan\theta$$
・・・(答え)
斜面上の直方体が先に倒れる条件(例題3)
(例題3):いま、図3のように摩擦の働く台上にたて\(\alpha、横\beta\)
(奥行きは考えないものとする)の直方体Xが置かれている。
Xの質量はmで、台を徐々に傾けていく。静止摩擦係数を\(\mu\)とし、下向きに重力加速度gがかかっている時次の問いに答えよ。
問1:Xが静止している時のXにかかっている力を図示せよ。
問2:黒丸に部分を支点とするXのモーメントを求めよ
問3:\(\theta\)をだんだん大きくしていったとき先にXが転倒しはじめる(すべらず先に傾く)条件を\(\muと\alpha,\beta\)で表せ。
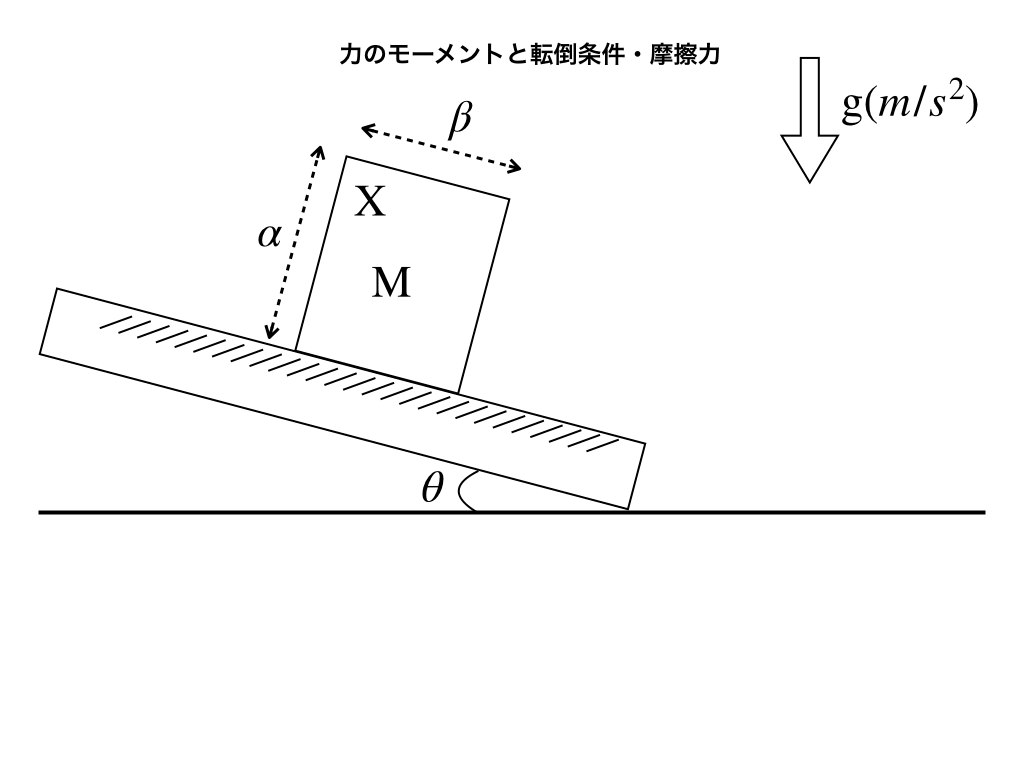
<問題図3>
解説3:力の図示
まずは、何と言っても力の図示です。
まずMgが鉛直下向きに、台から物体へ垂直抗力N、そして台の水平方向左向きに摩擦力fが働いています。
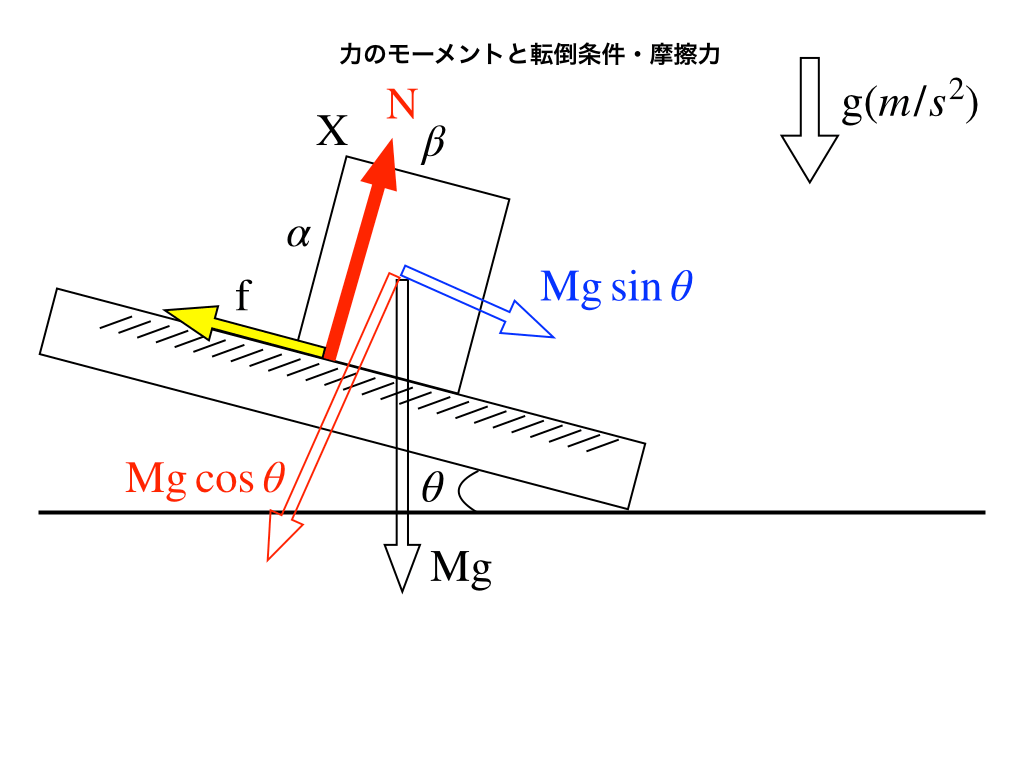
摩擦力vs時計回りのモーメント
では(2)・(3)の『転倒が先に起こる条件』を考えてみましょう。
平面と台のなす角をθとすると、Mgを台の垂直方向・水平方向にそれぞれ分解して、青矢印\(Mg\sin\theta \)と赤矢印\(Mg\cos\theta\)に分けて考えます。
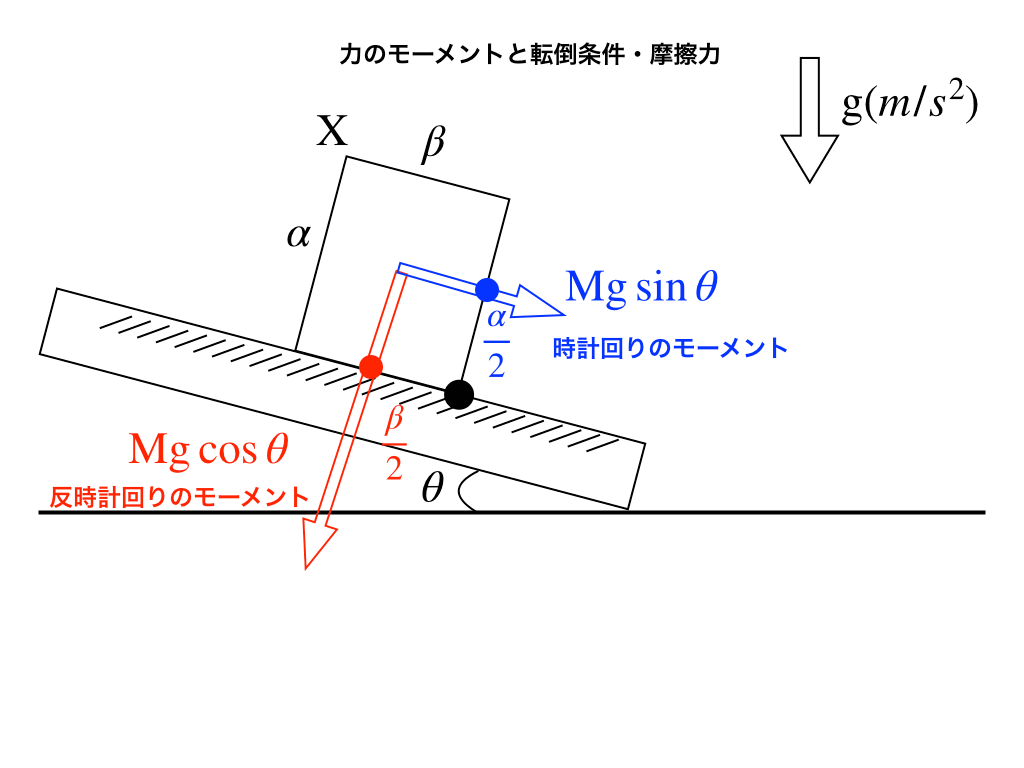
ウデの長さ(掛ける)力=モーメントより
・時計回りのモーメント:\(\frac{\alpha}{2}\cdot Mg\sin\theta\)
・反時計回りのモーメント:\(\frac{\beta}{2}\cdot Mg\cos\theta\)
ここで、すべらず(並進運動はせず)回転運動を始めるためには、
・静止摩擦力≧Mg sinθ、かつ
・時計回りのモーメントが、反時計回りのモーメントよりも大きくなくてはなりません。
∴ \(Mg\mu\cos\theta≧Mg\sin\theta\)
より、\(\mu≧\tan\theta\)
かつ
\(\mathrm{\frac{\alpha}{2}\cdot Mg\sin\theta}\)>\(\mathrm{\frac{\beta}{2}\cdot Mg\cos\theta}\)
よって、
$$\frac{\beta}{\alpha}<\tan\theta$$
これらを考えると、答えとなる条件は
$$\mu>\frac{\beta}{\alpha}$$
・・・(了)
力のモーメント・つりあいのまとめ
はじめにも書きましたが、この範囲は案外スルーされがちです。
しかし、難関大の力学分野の問題では、モーメントの考え(回転運動)が必要となる出題が少なくありません。
苦手意識のある人も、少しずつこのような問題に触れていくようにしましょう。
関連記事と続編(重心+今回の応用)へ
「(作成中です)重心の位置とさまざまな物体での演習」
最後までご覧いただき有難うございました。
弊サイト:スマホで学ぶサイト、「スマナビング!」では、読者の皆さんのご意見・ご感想の募集・記事のリクエスト(記事に付いては、対応出来ない場合もあります。)をコメント欄で行なっています。
・お役に立ちましたら、B!やシェアをしていただければ、とても励みになります。
・【お問い合わせ/ご依頼/その他のご連絡】は、ページ上部の【運営元ページ】よりお待ちしております。

