
ベクトルは理解しづらい?
このサイトのアクセスをみると、ベクトルの記事を探して来てくださる方がとても多いです。それだけ『ベクトルを苦手な人が多い』事が分かります。
そこでこのサイト内のベクトルの解説記事を集めたので、是非ご利用ください!
最終更新日:2025/04/20
ベクトルが新過程移行に伴って数学Bから数学Cに移動しました。
内容の変化は特にありませんが、今後も随時更新・新記事を作成していきます。
ベクトルとは?〜導入編〜をこのページに追加しました。
ベクトルが苦手な人は、導入編をよんでから各記事を見ていただくと理解が早く進みます。
↓クリック/タップすることができる目次↓
ベクトルとは?知識0から学ぶ記事の使い方
以下にこの記事の使い方を整理しました。
<ベクトルの特定の分野が分からない人へ>
このページに掲載されている記事の中から、分からない分野の記事を読んでみて下さい。
理解出来ればOKです。
但し、意外とその分野ではない所が分かっていない事があります。
その際は一旦ここに戻って、一から読み直してみて下さい。
<分からない所が分からない!!と言う人へ>
まず、この下の「ベクトルの知識の導入」を先に読んで、次に、このページに並べている順に、記事を上から全部読んでみて下さい。
一気に読まなくても問題ありません!少しづつでも読み進めて行くときっと役に立つはずです。
なお、ベクトルの解説記事は現在進行形で制作しているので、たまにこのページを覗いて貰えると新しい記事が増えていると思います。
又、「この分野を解説して欲しい」という記事リクエストや質問、その他お問い合わせは一番下のコメント欄にお願いします。
ベクトルの知識の導入(意味と足し算・引き算・分解)
以下にベクトルについての記事を並べていますが、その前にここで「そもそもベクトルとは何か」を簡単に紹介しておきます。
ベクトルとスカラーの違いとは
ベクトルとは、「向き」と「大きさ」という二つの「情報」を持っている矢印のことです。
それに対して、これまで我々が扱ってきた「数」という一つの情報しか持っていないものを「スカラー」と言います。
これだけでは?な人もいると思うので、筆者が良く使う例え話をします。
Aさんは友人のB君の家へ行くためにB君の家の最寄りの駅に到着しました。
ココから家へ向かう為にB君が教えてくれたのは、「駅から300m歩いたところに僕の家があるよ!」
でした。この伝え方には「300m」という一つの情報しか含まれていません=(スカラー量)。
従って駅から半径300mの円周上を歩いて探さなければいけません。
対して、「駅から真東に300mのところが僕の家だよ。」と教えてくれたとしたらどうでしょう。
「方向=真東」、「距離=300m」の二つの情報が含まれている(=ベクトル量)ので、AさんはピンポイントでB君の家へ向かう事ができます。
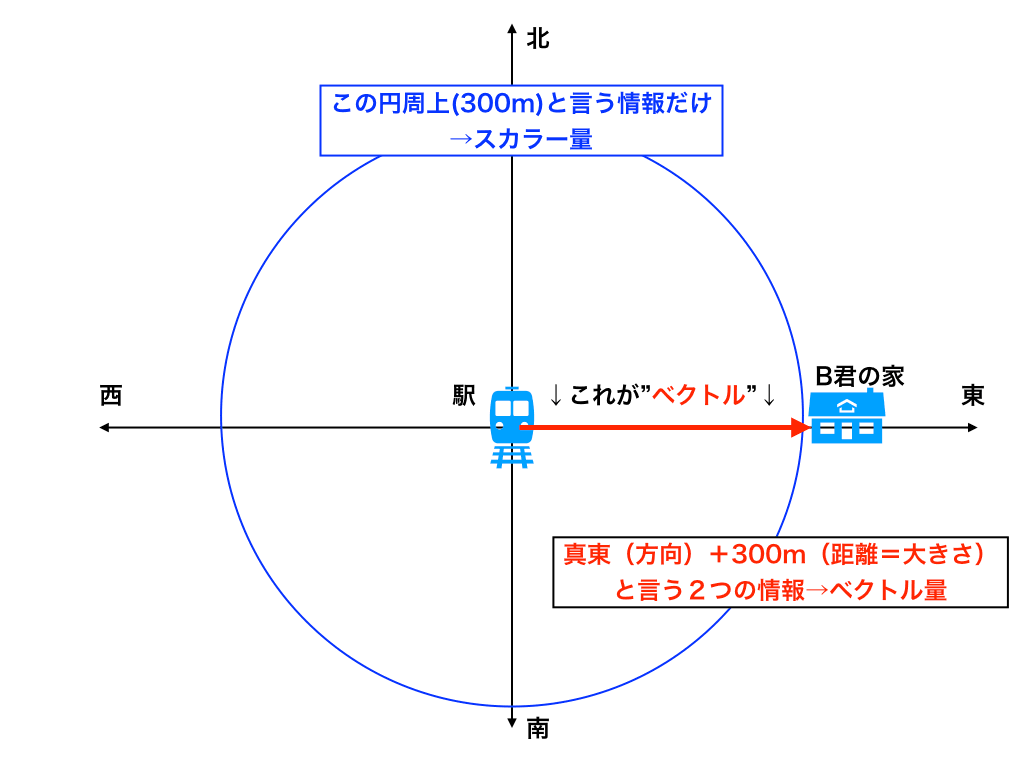
この違いがベクトルの理解への第一歩です。
(『ベクトルが違う』というフレーズが(人やチーム・会社などの”みている向きが違う”といった意味で)よく使われていますが、上で解説した通り『ベクトル』は大きさもあわせ持つので、数学的には誤った使い方であることがわかります。)
「線分/直線/半直線」と「有向線分(=ベクトル)」の分類
次にこれまで「線」と言われていたものが四種類に分けることができて、そのうちの一つがベクトルであることを図解します。<下図>
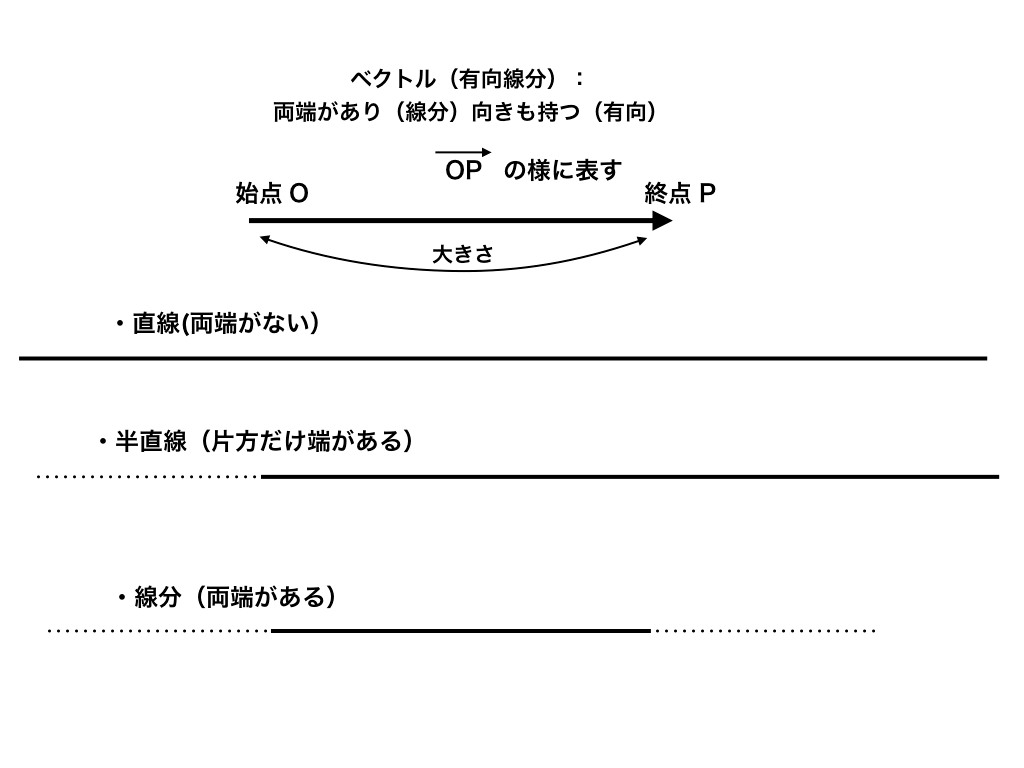
<直線・半直線・線分・有向線分>
要するに、ベクトル=有向線分(向きがある+線分(両端があり、大きさが無限では無い)ということです。
ベクトルの相等、逆ベクトルについて
これも以下の図中で解説しています。
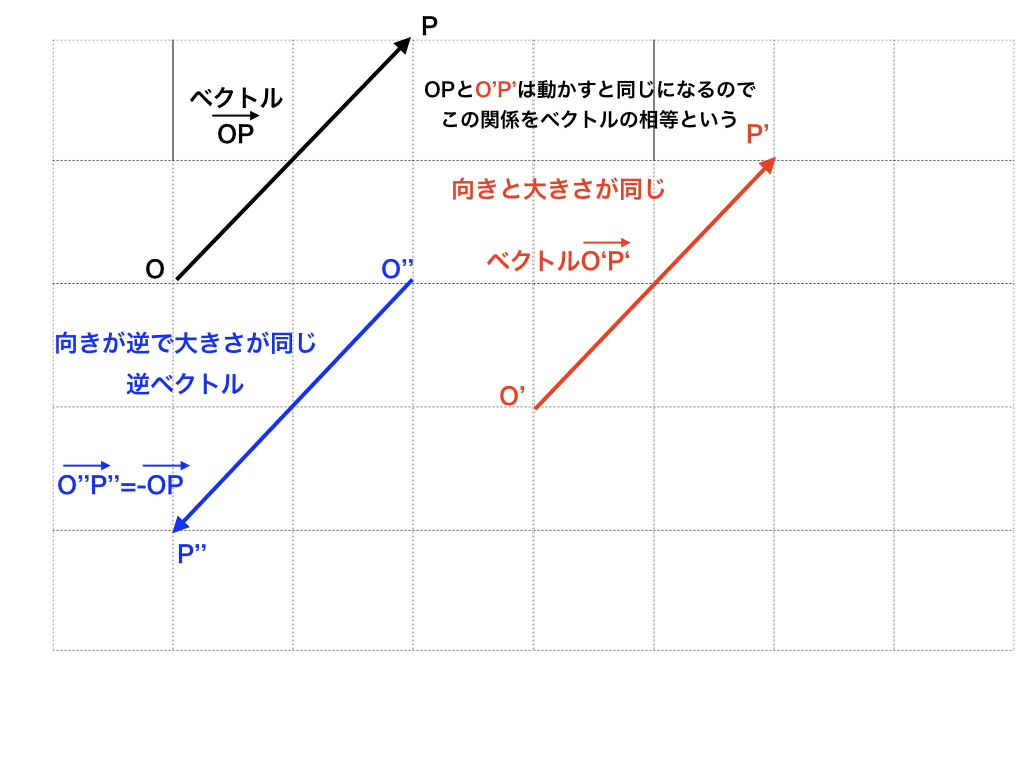
<ベクトルの相等・逆ベクトル>
赤のベクトルは動かすと黒のベクトルと重なります。ベクトルは、自由に動かして同一となるものは同じとみなします。
これを「ベクトルの相等」と言います。
また、青のベクトルの様に、向きが180度違うが、大きさは黒のベクトルと同じものを「逆ベクトル」と言います。
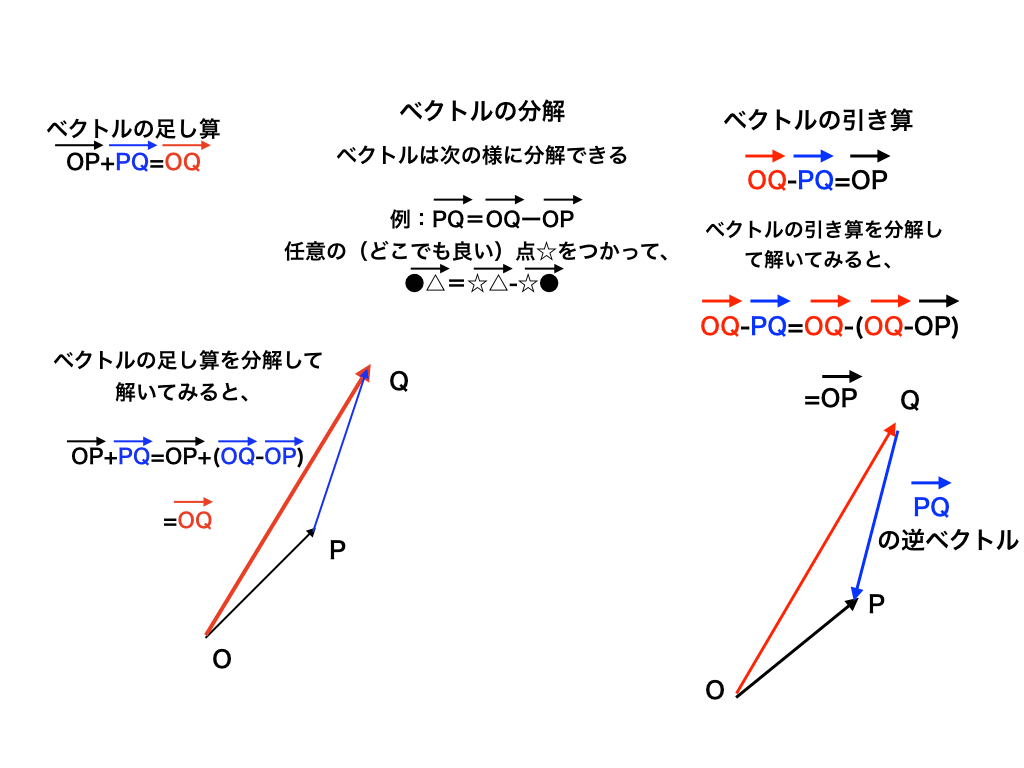
ベクトルの足し算と引き算
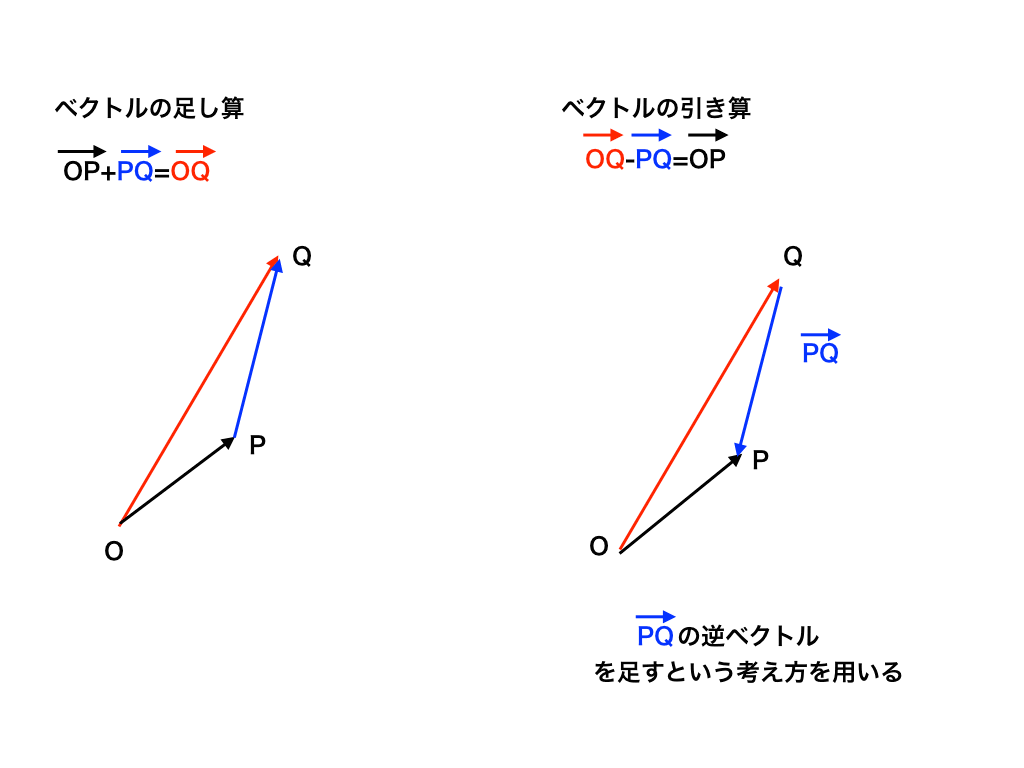
ベクトルの足し算/引き算は上の図のように行います。(一部修正しました。2020/03/01)
ベクトルの分解とは(図解)
「ベクトルの分解」は別に記事を作っています(下のリンクにあります)が、キソのキソはここで図解します。
ベクトルは導入部分がこれまでの数学と少し異なっていて大変ですが、
一度理解すると中学での幾何や数学Aの平面/空間図形のような範囲を単純計算で解いて行く事ができるようになります!
では、ベクトルの導入編を頭に入れたら、以下の記事を一つ一つ読んでいってください。↓
ベクトルの解法解説記事13選!+α
ここからは、ベクトルの問題を実際に解いて行く際に必須の解法やテクニック・コツを解説した記事13選をまとめました。
ベクトルって何?ーベクトル基礎の基礎ー
この記事では、ベクトルの知識が全くない人でもキソを理解して、次のステップへ進めるよう
になるべく丁寧に「ベクトルとは?」を解説しています。
位置ベクトルとベクトルの分解
位置ベクトルとは一体なんなのでしょうか?
簡単にいうならば、座標上のある点をベクトルの矢印の先の点と対応させるのですが、詳しくは以下の記事にて・・・
ベクトルPA+PB+PC=0型の点Pと面積比
頻出の重要問題である、『三角形の辺や内部に存在する点P』や『面積比』を求める方法を「ベクトルの和・差で表される条件式から点Pを求める解法」で詳しく解説しました。
イラストと複数の練習問題付き。
「係数の和が1」になる条件と理由
いわゆる「係数の和が1」(OP=sOA+tOB のsとtが係数で、s+t=1になること)を利用することで、ベクトルの問題が簡単に解けることが非常に多いです。
この記事では、その条件と理由・使い方を解説しています。
一次独立の意味がわからない人へ
『一次独立』と『ベクトル方程式』はイマイチよく分からない人が大変多いです。
しかし、名前ほど複雑ではないのでぜひ以下の記事で理解しましょう!
(一次独立は、共面条件をはじめ様々なベクトルの問題を解く際にかならず必要になります)
ベクトルの終点の存在範囲の問題解説
ベクトルの先(矢印)の点(終点)が動くことによって、その点の軌跡は線や面になり(存在範囲)、さらにその面積などを求めさせる問題はよく出題されます。
「ベクトルの終点の存在範囲の問題を得意にする為の2step」の記事では、そんな問題への対処法を解説しています。
終点の存在範囲(2)
続編となる第二回では、与えられる条件式が不等式の場合に、
その領域を図示する方法と領域の面積を求める問題を紹介しました。
「存在範囲の応用編:ベクトルの終点が領域を描く条件式の問題の解き方」
共面条件と共線条件の意味とは?
点が同一線/面にあるための条件について:「共面条件と共線条件の解説と演習問題」:で詳しく解説しました。
ベクトルの内積について
ベクトル同士の掛け算は「内積(・)で表します」と「外積(×)で表します」の2つがあります。
特に内積は、ベクトルに関係する問題のほとんどで必要になる演算なので、以下の記事でしっかりと理解しておきましょう!
(なお、外積については5つ下の項で解説しています)
正射影ベクトルの意味と応用
正射影ベクトルについて詳しく解説:「正射影ベクトルの公式とその応用問題の解法」しています。
利用法を学んで差をつけましょう。
ベクトル方程式とは何か?よく分からない人へ
位置ベクトルとともに、初めてベクトルを学ぶ人が困惑する『ベクトル方程式を1から解説』しました。
記事を読み進めると、何も特別なことは言っていないことが理解できるはずです。
平面に垂直なベクトルの条件
垂直条件だけでなく、過去問を使ってこれまでのベクトルの総復習ができる問題と解答解説を掲載しています。
【ベクトルの総復習】平面に垂直なベクトルの条件と空間ベクトルの良問
【空間】平面の方程式の求め方(ベクトル方程式の応用)
空間ベクトルのさらなる応用分野である、「平面・球面の方程式etc,,,」の第一回目として、
・平面の方程式の求め方をベクトル方程式&一次独立の応用型と、
・外積・法線ベクトルを用いた発展型の2タイプに分けて詳しく解説しています。
【応用】ベクトルの外積
ここでは、高校範囲外ですが、知っておくと大変役に立つ、
ベクトル同士のもう一つの掛け算「外積」についてイラスト付きで詳しく解説しました。
「ベクトルの外積とは?内積以外のベクトル同士の掛け算の正体」
【空間】球面の方程式の求め方
上の、平面の方程式に続いて球面について方程式・球面のベクトル方程式の求め方を解説しています。
確認問題つき。「【空間ベクトル】球面の方程式の求め方と応用問題【数B】」
接平面や2つの球が作る円の方程式
球面の方程式の発展編です。2つの球体が重なった時にできる「円」の方程式や、球体が空間中で平面と接する時、その「接平面」の方程式の作り方を3Dのイラストを使って詳しく説明しました。
法線ベクトルと空間図形への応用
「法線ベクトル」を使って、2直線や2平面のなす角を求めたり、ある平面に関して対称な点の座標を求めるような応用問題の解き方を解説しました。
物理/物理基礎でのベクトルの利用
各学校のカリキュラムの関係で、ベクトルや三角比を習う前に、物理基礎(特に力学)でその知識が必要となることがあります。
そんな人のために、物理基礎を学ぶのに必要十分な『ベクトル』について解説しました。
線形代数など関連/重要範囲総まとめページ
ベクトル範囲以外で、悩んでいる人が多い分野を解説した記事のまとめページを作りました。それぞれのページへ行ってニガテな単元の記事をご覧下さい!
ベクトルから線形代数学の基礎へ
(高校数学B→現行課程では数学Cへ移動しました)でのベクトルを学んで面白いと思った方は、その応用分野(旧々課程では数学Cで行列が教えられていました)である“線形代数”を学んでみましょう。
「線形代数を高校レベルで学ぶ記事まとめ」:上級者向きですが、なんとなく解いていた(使っていた)ベクトルの成り立ちから意味、さらに”コーシー・シュワルツの不等式”などが本質的に理解できる記事を揃えました。
三角関数の公式の証明/導出法一覧
三角関数の公式を丸覚えしていませんか?三角関数の公式は最重要&量が多い&ヤヤコシイので、丸暗記は得策ではありません!
導き方を理解してその場その場で創り出す事(公式を覚えるのではなく、導き方を覚えて習得すること)が大切です。
以下のまとめ記事では、高校数学で必要な三角関数の公式をすべて網羅しています。
場合の数と確率の解説記事
一つ下のまとめと共にある意味「特殊」な分野である「場合の数と確率」は、正しい考え方が出来るか否かで、0か100かになるほど、差がつきやすい分野です。
逆に場合の数と確率を得意に出来れば、理系/文系を問わずかなりのアドバンテージを得られます。
数列の漸化式の解き方シリーズ
漸化式の解法を網羅しています。確率、極限にも使われる重要分野なので、ぜひうまく利用してどの様な漸化式でも解ける様になりましょう!
整数問題の攻略法まとめ
「整数」も場合の数と確率同様に難しい分野ですが、以下のまとめでは閃きやセンスが無くとも点を取っていく方法を載せています。
極限分野の記事6選!
現在数列の漸化式の解き方シリーズを作成中です。<作成しました>
ベクトルについても引き続き随時更新していきます。

