ベクトルの"和や差"の条件式から点Pの位置や面積比を求めるコツ
\(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\vec{0}\)
<この記事の内容>:タイトルにもあるように、\(\vec{●A}+\vec{●B}=\vec{●C}\)と言うようなベクトルの和・差の式から、点●(●=Pの場合がほとんどです)がどのような位置にいるのか問われる問題について解説しました。(+αとして『面積比』の問題も追加しました)
<この記事の対象>:『解答』には「三角形の中や、線分上の△:◯に内分したところに点がある」、と言う風に書かれているが、イマイチ理解できなかったり、自力で答えを導けない人。
<ベクトルの関連記事まとめ>:予習・復習に「ベクトルとは?0から応用まで厳選記事総まとめ!」をご利用ください。
目次(タップした所へ飛びます)
PA+PB+PC=0タイプの問題の解法
このタイプは頻出な上、少し解答の流れのコツを知っておかないと思いつかない問題もあるので、具体例をもとに解説します。
始点を揃える(ベクトルの分解)
この手の問題は、まず初めに始点を揃えると言う操作を行うことがほとんど必須なので、それを行います(詳しくは「位置ベクトルと"ベクトルの分解"をわかりやすく!」)。
中点を表す:もっとも基本的な例題
例題1:三角形ABCにおいて、\(\overrightarrow{PB}+\overrightarrow{PC}=\vec{0}\)の時、点Pの位置を示せ。
解説1:始点を”A”に揃える
すると、\(\vec{AB}-\vec{AP}+\vec{AC}-\vec{AP}=\vec{0}\)となって、(右辺)に\(\vec{AP}\)を集めると
\(\vec{AB}+\vec{AC}=2\overrightarrow{AP} \)ここで、APの矢印の先である点Pを知りたいので、APの係数を”1”とするように、両辺を2で割ります。
すると、$$\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}=\frac{1\cdot \overrightarrow{AB}+1\cdot \overrightarrow{AC}}{1+1}$$
のように式変形ができるので、これはBCを1:1に内分、つまりBCの中点が点Pである事がわかります。
したがって、『点Pは線分BCの中点である・・・(答)』
内部点/外分点の公式の利用
次の2例題も、基本的な流れは例題1と同様です。
例題2:\(\overrightarrow{PB}+4\overrightarrow{PC}=\vec{0}\)の時の点Pの位置を答えよ。
例題3:\(2\overrightarrow{PC}-\overrightarrow{PB}=\vec{0}\)である場合の点Pの位置を答えよ。
解説と公式の再確認
解答解説2:『まず始点をAに揃え、APを(右辺)へ、それ以外のベクトルを(左辺)に集めたうえで係数を整理する。』この指針(*)は常に変わりません。
\(\overrightarrow{AB}+4\overrightarrow{AC}=5\overrightarrow{AP}\)
【ここから最重要ポイント(1)】両辺を5で割りますが、ABとACの係数(1と4)に注目します。
すると5で割ると言う事は、次のように表すことができます。
\(\frac{1\cdot \overrightarrow{AB}+4\overrightarrow{AC}}{4+1}=\overrightarrow{AP}\)
この左辺は、BCを4:1に内分した時の式と同じです。
すなわち、点Pは線分BCを4:1に内分した点である。・・・(答)
『5で割る→(4+1)で割る→内分の公式が使える!』
と言う流れ(**)が重要なので、しっかりと頭に入れておいて下さい。
解答解説3:上でも紹介した指針(*)に沿ってここでも式変形していきます。
\(2\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{AP}\)
これはAPの係数が1ですが、(**)の流れと同じ様に出来ないか考えてみます。
ABとACの係数がそれぞれ「-1」と「2」であることに注目すると、【両辺を1で割る(=2-1)で割る】ことに書き換えることができます。
したがって、$$\frac{(-1)\cdot \overrightarrow{AB}+2\overrightarrow{AC}}{2-1}=\overrightarrow{AP}$$
これは外分点の公式です!
よって、点Pは線分BCを2:1に外分した点である。・・・(答)
内分・外分の式が使えない(分母/分子の数が合わない)場合
ここまでは、うまく中点や内分点・外分点の公式が使える比較的簡単な問題でした。
次に、頻出問題である公式がうまく使えない、(=分母と分子のベクトルの係数が揃わない場合)の点Pの探し方を紹介していきます。
応用問題1:\(3\overrightarrow{PA}+\overrightarrow{PB}+2\overrightarrow{PC}=\vec{0}\)の時、点Pの位置を答えよ。
応用解説1:上手く分母を合わせるコツ
とりあえず指針(*)に従って式を整理してみます。
\(\overrightarrow{AB}+2\overrightarrow{AC}=6\overrightarrow{AP}\)
ここで問題が発生します。APの係数が「6」なのに対して、左辺の係数は「1と2」であり、どう頑張っても内分・外分のカタチに持っていくことが出来ません。
帳尻を合わせる→(三角形の内部の点である!)
そこで、【最重要ポイント(2)】:AB/AC の係数はそのままにして、式の一番前に『分母が6』となるように調節する分数を掛け合わせる。
言葉だけでは???となってしまう人も多いと思うので、以下で実際に式変形していきます。
$$\frac{3}{6}\cdot \frac{\overrightarrow{AB}+2\overrightarrow{AC}}{2+1}=\overrightarrow{AP}$$
さて、(左辺)に6分の3を持ってきて、ベクトルの部分はこれまでの流れ(**)通り2:1に内分する式を作り出します。
すると、丁度APの係数が1となって、例題1、2とほぼ同じ形にする事ができました。
また、この式を6倍して左辺を整理すると、元々の式\(\overrightarrow{AB}+2\overrightarrow{AC}=6\overrightarrow{AP}\)に戻る(=つまり同じ式である)ことも理解出来るのではないでしょうか。
では、新たに作り出した式を日本語に直してみると、『線分BC』を2:1に内分した点をP’とするとAとP'を1/2倍したところ(=線分『AP'を1:1に内分したところ』)が点Pである、と言う風に理解する事ができます。
ゆえに、線分BCを2:1に内分した点と点Aの中点が点Pである・・・(答)
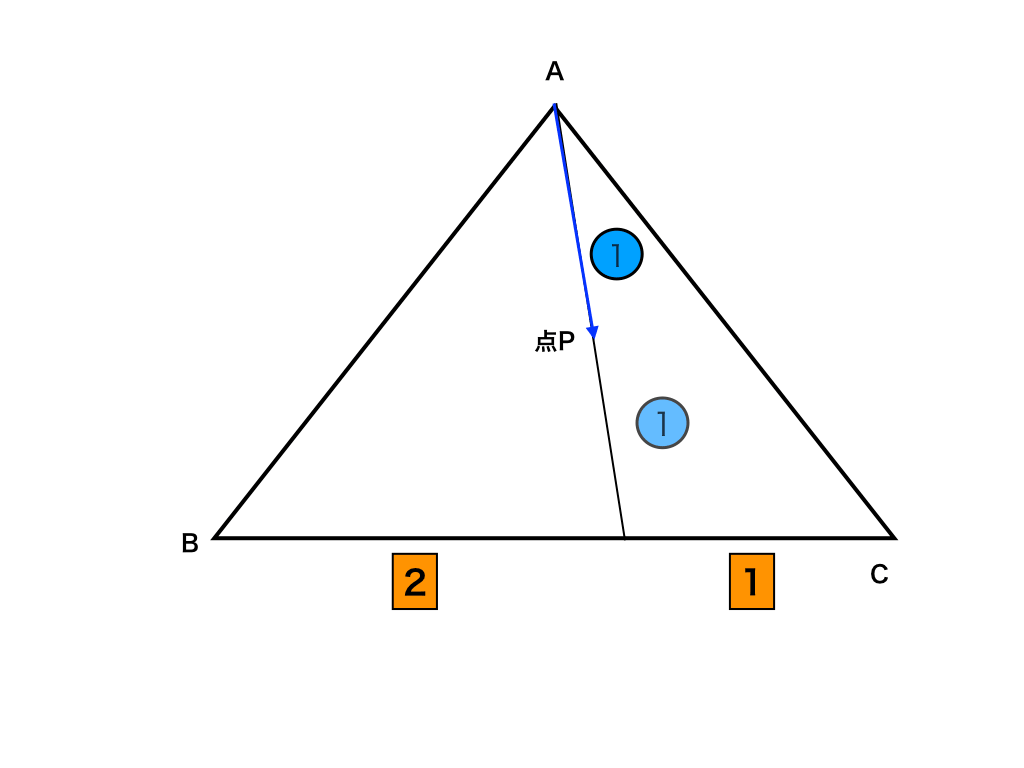
<参考:点Pの位置のイラスト>
応用確認問題2(+面積の比)
応用問題2:\(18\overrightarrow{QA}+35\overrightarrow{QB}+7\overrightarrow{QC}=\vec{0}\)の時、点Qの位置と、△ABQ:△AQC:△BQC:△ABCの面積比を求めよ。
解答・解説2
面積比の問題が追加されていますが、それは次の項で解説するとして、まず点Qの位置を求めてみましょう。
本問は『係数が若干複雑+求める点がQ』ですが、実際にやることは応用例題1と同じです。
まず、いつも通りAに揃えて整理すると\(35\overrightarrow{AB}+7\overrightarrow{AC}=60\vec{AQ}\)
係数があっていないので、両辺を60で割ったのちに(ベクトルの式)の係数部分を調整します。
$$\frac{42}{60}\cdot \frac{35\overrightarrow{AB}+7\overrightarrow{AC}}{7+35}=\vec{AQ}$$
もう少し式を簡単にして、$$\frac{7}{10}\cdot \frac{5\cdot \overrightarrow{AB}+1\cdot \overrightarrow{AC}}{1+5}=\vec{AQ}$$
ゆえに、点Qは、点Aと線分BCを1:5に内分した点とを7:3に内分した点である。・・・(答)
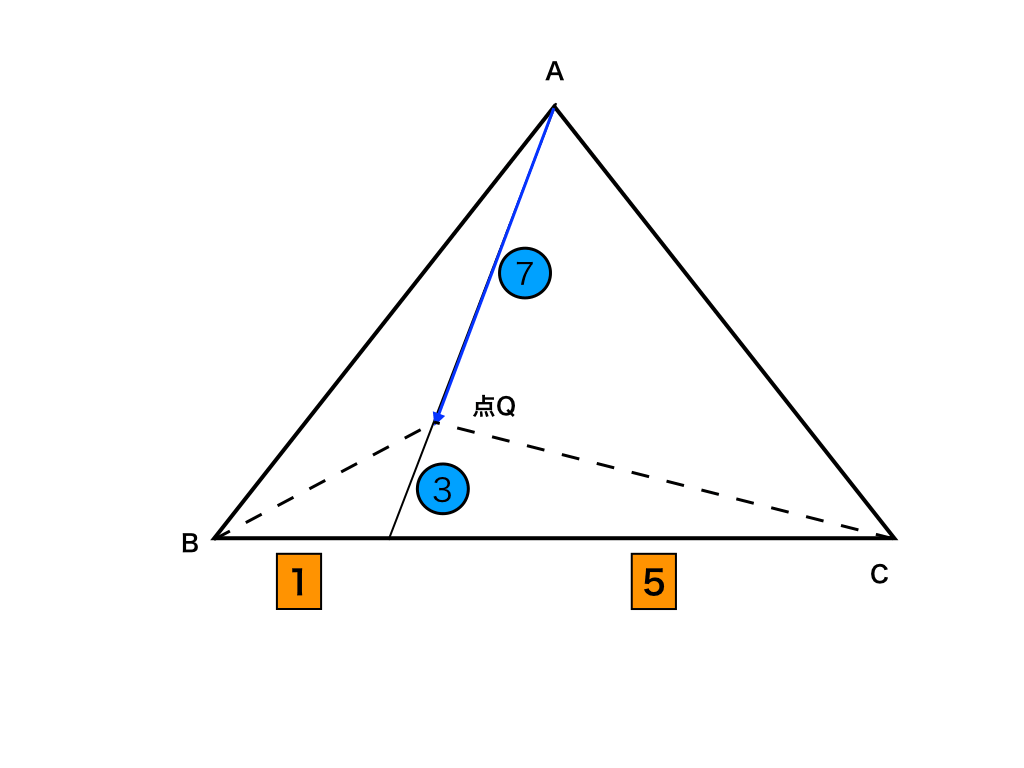
<参考イラスト2:点Qの位置>
面積比の求め方
さてここからは、△ABQ:△AQC:△BQC:△ABCの『面積比』を計算していきます。
上の項で掲載した<参考イラスト>を見ながら面積の比を計算します。(以下BCを1:5に内分した点をRとします。)
まず、△ABRはBR:RCが1:5なので、△ABCの面積の1/6。
△ABQはAQ:QR=7:3より$$△ABCの\frac{1}{6}\times \frac{7}{10}=\frac{7}{60}\times △ABC$$
△AQCも同様に計算すると$$△ABCの\frac{5}{6}\times \frac{7}{10}=\frac{35}{60}\times△ABC$$
△BQCはAQ:QR=7:3より、△ABCの7/10
以上3つの面積が計算できたので、△ABQ:△AQC:△BQC:△ABC=7:35:18:60・・・(答)
今回のまとめと関係のある記事
今回のメインは、うまく『分母・分子の数が合うように、先頭に”帳尻合わせのための分数”を持ってくる』と言う点です。
他の問題でもこのような柔軟な考え方は必要になってくるので、ぜひ復習して身につけておきましょう。
また、【中点・内分・外分の公式】や、それらの位置の図示がしっかり出来ているか、そのあたりもよく確認しておきましょう。
ベクトルのまとめ記事一覧
総まとめ:「〜ベクトルとは?ゼロから発展レベルの解法まで〜」←ベクトルで分からない事があれば、この記事の中に該当するものがないか探してみて下さい。
外分点の図示が苦手な方は、、「外分点を図示できますか?イラスト付きで確実にマスター」をぜひ確認しておきましょう。
今回も最後までご覧いただき、ありがとうございました。
弊サイト:「スマホで学ぶサイト、スマナビング!」では、読者の皆さんのご意見・ご感想の募集をコメント欄にて行なっています。
お役に立ちましたら、B!やシェアなどをしていただけると、大変励みになります!
・その他のお問い合わせ/ご依頼等は【運営元ページ】よりお願い致します。

