
球面の方程式と球面のベクトル方程式の求め方
・この記事では、空間ベクトル最後の壁「球面の方程式」とその応用問題を解説しています。
目次(タップした所へ飛びます)
球面の方程式を求めよう
※「平面の方程式の求め方」の続編なので、未読の方は先にご覧下さい。
さて球面の方程式の求め方には、空間ベクトルを利用する方法が2通りあり、どちらも非常に大切なのでその仕組みを理解しておきましょう。
中心からの距離が一定を使う
球の中心から球面(球の表面)上のどの点まででも、その距離は一定=半径rとなります。(これは、円のベクトル方程式の場合と同様です。)
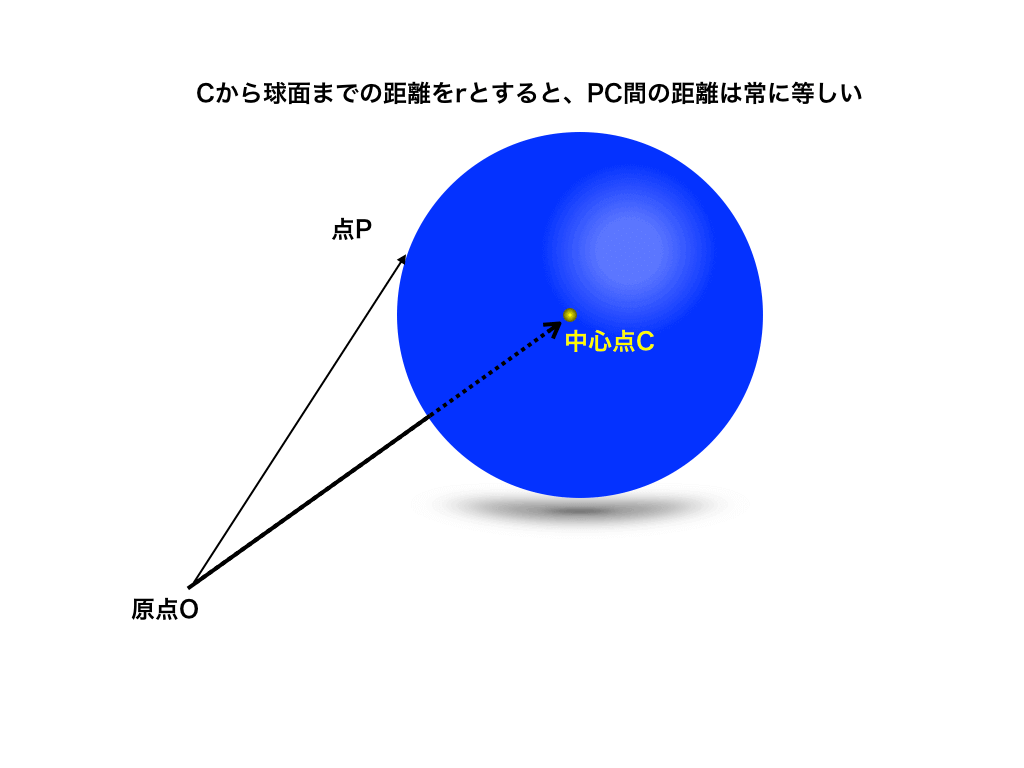
<球面とその中心>
そこで、球面上の点Pと中心点Cの位置ベクトルを使って、球面のベクトル方程式を以下のようにあらわすことができます。
$$|\vec {p}-\vec {c}|=r$$
さらに、点Pの座標を(x,y,z)、点Cの座標を$$C:(c_{x},c_{y},c_{z})とすると、|x-c_{x},y-c_{y},z-c_{z}|=r$$
両辺二乗すると、絶対値が外れて
$$(x-c_{x})^2+(y-c_{y})^2+(z-c_{z})^2=r ^2・・・(*1)$$
これで球面の方程式を導くことができました。
また、(*1)の式を展開して、x、y、xの係数と定数項に適当な文字a,b,c,dをおいた
$$x^{2}+y^{2}+z^{2}+ax+by+cz+d=0$$も球面の方程式になります。
(*1)の式は、同様の方法で求めることができる、円の方程式とそっくりです
$$【円の方程式:(x-c_{x}) ^2+(y-c_{y}) ^2=r ^2】$$
球の直径の両端とする2点とタレスの定理から導く
次は、球面上の2点が与えられ、かつその2点が球の直径の端である場合です。
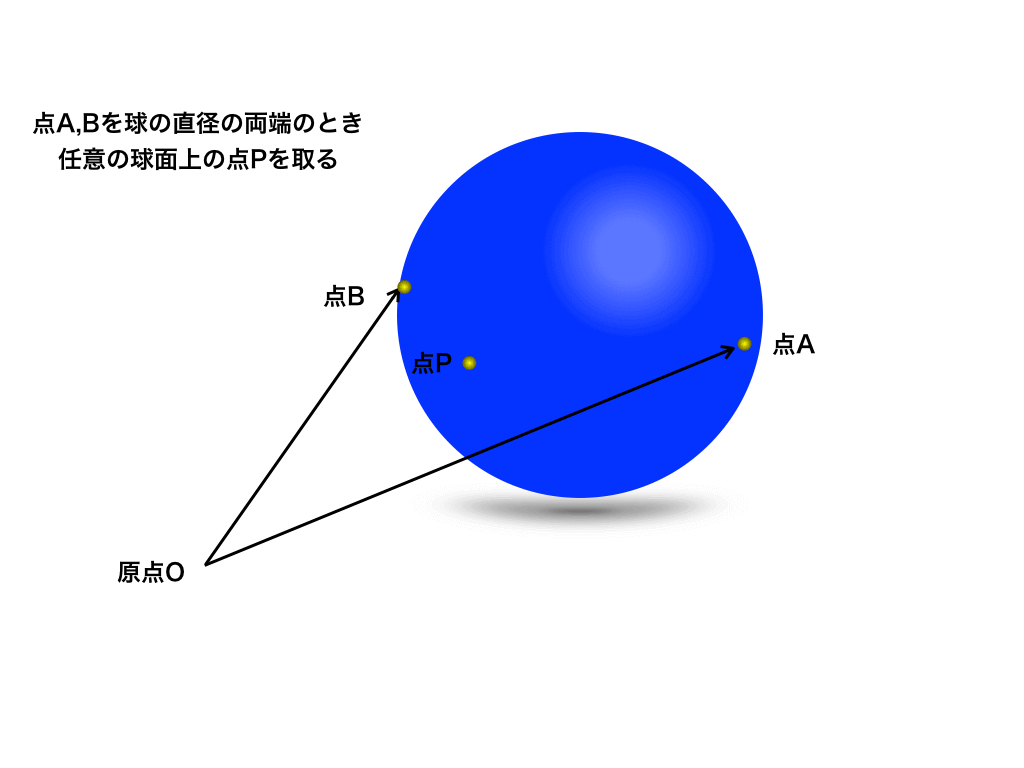
<球面上の2点>
このとき、ABが直径の両端であることから、タレスの定理(=円周角の定理)を使い、
点Pをベクトル方程式であらわすことを考えます。
タレスの定理とその利用
「タレスの定理」と聞くと難しそうですが、簡単に説明すると「円周角の定理」の中心角が180°の時のことを言います。
この定理を利用して、球面の方程式をベクトルを使って表していきます。
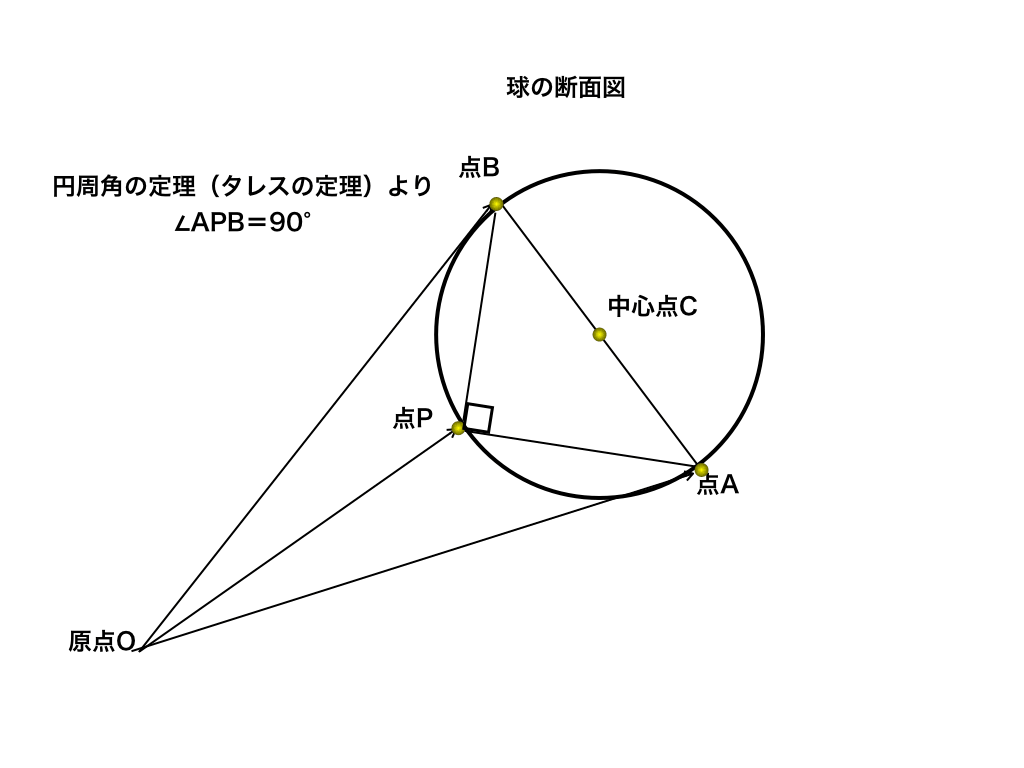
<タレス(円周角の定理)と球面の方程式>
まず、点Pへの点Aからのベクトル$$\vec{AP}$$と点Pへの点Bからのベクトル$$\vec{BP}$$がタレスの定理より
$$90°= \vec{AP} ⊥\vec{BP}$$であることを利用して、垂直である⇔内積は0!を思い出して
<参考:「ベクトルの内積が分かる!ベクトル同士の掛け算の正体」>
$$\vec{AP} \cdot \vec{BP}=0$$
変形すると、$$(\vec{p}-\vec{a}) \cdot (\vec{p}-\vec{b})=0 $$
球面のベクトル方程式はこの形でもあらわす事ができます。
球面の方程式の問題
球面の方程式と、ベクトルの関係がわかったところで関連問題を解いていきます。
方程式を求める練習問題
以下の(1)〜(3)の条件の時、それぞれの球面の方程式を求めよ。
(1):4点P(1,1,1)、Q(2,0,1)、R(0,0,3)、S(1,2,2)が同一球面上にある時
これは、球面の方程式の一般形(x2+y2+z2+ax+by+cz+d=0)に4点の座標を代入して、未知数を消していく事で解く事ができます。
未知数がa.b.c.dの4つに対して、4つの座標が与えられているので必ず解けます。(一度やってみて下さい)
A.$$ x^{2}+y^{2}+z^{2}-3x-y-5z+6=0$$
(2)点S(3,4,3)、点T(5,6,5)が球の直径の両端である時
まず、球の中心点の座標を求めるために、点S・Tの中央に位置する点の座標を求めます。
(2点は直径の両端なので、その2点の真ん中の座標は球の中心となります)
ST間の中心を点Cとおくと、$$C=\begin{pmatrix}
\frac {3+5}{2} \\
\frac {4+6}{2} \\
\frac {3+5}{2}
\end{pmatrix}=\begin{pmatrix}
4 \\
5 \\
4
\end{pmatrix}$$
この作業で(x-4 )2+(y-5 )2+(z-4 )2=r2
の式のうち、r2以外が埋まり、残りの半径rは、空間座標での2点間の距離の公式によって、|ST|を求め、
その半分を計算することで求まります。
$$|ST|=\sqrt {(5-3)^{2}+(6-4)^{2}+(5-3)^{2}}=2\sqrt {3},r=\sqrt {3}なので、$$
(x-4)2+(y-5)2+(z-4)2=3・・・(答)
(3)中心点Cの座標が(3,2,2)で、球面の方程式で「(x-5)2+(y-4)2+(z-3)2=16」と表される球に内接する時
「図形と方程式」の分野で、円と円の距離や内接・外接を学んだかと思います。この問題は、その3球体versionです。
手順は、
1;2つの球体の中心点間の距離を調べる。
2;求める球の方程式を()2+()2+()2=r2の形に変形する
3;大きい方の球の半径の二乗=16より、半径は4=中心間の距離+求める球の半径になる。
(解答)2球体の中心間距離は、$$\sqrt {(5-3)^{2}+(4-2)^{2}+(3-2)^{2}}=3$$
$$(x-3)^{2}+(y-2)^{2}+(z-2)^{2}=r^{2}と、4=3+r より、$$
$$(x-3)^{2}+(y-2)^{2}+(z-2)^{2}=1・・・(答)$$
球面の方程式の条件問題
球面の方程式を満たすためには、当然r=半径が0より大きい必要があります。
r=0の時は、球の大きさが0となり「点」に、r<0の時は条件を満たしません。
(問題文を訂正しました)
以下の方程式のうち、球である条件を満たすものを選べ。
(1):\(x^{2}-4x+y^{2}-6y+z^{2}-2z-1=0\)
(2):\(x^{2}-6x+y^{2}-10y+z^{2}+2z+37=0\)
<解答解説>
rの値が0未満でないかチェックしていきます。
(1)を平方完成させると
(x-2)2+(y-3)2+(z-1)2=15
となって、右辺>0より球となります。
(2)同様に、平方完成すると
(x-3)2+(y-5)2+(z+1)2=-2
したがって、(右辺)=-2<0
となって、球になる条件を満たしません。
よって(1)・・・(答)
まとめと次回(球面と接平面の方程式へ)
・球面の方程式は「x2+y2+z2 +ax+by+cz+d=r2」か、「(x-a)2+(y-b)2+(z-c)2=r2 ;中心点の座標が(a,b,c)の時」で表せる。
・導出法は、球面と中心の長さが一定or球の直径の端となる2点とタレスの定理を用いる
・球面の方程式のr2がそれぞれ、r=0の時「点」/r>0の時「球」/r<0の時「無し」
平面・球面の方程式と法線ベクトルシリーズ
次回は、球と球の接平面(接線の平面バージョン)など、球面の方程式と法線ベクトルの応用問題を解説していきます。
・<第一回:「平面の方程式の求め方と法線ベクトル」>
・<第二回:「今ここです」>
・<第三回:「球面どうしが交わってできる円や接平面の方程式の求め方」>
・<第四回:「法線ベクトルの使い方と空間図形の問題への応用」>
↓↓ベクトル分野の記事の総まとめは以下よりご覧ください!↓↓
<<「ベクトルを得点源に!解法総まとめ記事」>>
お役に立ちましたら、いいね!やB!、シェアをお願いします!
記事リクエスト・誤植等はコメント欄までお寄せください

