ベクトルの終点の存在範囲2:(不等式・求積問題編)
この記事は、前回の記事→<『条件式が等式の「ベクトルの終点の存在範囲』>の続編です。
前回との違いは、条件式に不等号が入っている点と、
その存在範囲の面積を求める少し発展した問題を扱っている点です。
目次(タップした所へ飛びます)
ベクトルの存在範囲と不等式
前回の記事では、条件が全て等号(=)で結ばれている場合について解説してきました。
ではもしも条件に不等式が入った場合、どの様な事が起きるのでしょうか?
実際に例題を通して見ていきます。
問題
同一平面上に点O、A、B、Xがあり、
$$点xは\overrightarrow {OX}=s\overrightarrow {OA}+t\overrightarrow {OB}$$
を満たすものとする。
実数s、tが以下の条件のとき、点Xの動く範囲を図示せよ。
(例題1ー1) s+t=1、ただしs ,tは実数(前回のようにs≧0,t≧0の条件がありません!)
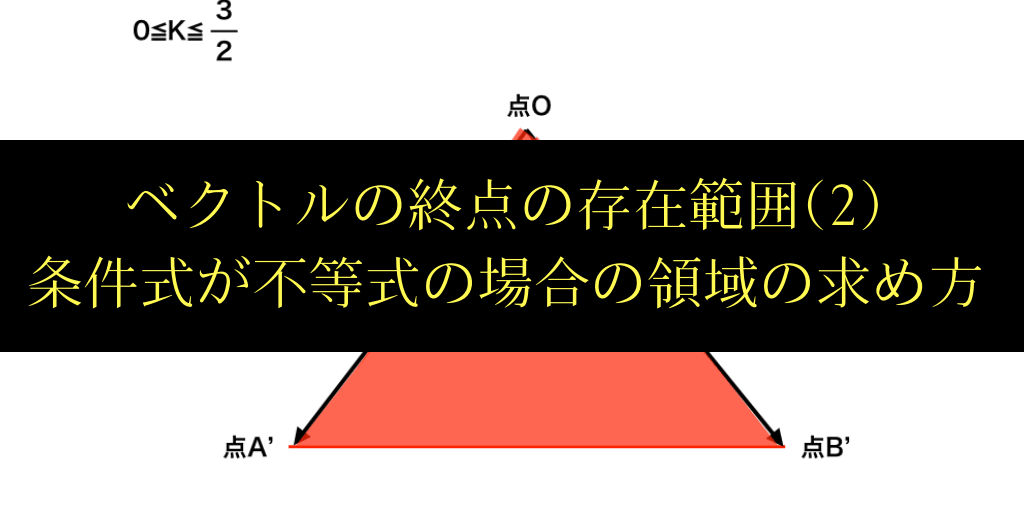
(例題2ー1) 0≦s+t≦3/2、ただしs≧0かつt≧0。
(例題2ー2)三角形OABの面積を1とする時、例題2-1で図示した範囲の面積を求めよ。
(等式で表されたベクトルの終点の復習)
この例題1については、ほぼ前回の【ベクトルの終点の存在範囲の記事(条件式が等式の場合)】と同じです。
基本的には全て”係数の和”を1に持って行くことを目的にして、変形していきます。
<参考:「ベクトルの『係数の和が1』の法則と和が1になる理由」>
(解答解説1−1)
s+t=KとおくとK=1より、$$\vec {OX}=s\vec {OA}+t\vec {OB}$$ の終点は、”直線AB”を表す。
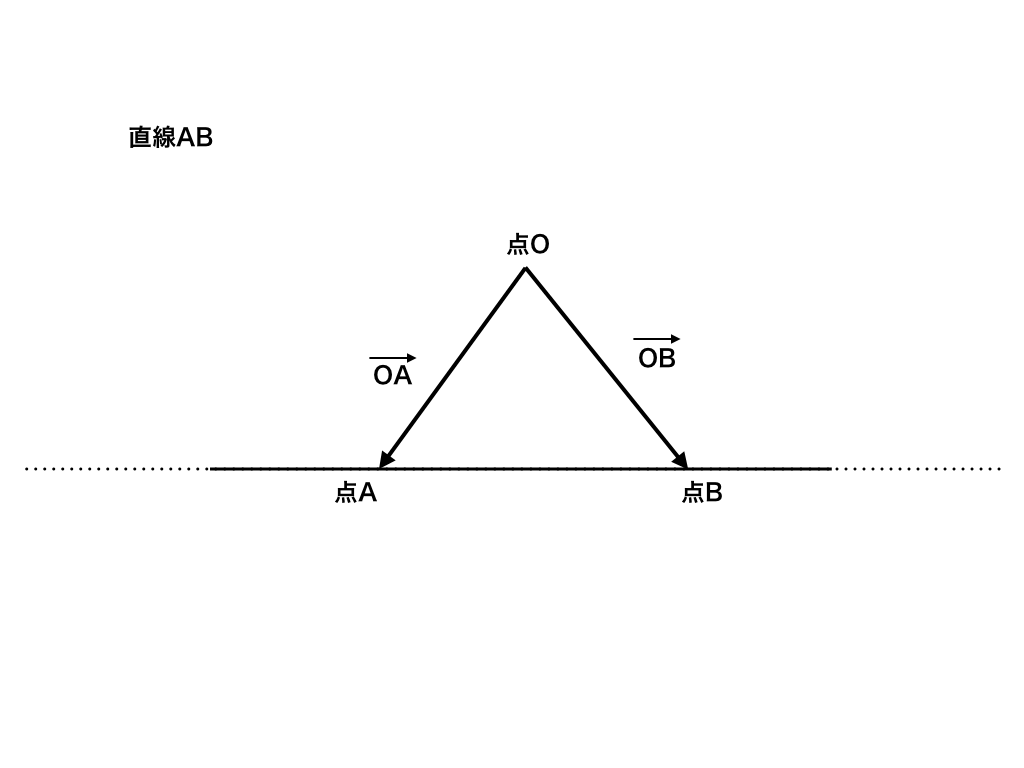 <問題1-1解答(直線AB)>
<問題1-1解答(直線AB)>
係数の条件で変わる”線分”と”直線”に注意!
注意点としては、係数の和をKとするとき
・K=1かつ、s,tがともに0以上ならば線分ABが存在範囲になるのに対して、
・K=1のみで、s、tに条件が付いていないときは”直線”AB(つまり、点A・点Bの両端から左右にずっと続いていく)ことに気をつけましょう。
(係数の範囲によって、線分が直線に変わる理由)
これは「外分」のことを考えるとわかりやすいです。
『s,tがともに≧0』の条件があれば、s=-2,t=3のように外分した点が存在範囲になることはありません。
しかし、s・tともに0以上という条件がなければ、係数の和K=1でありさえすれば良いので、
全ての外分点を含むことになります。
結果として<図1−1>のようにABの外側も含む、”直線AB”が終点の存在範囲となるのです。
さて、ここからが本題です。
係数の和の条件が不等式の場合の存在範囲
<問題2−1の解き方・考え方>
答えは、以下の図2−1の赤く塗った領域で、周囲の線上も含みます。
<図:2−1の(答)領域>
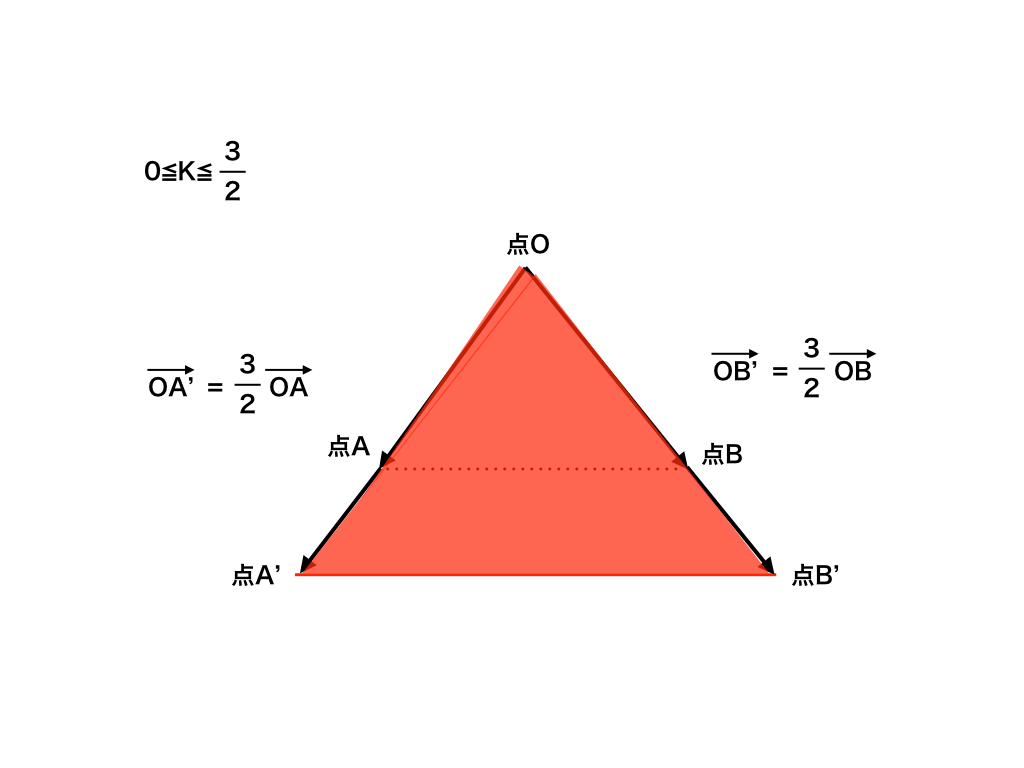
s+t=Kとおくと,条件式は右の様に表せます。0≦K≦3/2
$$ここでK≠0のもとで、s+t=KをKで割ると、\frac {s}{K}+\frac {t}{K}=1$$
$$\frac {s}{K}=S,\frac {t}{K}=Tとして、$$
$$\vec {OX}=s\vec {OA}+t\vec {OB}=S \vec {OA'}+T\vec {OB'}$$
$$さらにS+T=\frac {s}{K}+\frac {t}{K}=\frac {s+t}{K}=\frac {K}{K}=1$$
<考え方>
途中の式変形はs+tをKとおいて、
Kで両辺を割ることで(係数の和が1)のカタチになるように工夫しています。(但しK≠0)
はじめの条件から、0≦s +t=K≦3/2だったので、K=1ならば例題1と同じ線分AB
(ここでは、s≧0,t≧0の条件があるので直線ではなく線分です!)
を表します。が、不等式が入っているために一気に難しく感じる人が多いです。
条件の不等式が理解しにくい人へ
係数の和Kが0≦K≦3/2なので少し難しく感じるかもしれません、
そういう場合には上で書いたように、まずK=1の時を考えてみて下さい。
この場合は線分ABをあらわします。
次にK=0.5のときを考えると、OAの中点とOBの中点間の線分をあらわします。
ここで、もう一度条件の式をみると、0≦K≦3/2
なので、K=1の線分がK=0.8、0.7・・・となるに連れてOに近づき、K=0で点Oを意味します。
つまり、(あくまでも感覚的にですが、)
0≦K≦3/2の意味は、K=1.5,1.4,、、、0.5,0.4,0.3,0,2・・・、0の
それぞれの時の線分を全て足し合わせた結果、図示した領域の様になると考えると、
少しは理解しやすいのではないでしょうか。
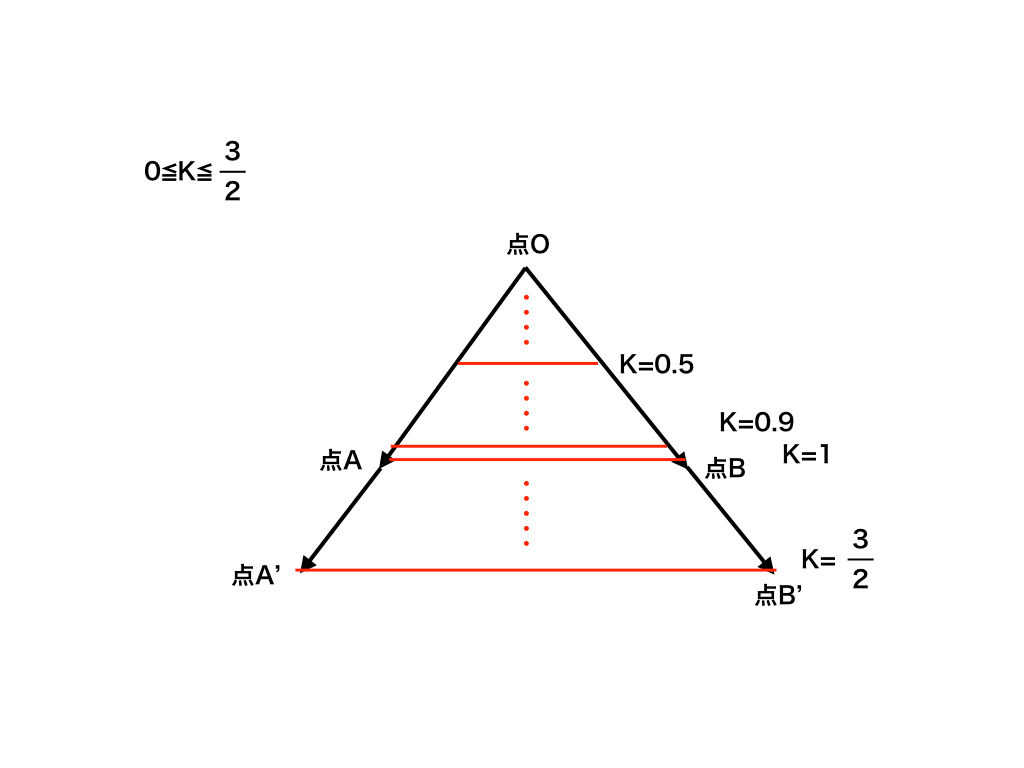
(実際には無数のベクトルの終点の集合です、、)
面積を求める問題:終点の存在範囲の応用
存在範囲を少し応用して面積を求める問題です。
問題2-2は(2-1)さえ解ければ、かなり簡単に解けるはずです。
三角形OAB=1として、OA’=3/2OA、OB‘=3/2OB より、図示した領域の面積は
9/4・・・(答)
まとめとベクトルの関連記事へ
このように、各ベクトルの係数の条件が不等式になることで、
ベクトルの先が通過する場所が線分から直線、領域に広がることがわかります。
とはいえ、基本はやはり”係数和1の法則”です。
それをもとにして、今回の問題の様にうまく変形する”コツ”がつかめれば、
終点の存在範囲のほとんどの問題は工夫して解くことが出来るようになります。
ぜひ、問題集や過去問から類題を探して練習してみてください。
↓ベクトルを得点源にするための記事をまとめました↓
今回も最後までご覧下さり、有難うございました。
当サイト「スマホで学ぶサイト、スマナビング!」は皆さんのご意見や、
記事のリクエスト、SNSでの反応などをもとに日々改善、記事の追加、更新を行なっています。
リクエストやご質問・ご意見がございましたらコメント欄にお寄せください。
また、B!や、いいね!シェア、Twitterのフォローをしていただけると助かります。
・その他のご依頼などに関しましては、お問い合わせページよりお願い致します。

