
平面・球面の方程式第3回「接平面とその周辺」
この記事では、空間ベクトル分野から【球面の方程式の応用問題】の解き方を解説していきます。
・球面の方程式、平面の方程式の作り方はだいたい理解できた人
を対象に、
・実際にどのような問題が出され、解いていくのかをstep by stepで紹介していきます。
目次(タップした所へ飛びます)
空間中で球面の方程式を使う応用問題
<※この記事は、「球面の方程式の求め方の解説」を前提に解説していくので、まだ読んでいない方は、ぜひ先に上のリンクよりご覧ください。>
2つの球が交わった時にできる円の方程式
さて、球面の方程式の応用問題で最も一般的なものから解いていきましょう。
空間座標中に球体が2つ存在しそれらが交わるとき、
その交わった面(円になります。詳しくは以下の図1参照)の方程式を問われる問題です。
<球体どうしの重なりのイメージ>
実際に問題を解きながら、理解していきましょう。
交わった円の方程式を求める
問題1:いま、xyz座標に中心点\(C_{A}=(1,-2,0),半径R_{A}=5\)の球体Aと、中心点\(C_{B}=(5,5,4),半径R_{B}=2\sqrt {13}\)の球体Bが存在する。この球ABが交わったとき、できる円の方程式を求めよ。
【解き方:二次元で考え、三平方の定理を利用する。】
下の図のように、いったん球A,Bの中心点を通る平面の図を描きます。
そして、球の中心間距離(空間中の2点間の距離の公式でも止めます)と、
球A,Bの半径より交わった断面の円の半径(下図では”r”の部分)を三平方の定理より導きます。
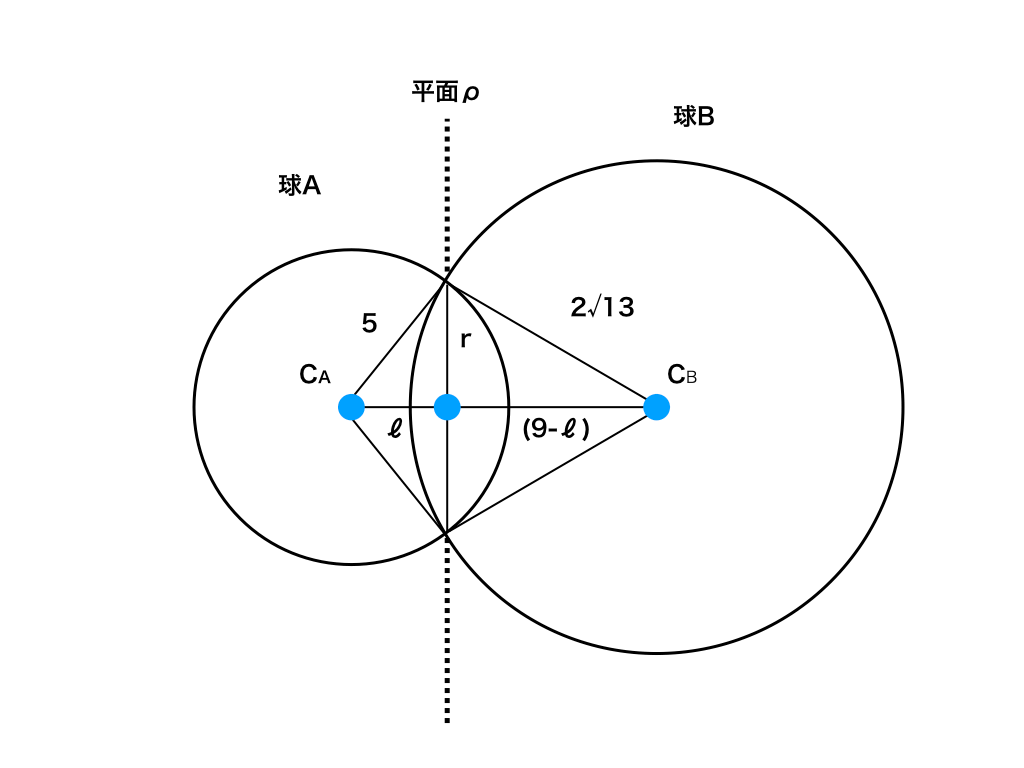
<球面同士が重なっている部分の断面図>
\(|C_{A}C_{B}|は、 \sqrt {(5-1)^{2}+(5-(-2))^{2}+(4-0)^{2}}=9\)
円の半径rと、CAから円の中心点までの距離をℓとすると、CBから円の中心点までの距離は(9-ℓ)。
三平方の定理より、\(5^{2}=r^{2}+ℓ^{2}と(2\sqrt {13})^{2}=r^{2}+(9-ℓ)^{2}\)
の2式を立てて、連立方程式を解く(r2とℓ2を消すのがコツです)と
ℓ=3,したがってr≧0よりr=4となります。(これで球同士が交わった切り口の円の半径rが求まった)
さらに、その円の中心点は\(C_{A}とC_{B}\)間を【ℓ:(9-ℓ)=3:6=1:2】
に内分したものなので、内分点の公式より
$$円の中心点=(\begin{pmatrix}
\frac {2+5}{1+2} \\
\frac {-4+5}{1+2} \\
\frac {4}{1+2}
\end{pmatrix})=(\begin{pmatrix}
\frac {7}{3} \\
\frac {1}{3} \\
\frac {4}{3}
\end{pmatrix})$$
ゆえに、円の方程式は、$$(x-\frac {7}{3})^{2}+(y-\frac {1}{3})^{2}+(z-\frac {4}{3})^{2}=16 \ldots (答)$$
円が存在する平面の方程式を求める
次は、問1の少しだけ発展させた問題です。
具体的には、断面(円)が存在する平面の方程式を求める問題です。
問題2:いま平面ρ上に(問1)で求めた円が存在する。この平面ρの方程式を求めよ。
こちらも、どの様な平面を求めるのか先に図を見ておきましょう。

<球体と球体の平面ρのイメージ図>
※:この(問題2)と次の(問題3)は、「平面の方程式と法線ベクトル」で紹介した法線ベクトルを使います。
上のイメージ図の球と球の間に描かれた平面がこの問題で求める平面ρです。
断面の部分がよく見ると円(問1で求めた円)になっているのがわかると思います。
この平面ρの方程式を求める方法はいくつかありますが、
最も簡潔な「法線ベクトルと1点」がわかっていれば導ける方法を使います。
(この解法について詳しくは、上のリンクを参考にしてください)
さて、簡単に復習すると平面ρの方程式は1点と、
その点を通る法線ベクトル\(\vec{n}\)が定まれば求まるので、法線ベクトルを探します。
この場合、球A,球Bの中心点を結ぶベクトル \(\overrightarrow{C_{A}C_{B}}\)は平面ρに垂直です!
したがって\(\vec{n}=\overrightarrow{C_{A}C_{B}}=(4,7,4)\)
さらに、$$\vec{n}は円の中心(\begin{pmatrix}
\frac {7}{3} \\
\frac {1}{3} \\
\frac {4}{3}
\end{pmatrix})$$を通るので、
法線ベクトルの成分と平面の方程式の係数の関係から、4x+7y+4z+d=0。
これに円の中心座標を代入すると、
$$4×\frac {7}{3} +7 ×\frac{1}{3} +4×\frac{4}{3}+d=0$$
分母の3を払って整理すると、51+3d=0。よってd=-17
より、平面ρの方程式は:4x+7y+4z=17・・・(答)
球と平面が接する(接平面)の方程式を求める
今度は球の「接平面」を求める問題です。
2直線が接する点が「接点」、接する線が「接線」であったように球に接する面を「接平面」と言います。
この問題も法線ベクトルで簡単に解けるので、ぜひマスターしておきたいところです。
(問3)方程式(x-1)2+(y-3)2+(z+1)2=45であらわされる球が、接点T(5,5,4)で平面πと接する時、
その平面πの方程式を求めよ。

<球と接平面のイメージ図>
<解答解説>
まず接点Tへ球の中心から下ろした線分CTは、平面πと垂直になります。
したがって、球の中心を点Cとすると、\(\overrightarrow {CT} ⊥平面π より\)
\(\overrightarrow {CT}\)が平面πの法線ベクトル\( \vec {m}\)となります。
\(\overrightarrow {CT}\)を成分表示すると、(5-1.5-3.4-(-1))
\(\vec {m}=(4,2,5)\) ここで法線ベクトルの成分が平面πの方程式の係数になることを利用して、
4x+2y+5z+d=0 が求める平面πの方程式です。
さらに、接点Tは平面π上にあるので、上の式にT(5,5,4)を代入して、
20+10+20+d=0 よってd=-50
(∴)4x+2y+5z-50=0 ・・・(答)が接平面の方程式となります。
まとめと空間ベクトルの方程式シリーズ一覧
・球と球が交わった面には円ができ、三平方の定理の利用を考える
・接平面や、断面の方程式は「法線ベクトル」を積極的に使う
次回は、法線ベクトルとその応用について解説します(2018/12/28現在作成中)
【数B】平面・球面の方程式シリーズ【空間ベクトル応用】
第一回:「平面の方程式と法線ベクトルの使い方」
第二回:「球面の方程式の求め方と例題」
第三回:「今ここです」
第四回:「(作成中)」
【知識0から】ベクトルシリーズまとめ【最難関大レベルまで】
この記事が役に立ちましたら、B!やいいね!、等SNSでシェア&フォローをお願いします!
ご質問や記事のリクエストもお待ちしています。

