正射影ベクトルとは何か?どう役立つのか?
この記事は、ベクトルの基礎はわかってきたけれども、「正射影ベクトル」がよく分からない。
そんな人を対象に、正射影ベクトルをイラストを使ってわかりやすく解説したものです。
・正射影ベクトルの公式
・実際どんな問題で役立つのか
といった重要な点をまとめました。
(※:知識に抜けがあれば、→「ベクトルの解説記事総まとめ」のページから該当分野の記事を読んでからこの記事をご覧ください。)
目次(タップした所へ飛びます)
正射影ベクトルとは
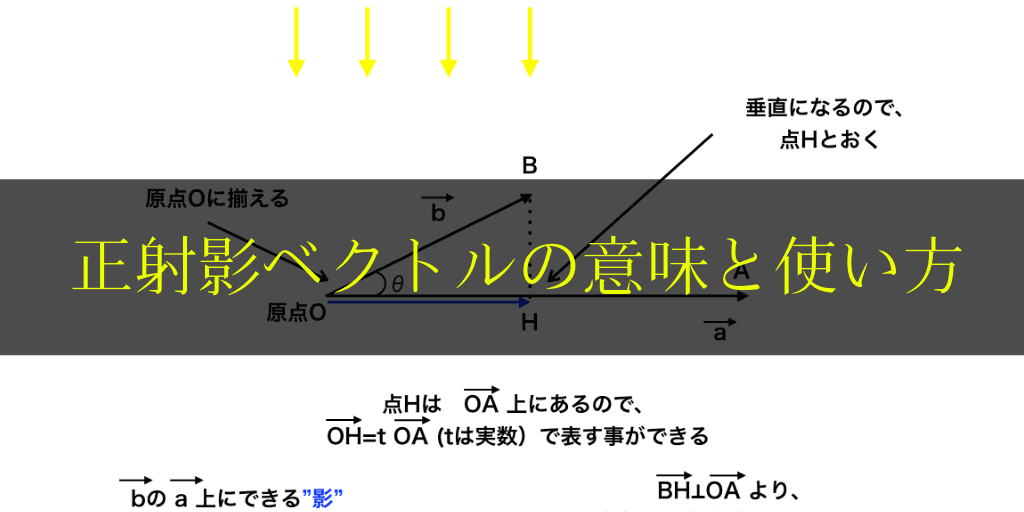
正射影ベクトルは、その名の通り「あるベクトルに光を真上から射(さ)した時の影となるベクトル」のことです。<以下の図参照>
正射影ベクトルの公式とその意味
まず視覚的に“正射影ベクトル”はどの様なものかわかってもらうために下の図をご覧下さい。
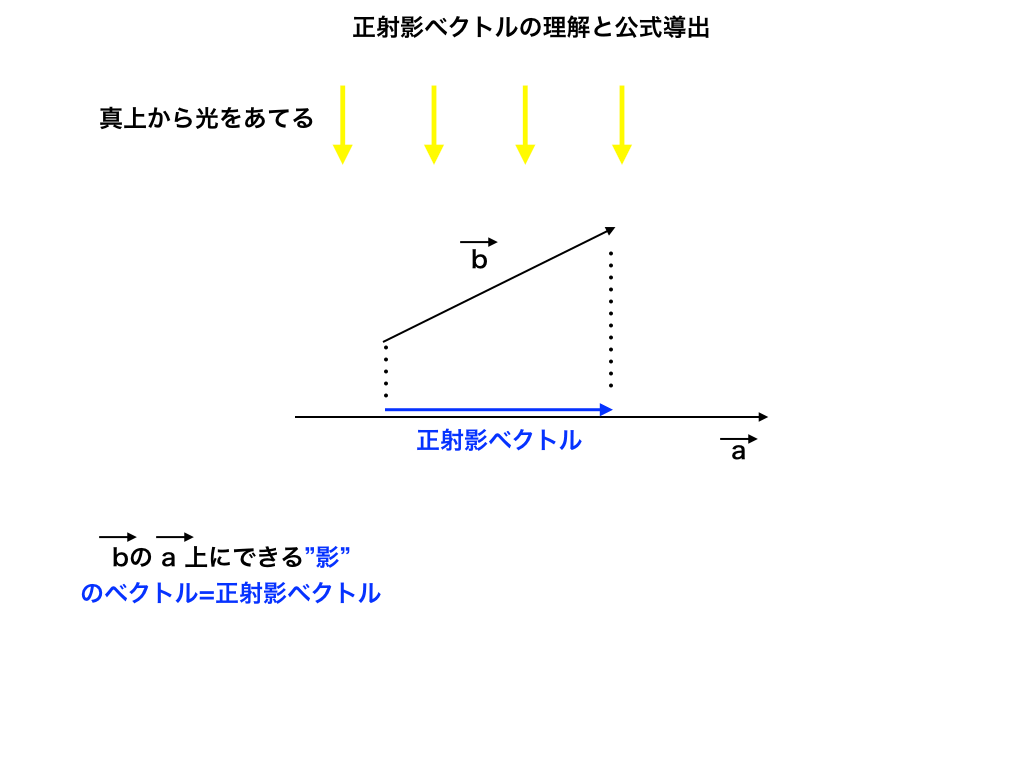
<正射影ベクトルのイメージ図>
青色のベクトルが、「aベクトルに対するbベクトルの正射影ベクトル」と言われます。
公式の導出
さて、以下のようにベクトルa,bがあり、bのaに対する正射影ベクトルは公式として、
正射影ベクトル→OH
\(\mathrm{\vec {OH}=\vec {b} \cdot \vec {e_{a}}}\)
\((ただし、\mathrm{\vec {e_{a}} は\vec {a}}の単位ベクトルとする)\)
で表すことができます。この項ではその公式の導出法を学びます。
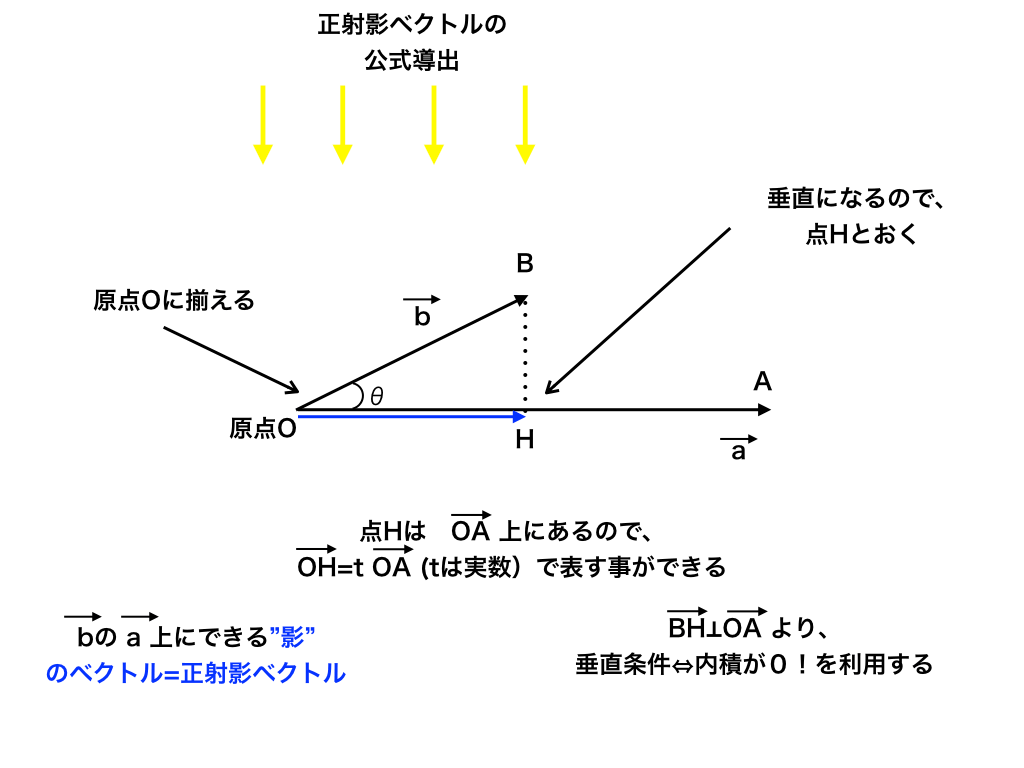
<正射影ベクトルの公式導出>
まず、ベクトルAとBの始点を揃えます。そしてベクトルBの先の影の部分(垂直に下ろしたところ)を点Hとします。
点Hは、ベクトルOA(以降\(\vec {a}\)とします)上にあるので、実数”k”(文字は何でも構いません)を使って、\(\vec {OH}=k\vec {a}\)と書けます。
次に、\(BH⊥\vec {a} \)より、内積を利用します。
(垂直⇔内積が0:<参考:「ベクトルの内積と垂直・平行条件」>)
この時、\(\mathrm{\overrightarrow{BH}を\overrightarrow{OH} }-\vec {b}\) に分解して、
\((\overrightarrow{OH} -\vec {b}) \cdot \vec{a}=0\)
,
\(\mathrm{\overrightarrow {OH}=k\vec {a}}\)と合わせて
\((k\vec {a}-\vec {b})\cdot \vec{a}=0\)
展開し、ベクトルの二乗は大きさになることに注意して
$$\mathrm{k|\vec {a}|^{2}-\vec{a} \cdot \vec{b}=0}、よって、\mathrm{k=\frac {\vec {a}\cdot \vec {b}}{|\vec {a}| ^{2}}}$$
\(\mathrm{\overrightarrow {OH}=\frac {\vec {a}\cdot \vec {b}}{|\vec {a}| ^{2}}\cdot \vec {a}}\)
\(\overrightarrow {OH}=\frac {|\vec {a}| \cdot \vec {b}}{| \vec {a}| ^{2}}\cdot \vec {a}\)
ここで、内積の定義より\(\mathrm{\vec{a} \cdot \vec{b}=|\vec {a}||\vec {b}|\cos θ}\)
\(|\vec {b}|\cos θ=|\overrightarrow {OH}| \)(上図参照)より、
正射影ベクトル\(\mathrm{\overrightarrow {OH}=|\overrightarrow {OH}|\cdot \frac {\vec {a}}{|\vec {a}|}}\)
正射影ベクトルはどんな問題に役立つのか?
以上の様にして正射影ベクトルの公式と意味を学びました。
わざわざ意味もなく求めているわけではなく、様々なベクトルの問題がスマートに解けるようになります。
さらに、【ベクトルの分野と一見何の関係も無さそうな分野でも】正射影ベクトルは威力を発揮します。
ここでは、そのうちの正射影ベクトルが役立つ代表的な問題を紹介し、解答では図形と方程式など他分野の考えを使って確認していきます。
正射影ベクトルを利用する問題例
問題:『<問題図1>のように、xy座標平面上にy=-xで表される直線と点A(1,3)がある。Aから直線に垂線を下ろしたとき、その足の点の座標を求めよ。』
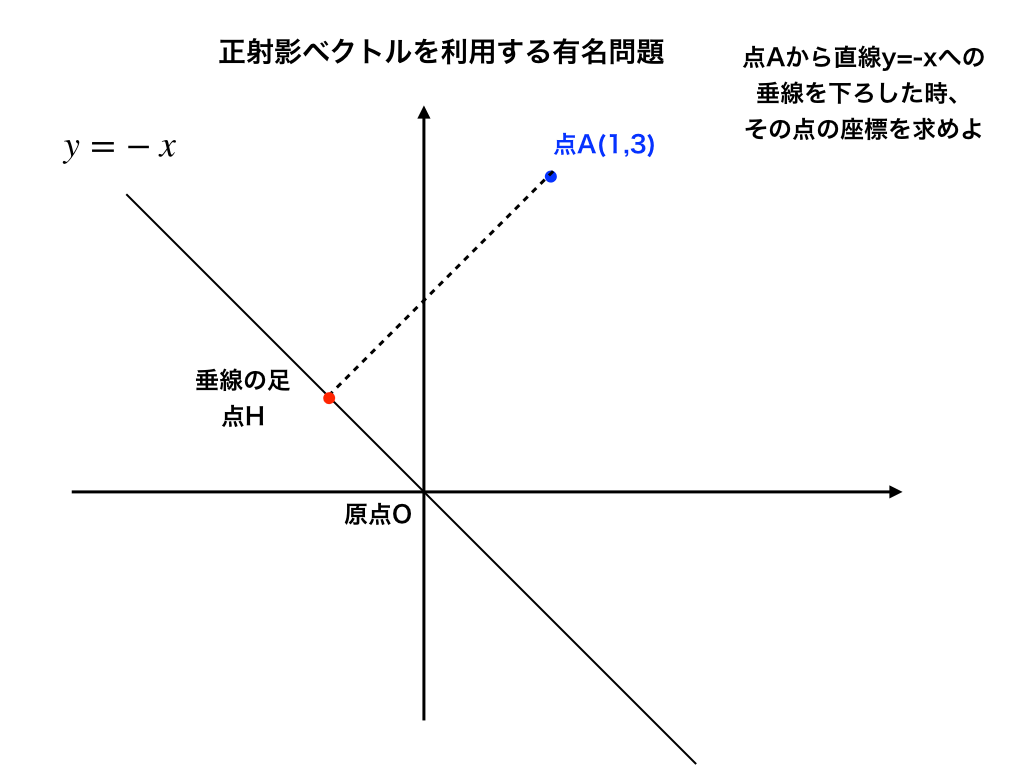
<問題図1>
解答の手順
この手の問題では、点Hの座標を求める=ベクトルOHとベクトルOAを考えます。すると、条件より∠AHO=90°なので、(下に続く)
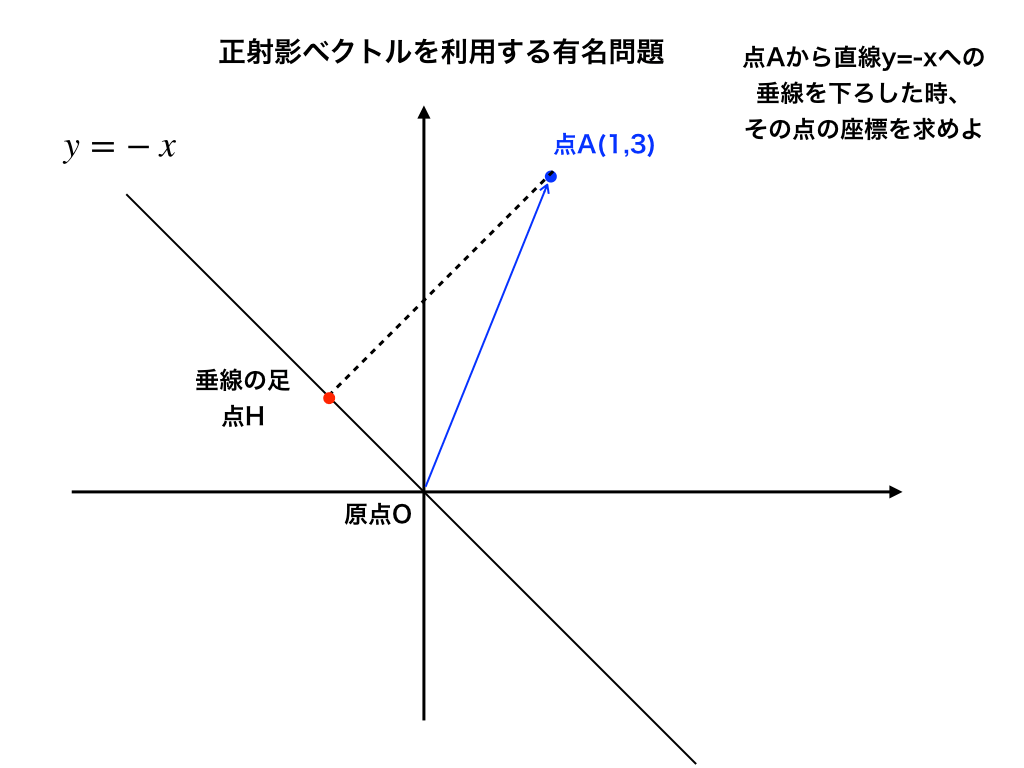
<解説図2>
ここで、ベクトルOAの”真上”から光が射し込んでいる状況を考えると<解説図3>
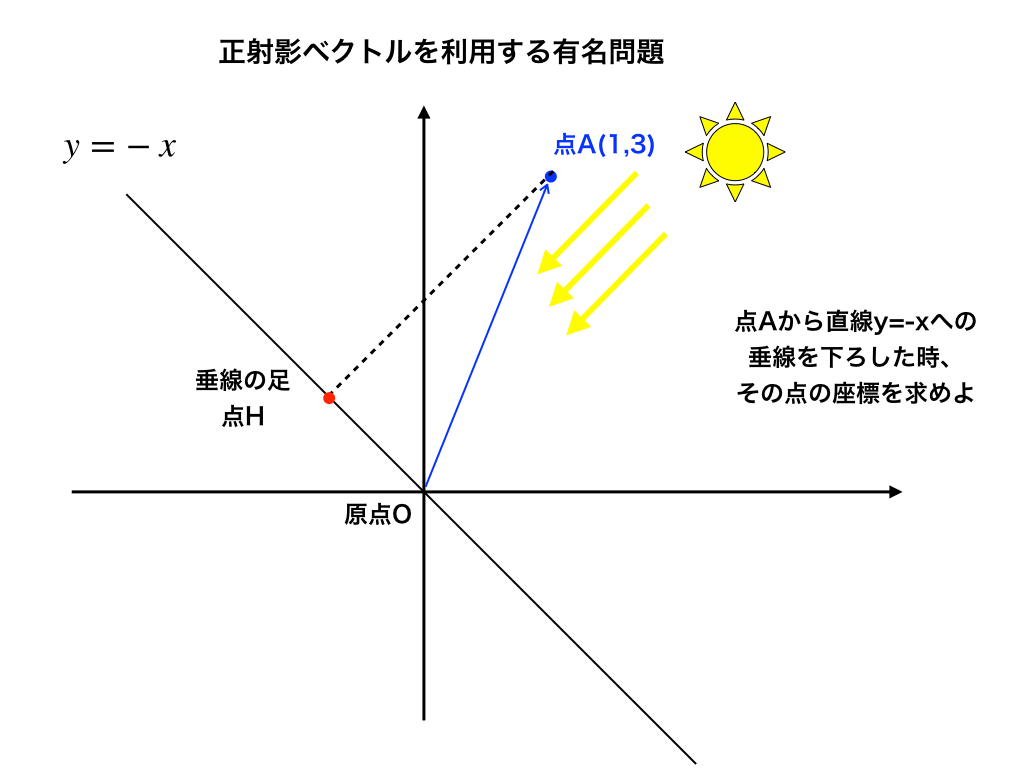
<解説図3>
このように、OHはベクトルOAの正射影となっている事がわかります。つまり、正射影ベクトルの出番です!
正射影ベクトルの式を思い出しながら、解答を作っていきます。
まず、直線の方向ベクトルをuとすると、
\(\vec {u}\begin{pmatrix}
1 \\
-1
\end{pmatrix}であり、\overrightarrow {OA}=\begin{pmatrix}
1 \\
3
\end{pmatrix}です\)
今ベクトルOHを求めたいので、
$$\overrightarrow {OH}=\frac {\vec {u}\cdot \overrightarrow {OA}}{\left| \vec {u}\right| ^{2}}\cdot \vec {u}$$より、
\(=\frac {\begin{pmatrix}
1 \\
-1
\end{pmatrix}\cdot \begin{pmatrix}
1 \\
3
\end{pmatrix}}{2}\cdot \begin{pmatrix}
1 \\
-1
\end{pmatrix}\)
内積を成分で計算して、(参考:「ベクトルの成分表示での計算・内積」)
\(=\frac {1-3}{2}\cdot \begin{pmatrix}
1 \\
-1
\end{pmatrix}=-1\begin{pmatrix}
1 \\
-1
\end{pmatrix}\)
したがって、点Hの座標は(-1,1)である事が求まりました。
座標上の距離で確認してみる
本当に点Hの座標が(-1,1)なのか、三平方の定理で確かめてみましょう。
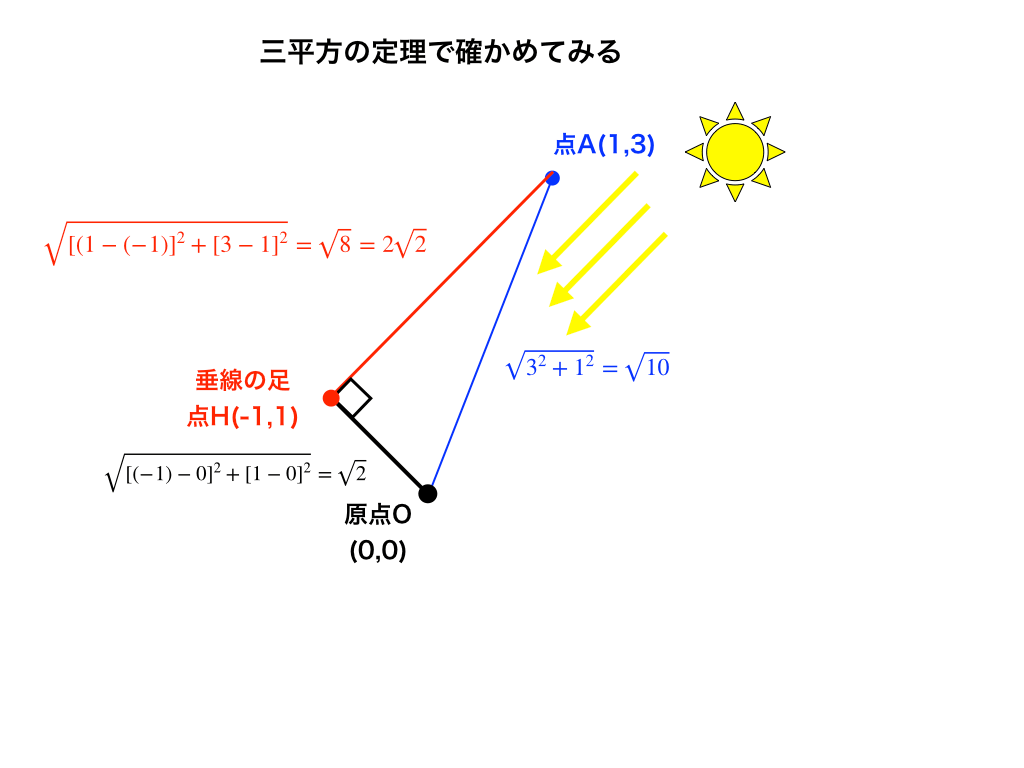
上の図の様に、距離AO=√10,AH=2√2、そして距離OH=√2と求まります。
次に、三平方(ピタゴラスの定理)より、\(\mathrm{OH⊥AHだからOH^{2}+AH^{2}}=2+8=10\)
従って、\(OA^{2}=10,\sqrt{10}\)と計算でき、確かに先ほどのHの座標が正しいことがわかりました。
まとめとベクトルの関連記事紹介
・正射影ベクトルの公式は『覚えず』に、面倒でも一回一回導きましょう。(その過程で、自然に覚えてしまいます)
・今回は応用問題1題を紹介しましたが、正射影が使える問題や分野はかなり多いので問題集や過去問を解く際に『ベクトル』を使えないかを常に頭に置いておきましょう。
<<「ベクトルを0から難関大入試まで攻略するの記事総まとめ」>>
・空間図形でも(正射影を含む)ベクトルは大活躍します。
空間ベクトルの応用シリーズ
第一回:「平面の方程式の求め方と法線ベクトル」
第二回:「球面のベクトル方程式と基本問題」
第三回:「球と球が重なった時にできる円や平面の方程式」
第四回:「法線ベクトルの求め方と空間図形の問題への応用」

