
物理基礎で挫折しない為の三角比・ベクトル講座
学校のカリキュラムによっては、数学1(三角比)や数学B(ベクトル)を学ぶ前に、物理基礎の力学を学ぶ事があります。
そう言った場合、物理基礎の始めに習う「速度の分解・合成」や「力の分解・合成・釣り合い」が理解し辛い場合があります。
この記事ではそう言った人が物理基礎で挫折しないように、以下の事を簡単に説明します。
この記事で学べる事
・まずどの様な問題で三角比やベクトルが必要になるのか紹介します。
次に、
・三角比(sin・cos・tanの意味・計算とその周辺)
・ベクトルの意味と足し算
・上二つの少し応用
をそれぞれ必要な所に絞って解説します。
そして、最後に
・一番最初に挙げた、三角比とベクトルを使った物理基礎の確認問題を二題解きます。
目次(タップした所へ飛びます)
物理基礎で三角比やベクトルが必要な例題
具体的な問題を見ていきます。
川を渡る船の速さと向き
下の様な<図>と共に、「今川が右向きに√3(m/s)で流れている。
その流れと垂直に、船が対岸に渡ろうと1(m/s)で進んだ時、船は〇方向へ〇m/sで進む。」
(〇の部分を回答する)と言った問題が出されます。
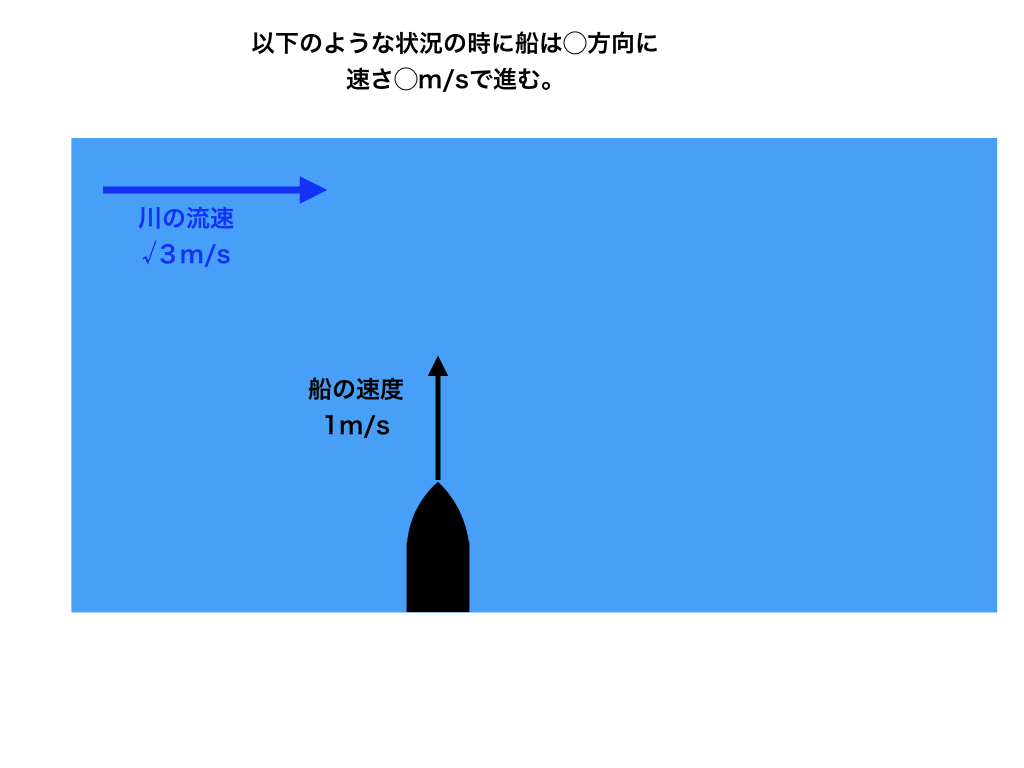
<図1:川を渡る船の速度の合成>
固定された台上にある物体の重力の分解
他にもベクトル・三角比が関係する問題があり、この問題は「力」の分解です。
<図2>の様な三角台Aの上に質量mの物体が乗っている。
三角台Aは固定されており、重力加速度をgとする。この時の台からの垂直抗力Nと斜面に沿った物体の力を求めよ。
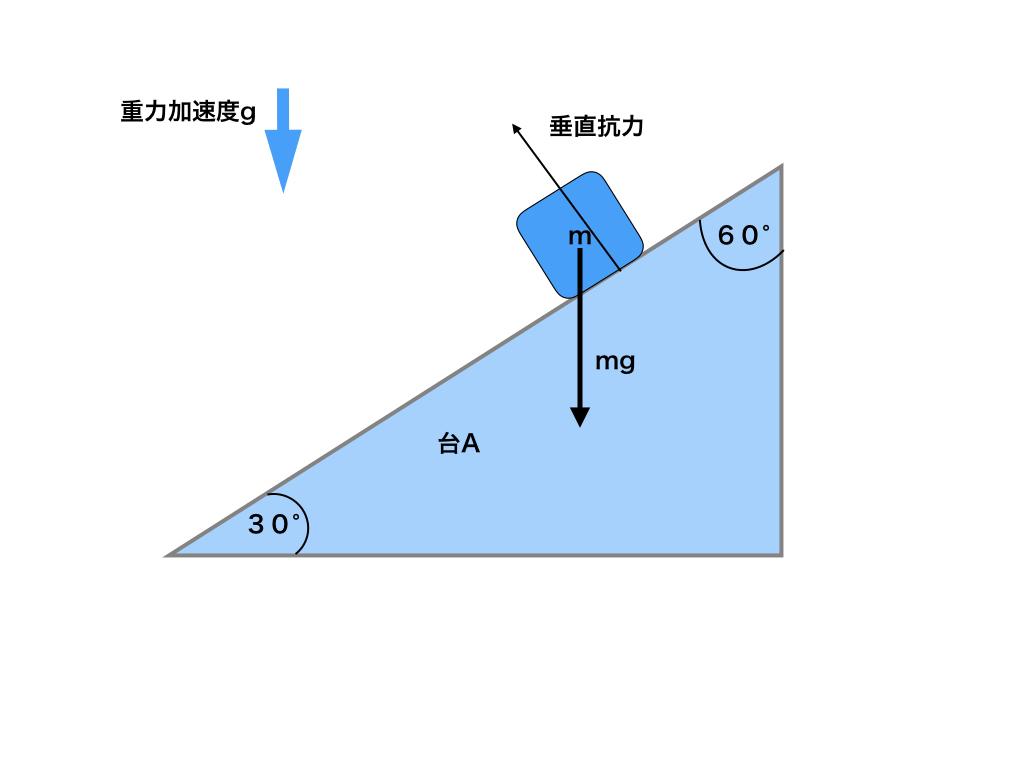
<図2:三角台上の物体の重力とその分解>
三角比とベクトルの基礎を解説
この項では三角比の基本を紹介しています。
さらに詳しくは→「三角比の表と正弦定理・余弦定理・面積公式を1記事で解説」をご覧ください。
三角比とは
三角比とは、いわゆる「サイン(正弦:sin)・コサイン(余弦:cos)・タンジェント(正接:tan)」と言うものです。
「三角形の辺の長さの比」と考えて下さい。
名前は難しく感じるかもしれませんが、筆記体のsとcとtが書ければ、あとは自然と慣れてきます。
三角比での有名三角形
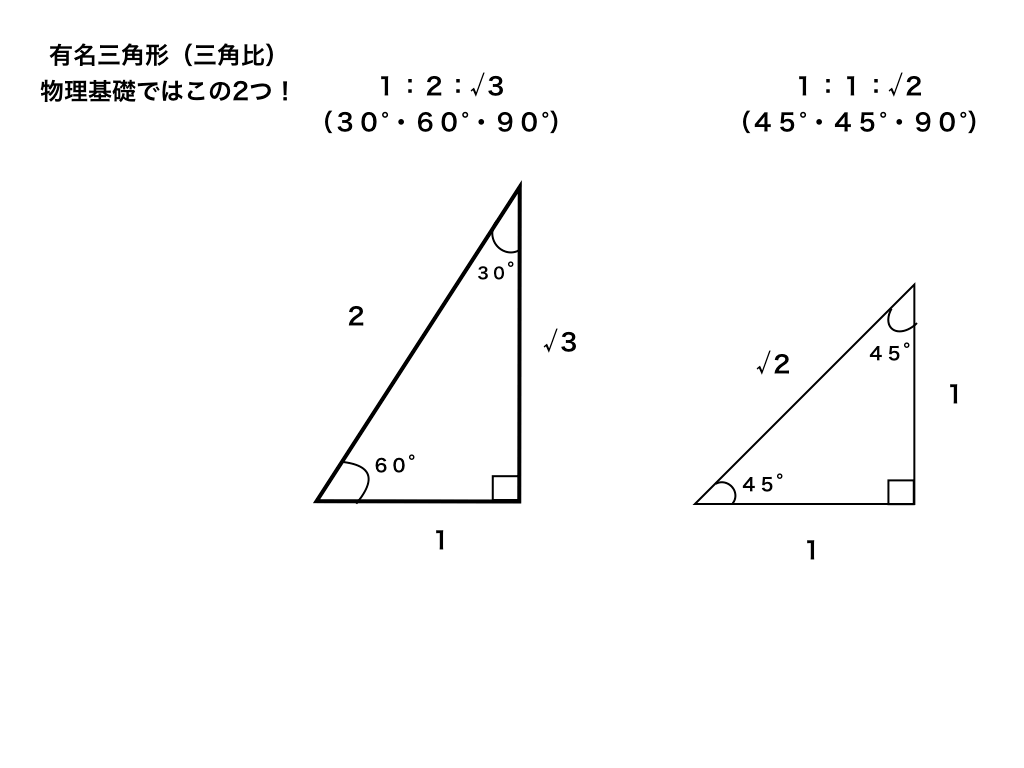
まずはこの2つの有名三角形を覚えましょう。
三角比を発展させた三角関数(数2)以降でも、とにかく良く利用します。
\(辺の比が1:2:\sqrt{3}\)で
角度が90°、60°、30°の左側にある三角形と
\(辺の比が1:1:\sqrt{2}\)で
角度が90°、45°、45°の直角二等辺三角形です。
sin・cos・tanの簡単な求め方
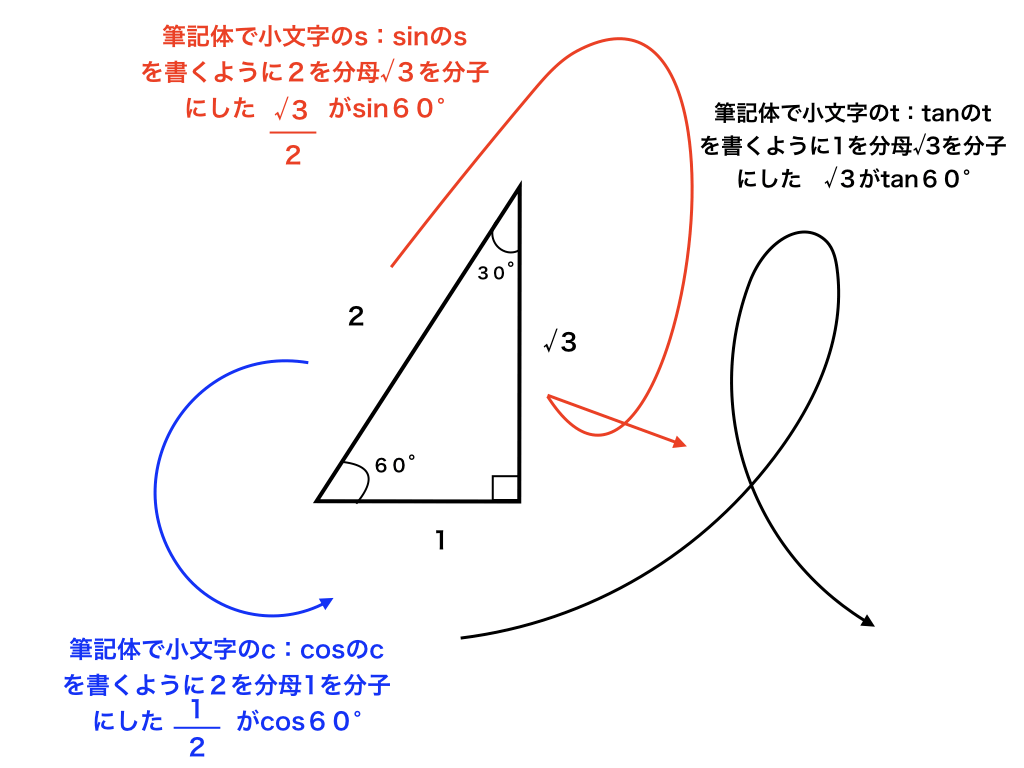
上の図参照:
筆記体のsを書くように90°の対辺2分の√3がsin60°。
筆記体のcを書くように、分母を2、分子を1にしたものがcos60°。
tを書くように、1分の√3=√3にしたものがtan60°です。
では、cos30°はいくつでしょうか?
自分で三角形を描いて考えてみてください。
・・・
・・・
$$答えは「\frac{\sqrt{3}}{2} です。$$
解けたでしょうか?一応解説の図を下に載せます。
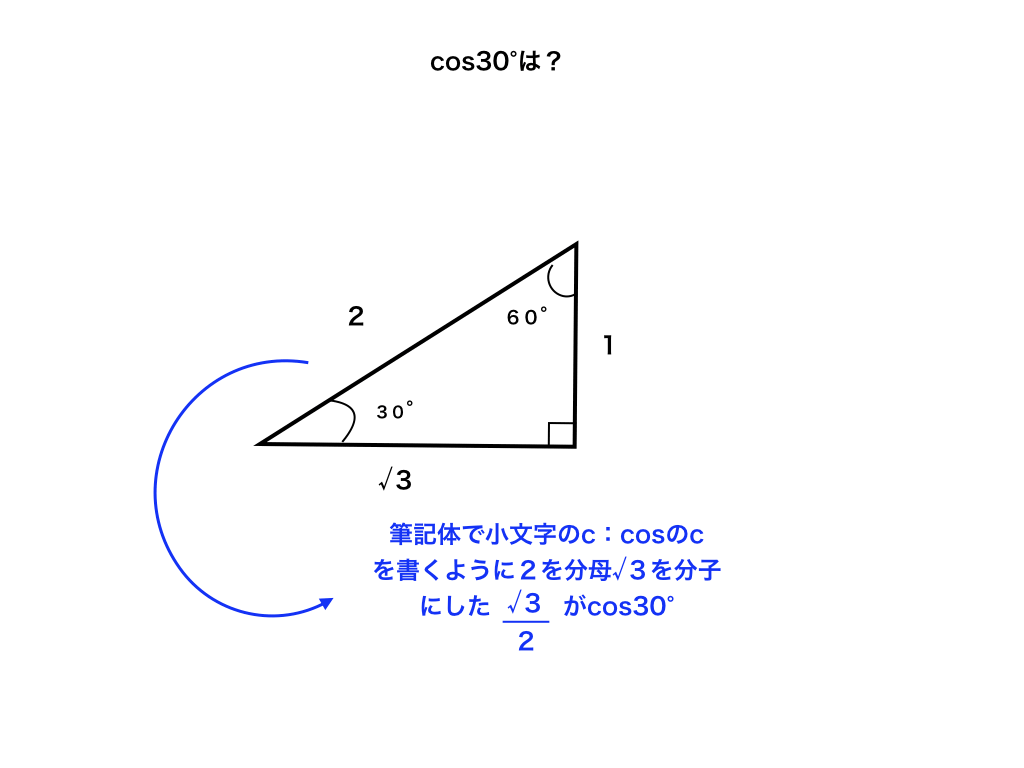
<解説図>
今度はcos30°なので直角を右下・30°を先程の60°の位置に持ってきて、筆記体のcを書きます。
すると、\(\frac{\sqrt{3}}{2}\)、2(分母)分の√3(分子)となります。
三角比・三角関数についてさらに詳しくは→「三角関数・三角比の公式を覚えない方法」をご覧下さい!
ベクトルの基礎
物理基礎では、数学Bのベクトルで学ぶほど深い知識は必要ありません。
「スカラー量」と「ベクトル量」の違い・ベクトルの足し算・引き算の基礎がわかれば十分です。
詳しくは、「ベクトルとは?0から学ぶ記事9選」に書いていますが、その一部を紹介します。
ベクトルとは、「向き」と「大きさ」という二つの「情報」を持っている矢印のことです。
それに対して、これまで我々が扱ってきた「数」という一つの情報しか持っていないものを「スカラー」と言います。
これだけでは?な人もいると思うので、筆者が良く使う例え話をします。
Aさんは友人のB君の家へ行くためにB君の家の最寄りの駅に到着しました。
ココから家へ向かう為にB君が教えてくれたのは、「駅から300m歩いたところに僕の家があるよ!」でした。
この伝え方には「300m」という一つの情報しか含まれていません=(スカラー量)。
従って駅から半径300mの円周上を歩いて探さなければいけません。
対して、「駅から真東に300mのところが僕の家だよ。」と教えてくれたとしたらどうでしょう?
「方向=真東」、「距離=300m」の二つの情報が含まれている(=ベクトル量)ので、AさんはピンポイントでB君の家へ向かう事ができます。
この違いがベクトルの理解への第一歩です。 <当サイト内記事:「ベクトルとは?0からわかる記事9選」より。>
要するに、「大きさ」だけ持っているのが「スカラー量」で、
「向き」も合わせて持っているものが「ベクトル量」というわけです。
そして、物理においてはそのベクトルの「分解」や「合成」が最重要pointです。
ベクトルの合成(足し算)
これは図を見た方が早いので↓をご覧下さい。
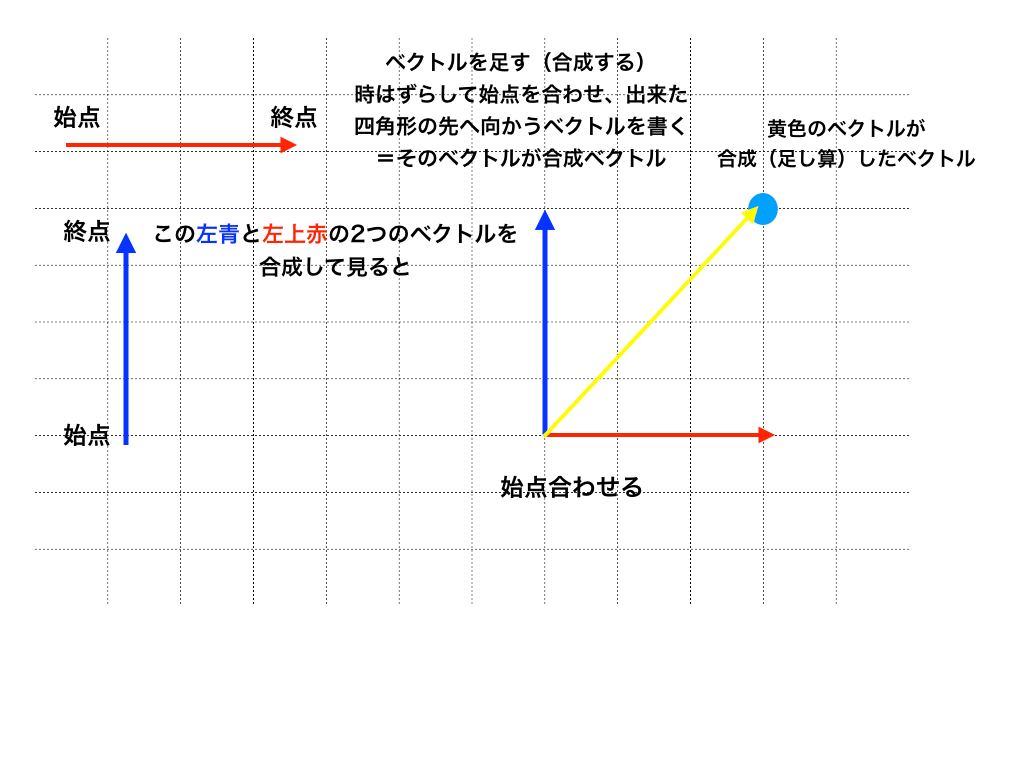
<ベクトルの合成図>
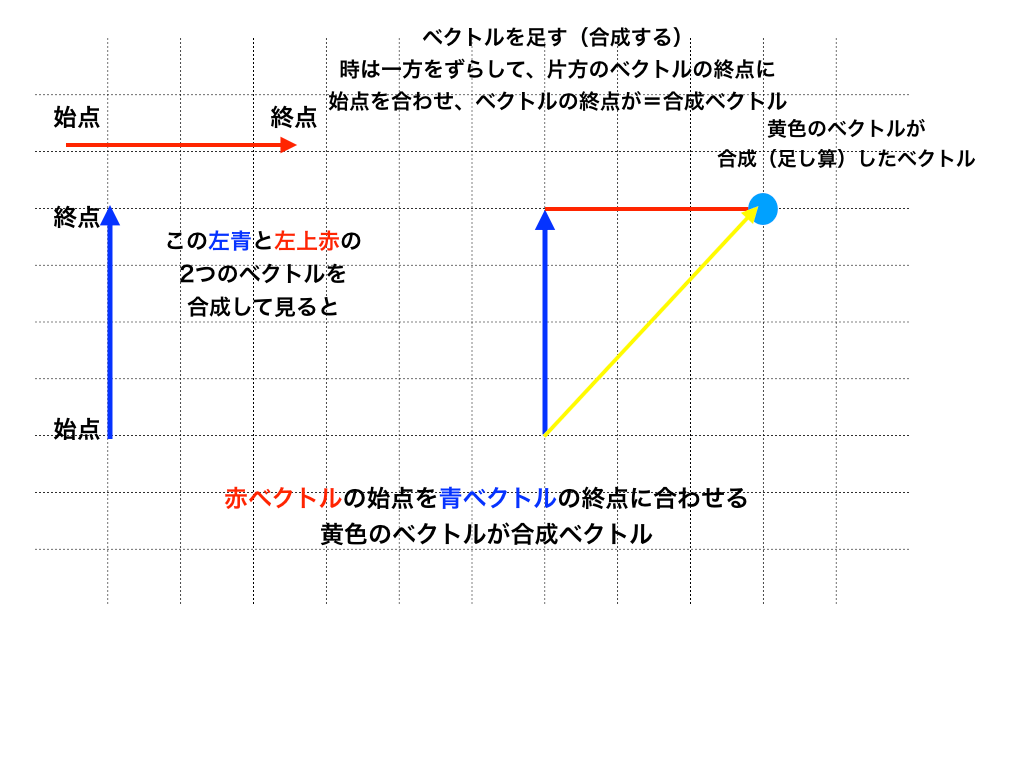
ベクトルの足し算を二つの図で解説していますが、どちらの方法でも同じ結果(黄色のベクトル)になります。
2つの例題の解答解説
最初に紹介した、力の分解と船の速さの問題を今回学んだ数学の知識を使って解いていきましょう。
船の速さの問題
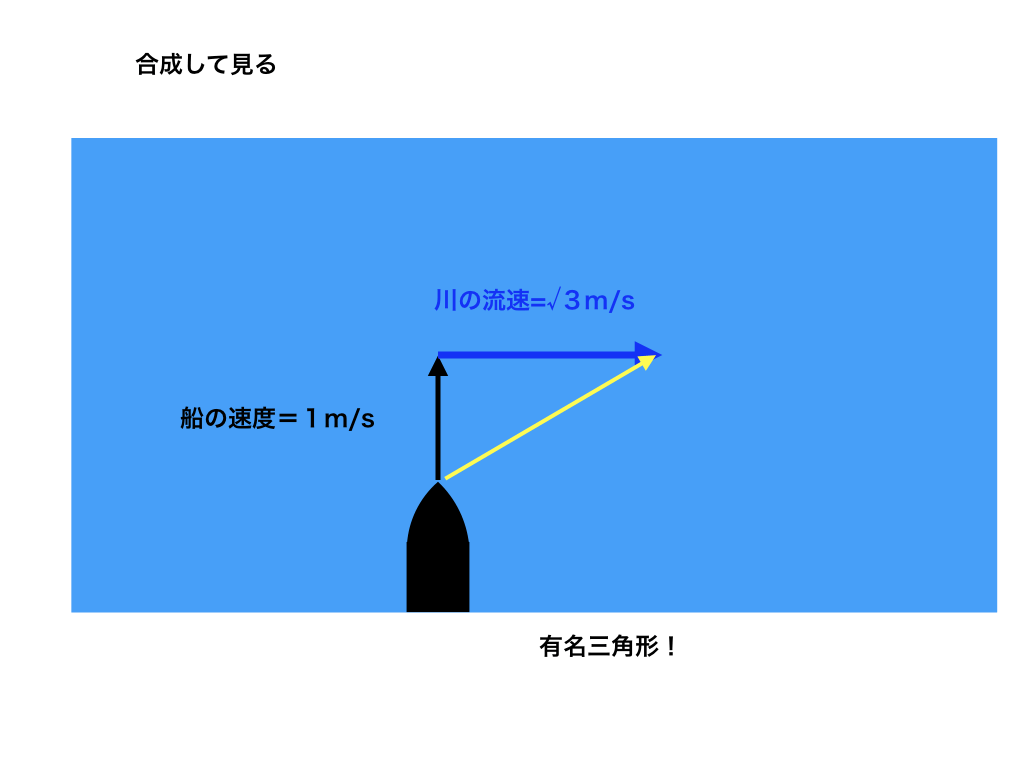
上で学んだ”ベクトルの足し算”と”三角比”を使うことを考えて、
問題は『どの方向へ何(m/s)で船が進むか?』だったので、ベクトルの足し算を行います。
黒のベクトルと青のベクトルを足し算したものは、黄色のベクトルになります。
更に、辺の長さが\(1:\sqrt{3}\)になっているので、これは\(1:2:\sqrt{3}\)の有名三角形です!
従って、答えは、(川の流れと垂直な黒のベクトルより)時計回りで、60°の方向に2(m/s)で進む。
力の分解の問題
この問題は台Aと台上の物体(質量m)に働く「垂直抗力N」と台の斜面に水平な力を求めるものです。
この様な問題では、物体にかかる重力=mgを、
それぞれ三角台の斜面に水平な方向と、斜面に垂直方向へ分解します。
物体が斜面垂直下向きにかかる力=垂直抗力
斜面水平にかかる力=斜面をすべり降りる力になります。
(運動方程式につながるので、未習の人は飛ばしても構いません。)
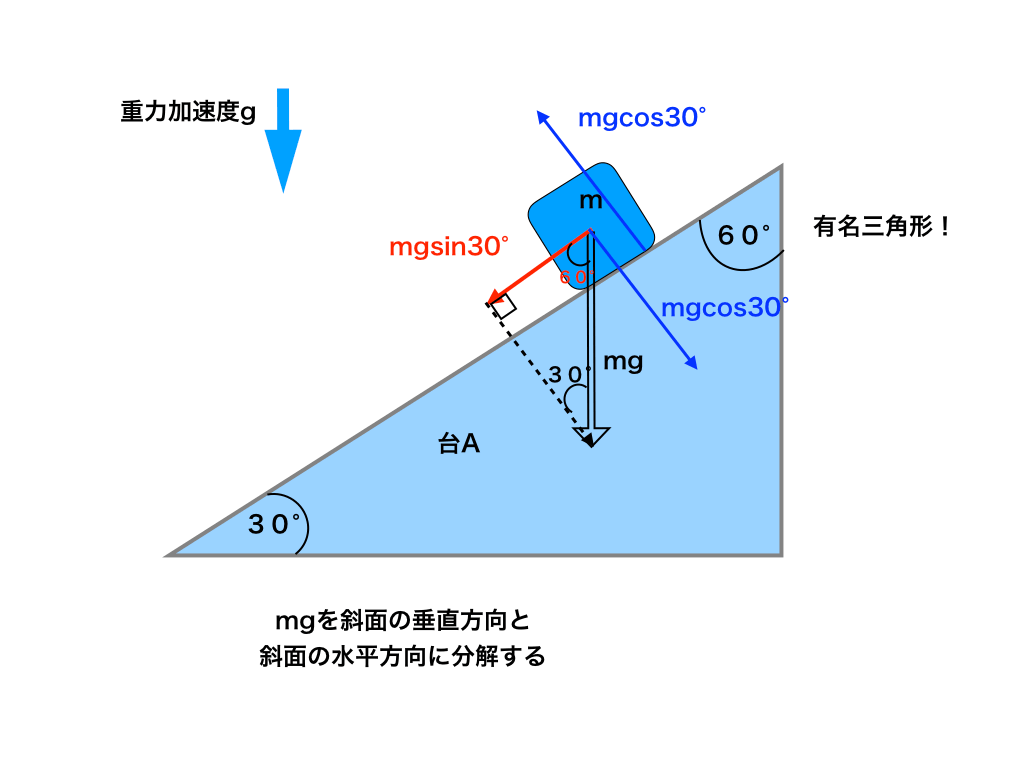
<図:三角台上の物体の重力を分解>
上図のように、mgを「分解」しています。
これは、先ほどのベクトルの合成の逆を行なっています。
重力を斜面水平・垂直の二つの方向に分けたベクトル(赤ベクトルと青ベクトル)であらわして、錯角などを利用し、角度を求めます。
最後に、三角比を用いて求める垂直抗力N=mgcos30°、斜面に水平な力F=mg sin30° として終了です。
$$答えは:N=\frac{\sqrt{3}mg}{2}$$
$$F=\frac{mg}{2}$$
まとめと応用記事へのリンク
さあ、これで物理基礎で必要な数学の知識はバッチリです!
あとはこれを身につけて応用していくのみです。
物理は初めは取っ付きにくく、早くにあきらめてしまう人が多い科目ですが、一度理解出来れば大変面白い科目でもあります。
また、試験においても安定して高得点を狙っていけるので、1人でも多くの人が興味を持つキッカケになれば幸いです。
>>「力学が苦手な人〜難関大レベルまでの”解説記事総まとめ!”」<<
応用記事:鉛直投げ上げ・斜方投射へ
このサイトは皆さんのご意見や、記事リクエスト、SNSでの反応などをもとに日々改善・記事追加更新を行なっています。
・記事リクエストと質問・ご意見はコメント欄にお寄せください。可能な限り対応します。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼はお問い合わせページよりお願い致します。

