
最短経路の問題(場合の数と確率シリーズ)
<この記事の内容>:碁盤の目のようになった道を【最短(後戻りしたりせず)で目的の点まで行く場合の数】を求める”頻出問題”の解き方を例題・イラストとともに紹介しています。
<参考:これまでのシリーズ>:「場合の数と確率分野の公式・解法総まとめ」も必要に応じてご覧ください。
応用編「ランダムウォークと確率の問題」を作成しました!この記事を読み終わったら、ぜひ続けてご覧下さい。
目次(タップした所へ飛びます)
最短経路の問題とは
上述の通りなのですが、実際に例を使って解説していきます。
例題1:次の<図1>の道をAからBに最短で(戻ることなく)行く方法は何通りあるか。

最短経路の問題の解法1「書き込む」
さて、最も基本的な解き方は『図上に(場合の数を)書き込むという方法です』。
この方法を正式名称ではありませんが、「書き込み法」という名前で呼ぶこととします。
具体的には、次のように
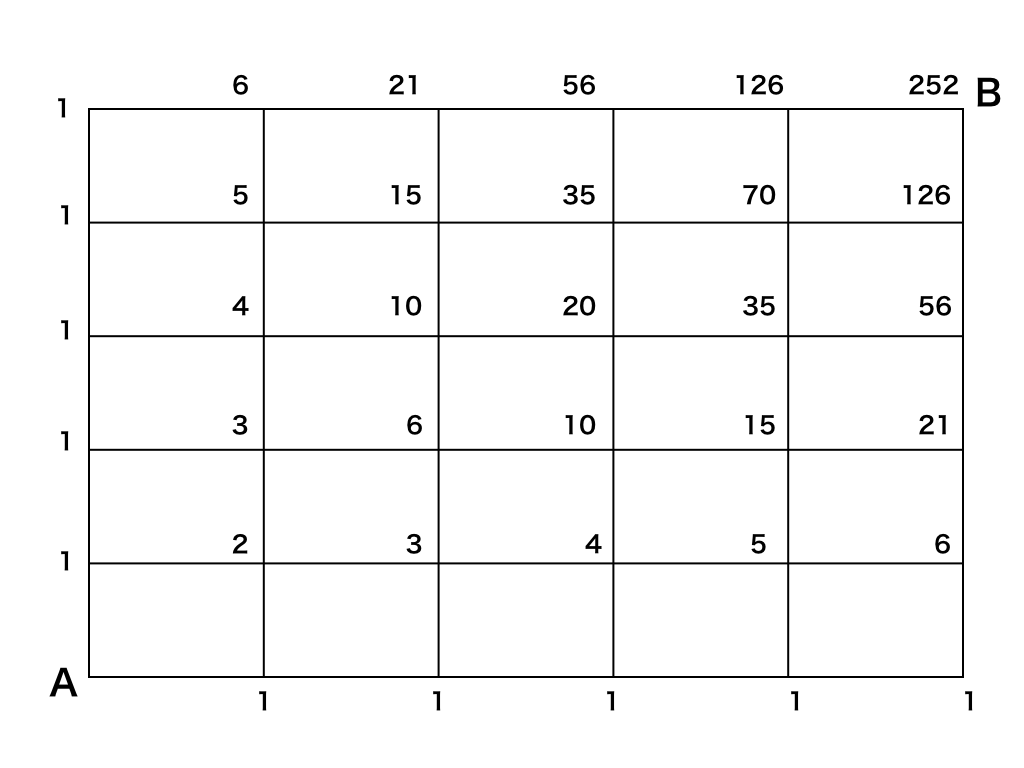
Aから上方向に1,1,1・・と、右方向に1,1,1・・・と書き込みます。(これは例えばAから2番目・3番目・・・5番目の上の点まで進む”最短経路はそれぞれ1通りしかない”という意味です。
Aから右方向の2番目・・・5番目までの最短経路も1通りしかありません。(ただ右向きに進むしかないからです)
次に、各マスの右下の数字と左上の数字を足し合わせて右上に書きます。(1+1=2、2+1=3・・・といった具合です)
これは、右上の位置に最短で到達する場合の数を計算しています。
Aの右上の『2』ならば、"右へ1回進んで上に進む"か/"上に1回進んで右へ進む"かの2通りしかありません。この数字は確かに(右下)+(左上)=2と一致します。
この計算をすべてのマス目で行なっていきます。
すると、上の図のように『252(通り)』の道順があることが計算できます。
解法2「同じもの(数)を並べる順列」を応用する
上の図に直接書き込む方法は、マス目の数が非常に大きくなったりした場合には使い勝手が悪いです。
計算に時間がかかったりミスをしやすいという弱点があります。
そのため、この解法2が使える状況であれば今から紹介する方法で解くことをお勧めします。
(同じものを並べる順列の復習)
(復習問題1)1,1,1,2,2,3の6つの数字を並べる時、その場合の数は何通りあるか?
「円順列とじゅず順列の解説記事」の『同じものを並べる〜』に詳しい解説を載せているので、曖昧な人は確認しておいてください。
(解説):まず6つの数字を違うものとみなして、6!(通り)。
これを重複する数字(1が3つと2が2つ)分で割ることで、$$結果\frac{6!}{3! \times 2!}=60(通り)・・・答え$$
この方法を用います。つまり、
上へ行く"↑"と右へ行く"→"を並べる順列とみなして解く
方法をとります。まずは以下の図をご覧ください。
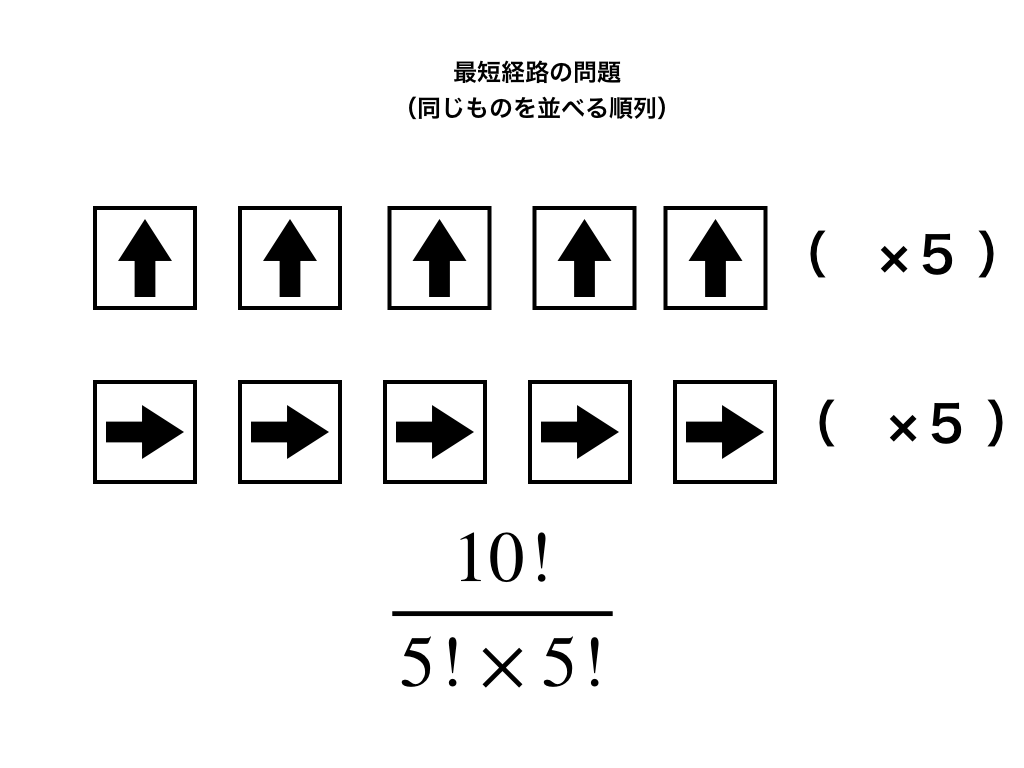
点A から下や左に戻らずに、5つ上かつ5つ右にある点Bに向かうので、1マス上へ上がることを”↑”、1マス右へ行くことを”→”とすると、↑は5つ,→も5つ選ぶことができます。
つまり、合わせて10個の矢印の並べ方を変えることによって道順が変化します。
(例:→、→、→、→、→、↑、↑、↑、↑、↑:という並べ方ならば、『5回連続右へ』進み、その後『5回連続上へ進んで』点Bに至る道順と対応します)
ただし、右矢印と上矢印は区別がつかないので、先ほど復習した同じものを並べる順列の解法を用いて、
$$\frac{10!}{5! \times 5!}=\frac{10\times 9\times 8\times 7\times 6}{5\times 4\times 3\times 2\times 1}$$
これを計算すると、252(通り)・・(答)
確かに、書き込み法の結果と同じ答えとなりました。
実践問題(余事象や書き込み法の応用)
ここでは、もう一歩踏み込んで『AからB』へ進む途中で、『指示された点を”必ず通る”場合の数』を求める問題や、反対に『ある点を”通らない”場合の数をもとめる問題』についての解き方を解説していきます。
ある点を必ず通る場合の数の問題
ではここまでで学習した知識を使いながら、実際の入試などで頻出のもう少し複雑な問題を解いていきましょう。
例題:次の図の点Aから点Bまでを最短で行く道順の場合の数を求めよ。ただし途中で必ず点Cを通るものとする。
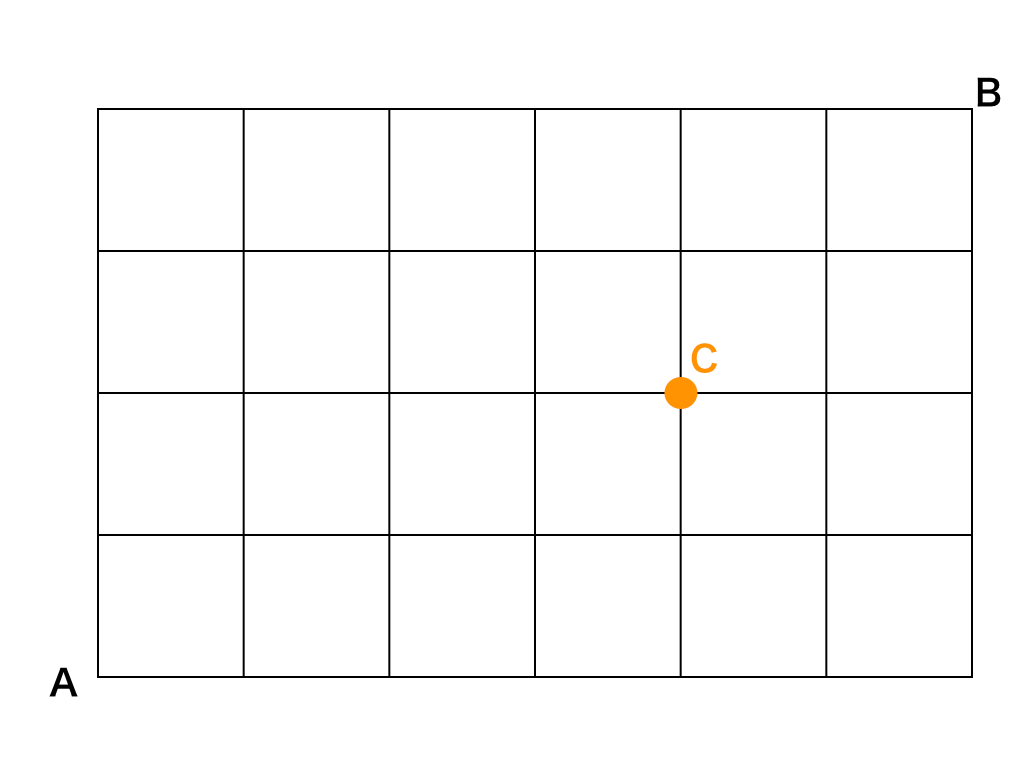
このような『必ず〜を通る』というパターンに対しては、次のように図を書き換えて問題を解いていきます。
解き方:図を書き換えて積の法則を使う
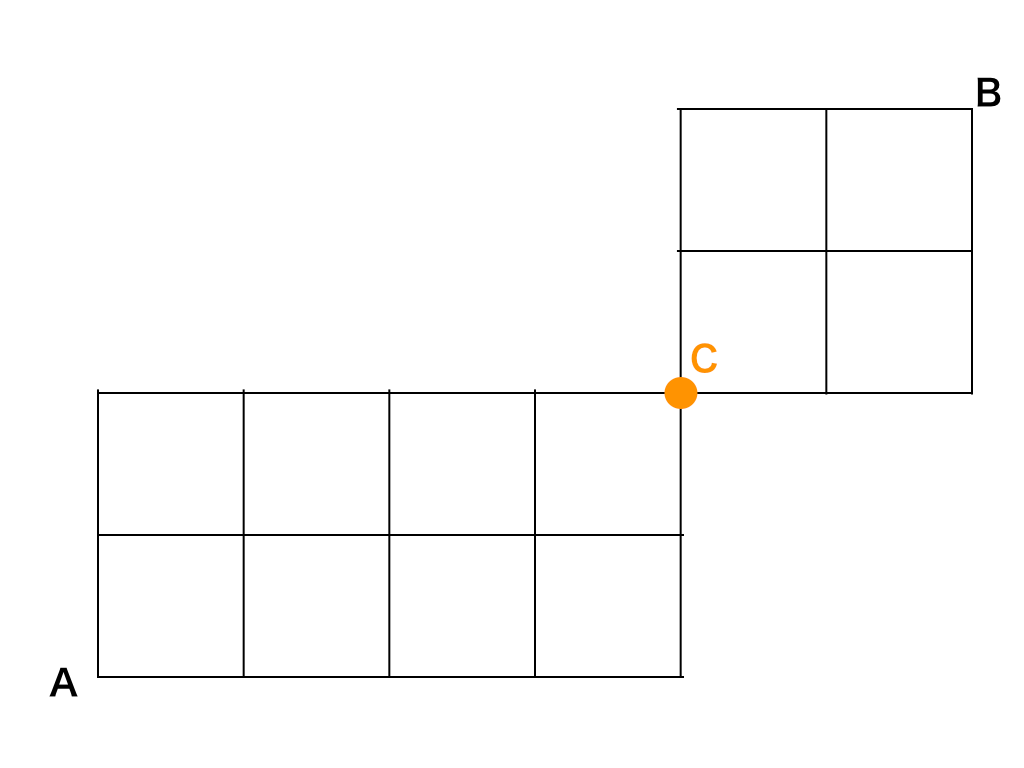
点Cを通る経路だけを取り出しました。ここで、(点A→点Cまでの経路の数)×(点C→点Bまでの経路の数)を計算する事で問題を解くことができます。
$$A→C:\frac{6!}{2!\cdot 4!}=15$$
かつ
$$C→B:\frac{4!}{2!\cdot 2!}=6$$
をそれぞれ求めて積を計算すると、
15×6=90(通り)・・・(答)
二点を必ず通る応用問題
上の『途中である1点を必ず通る』問題を『《ある2点》を必ず通る』に発展させた問題です。
解法は同じなので是非チャレンジしてみましょう。
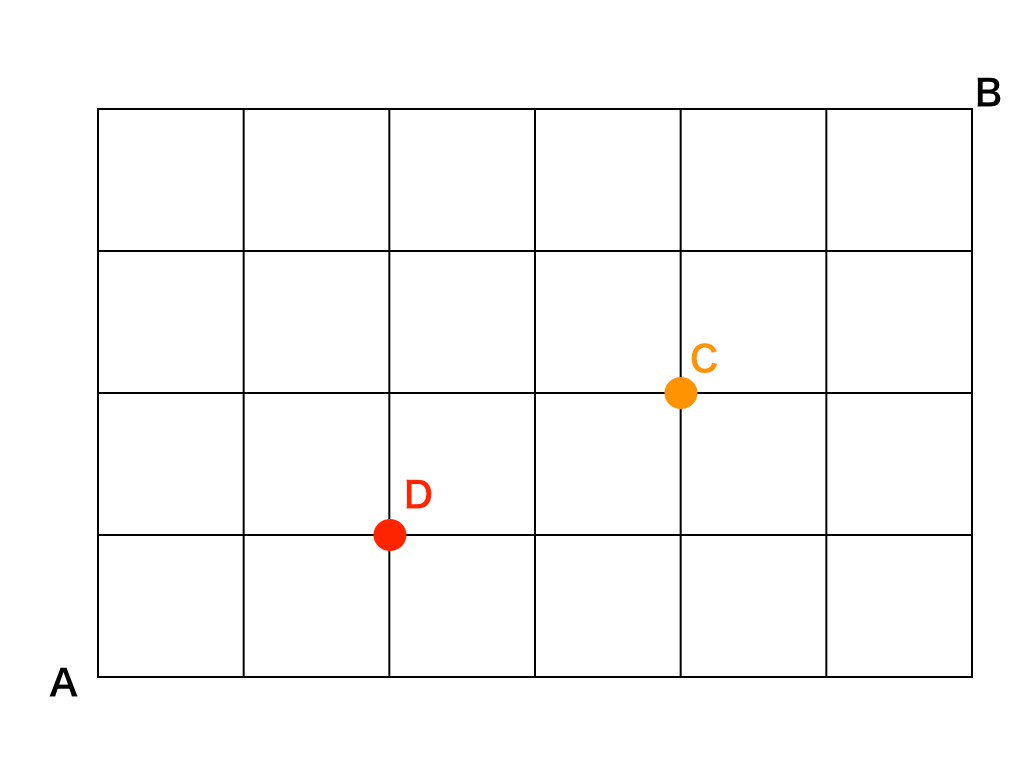
例題3:上のAからBまで向かう最短の経路のうち、途中で必ず点Cおよび点Dを通る場合の数は何通りあるか。
解説:途中2点を通る道順
この場合は、先ほどの図をさらに分けて3種類の場合の数を掛け合わせて答えを求めます。
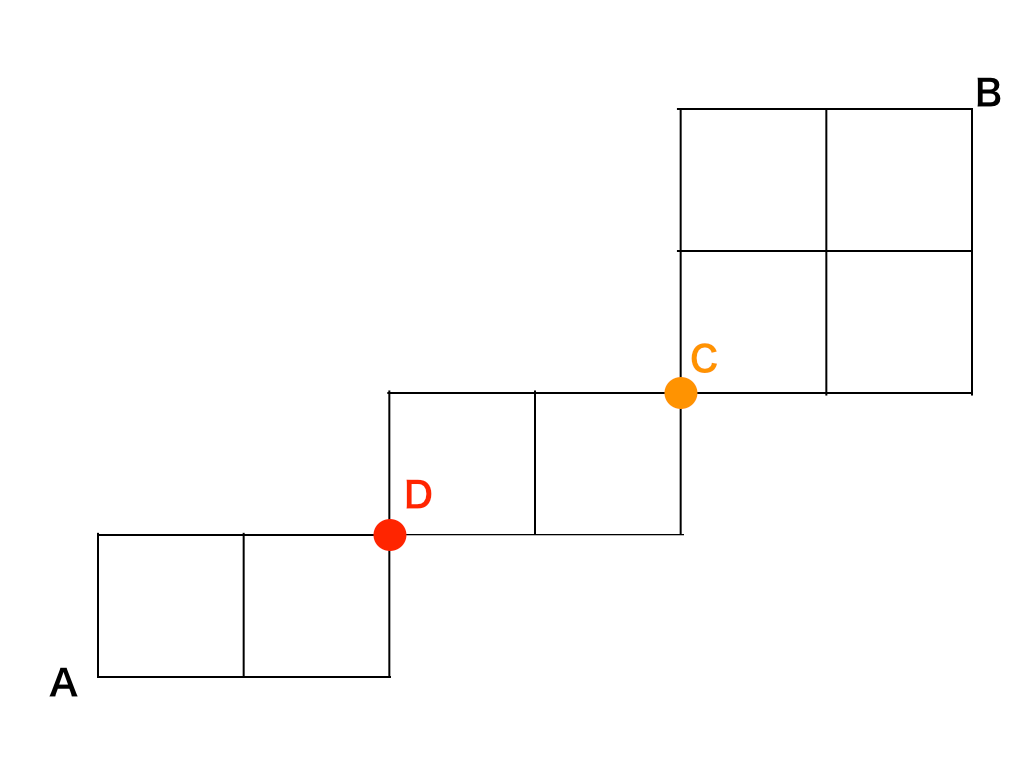
A→DとD→CとC→Bに分けるだけなので、$$\frac{3!}{2!}×\frac{3!}{2!}×\frac{4!}{2!\cdot 2!}=54(通り)$$
ある点を通らない最短経路の問題
この記事で紹介している”経路や道順関連”の問題で一番面倒なのが『ある点を通らない』という条件がある場合です。
この時にも2通りの解法があるのでそれぞれ紹介します。
例題4:次のような碁盤の目のような経路を、点Aから点Bまで後戻りすることなく進む。
この際に点Cを通ってはならないとするならば、その道順は全部で何通りあるか。
解法1で解く(ある点を消して書き込む)
まずは基本的な【書き込み法】を使って解いてみましょう。注意が必要なことは1方向しか進めないところ(点C周辺の場所)です。
具体的には20(通り)の場所から右へ1マス進んだところも20(通り)となり、点Cの右下の6(通り)から一つ上のマスに進む時も6(通り)となっています。
これは「6通りの場所から上へ1つ進む方法はただ一通りしかない」ので、そのまま数字を変えることなく書き込んでいます。(これは20通りの場所も同様です)
機械的に『書き込み法』を使っていると、このような少しひねった問題に対応できなくなります。
ただ足し算を繰り返して解いていくのではなく、”何をしているか”を理解しながら数字を書き込むようにしていきましょう。
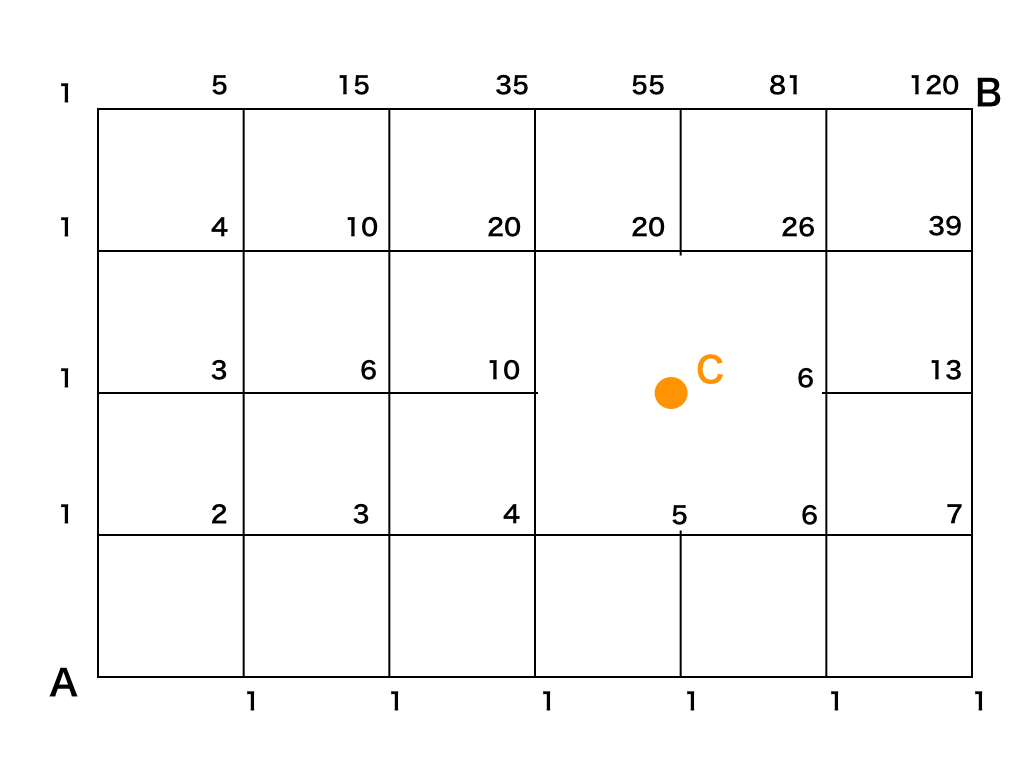
問題の図から点Cへ繋がる道を消した上で書き込んでいます。
以上より、Cを通らずAからBへ最短で進む方法は《120(通り)》であることがわかりました。
解法2で解く(余事象を利用する)
普通の最短経路の問題同様、この方法は少し面倒です。そこで【余事象】の考え方を使うとアッサリと答えを得られます。
(※余事象については、「余事象とは?使い方と意味を解説」を参考にしてください)
解法2:
余事象利用型の手順(1):点Cを通る場合も含めた全ての場合の数を求めます。
ここでは、上に↑×4、右に→×6なので
$$\frac{10!}{4!\times 6!}=\frac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}=210(通り)$$
手順2:先ほどの点Cを必ず通る(=余事象)場合の数を、積の法則を用いて求める。

$$\frac{6!}{4!2!}\times \frac{4!}{2!\cdot 2!}=90$$
手順3:全体ー(余事象)=求める場合の数より、
210ー90=120(通り)・・・(答)
こちらの方法でも120通りとなって2つの方法の答えが一致しました。
最短経路と場合の数まとめ
・「書き込み方」/「矢印を経路と対応させて、階乗を用いて解く方法」は両方とも重要なので『意味を理解した上で』使いこなせるようにしておきましょう。
・余事象/書き込み/積の法則/同じ矢印を並べる順列の求め方、のそれぞれをうまく組み合わせていくことでこの分野の問題はマスターできます。(問題集などで類題を探して解いてみてください!)
※:最短経路の応用として→「ランダムウォークと確率の問題」を作成しました。是非続けてご覧下さい。
場合の数と確率シリーズ一覧【SPI対策にも】
今回の内容を含め、【場合の数と確率】の分野では知っておかないといけない”解法や公式”がたくさん存在します。
そこで、「場合の数と確率の重要記事を総まとめ」←左の記事では、”PやCの公式の意味”といった入門レベルから、最難関大レベルの問題の解法まで、最小限の記憶で解くことができるノウハウをまとめています。
受験だけでなく、SPI非言語分野の対策にもご利用いただけます。
ぜひ続けてご覧ください!
今回も最後までご覧頂き、ありがとうございました。
当サイト「スマナビング!」では、読者の皆さんのご意見・ご感想の募集を、コメント欄にて行なっています。
お役に立ちましたら、 いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

