
コンデンサー回路の解法と電荷保存などの注意点
<今回の内容>:「電流と回路シリーズ」第4回として、コンデンサーが回路に入った問題の解き方を例題とともに紹介して行きます。
これまでの単純な抵抗と電池だけの回路とは異なり、コンデンサーには注意が必要な点がいくつかあるので(そして紛らわしい)、この記事でぜひコンデンサー回路の問題をマスターしましょう。
目次(タップした所へ飛びます)
コンデンサーと回路(復習/基礎)
実際に問題を解く前に、コンデンサーの知識の復習と、電気回路の問題に必須の知識を紹介していきます。
コンデンサーの仕組み/電気容量/用語の復習
コンデンサーは”電気を貯めておく装置”ということが出来、その仕組みは「コンデンサーの公式と仕組み(1)」で詳説しています。
このように説明すると、『電池』と『コンデンサー』の違いがわからなくなってしまう人がいます。
電池はあくまで”電位差を作り出すポンプ”のような役割をしているだけで『電池そのものが電気を蓄えているわけではない(一部の充電池などを除く)』ということを理解しておくことが大切です。
次に、コンデンサーが電気を貯めておくことができる理由は、2枚の金属板(極板)に電流を流し始めることで電池の+極と接続した方の極板に正電荷が、ー極と接続した方の極板に負電荷がたまります。
すると、極板はそれぞれ正と負の電気を帯び(磁石のN極とS極のように)クーロン力で引き合います。
これによって次第に電気(電荷)が動かなくなり、結果どんどんと電気がたまっていくのです。
コンデンサー関係の公式
$$極板の面積をS(m^{2}),極板間距離をd(m) $$
$$,真空の誘電率をε_{0}(\frac{F}{m}),$$
$$電気容量をC(F),電圧をV(V),電気量をQ(C)として、$$
$$Q(C)=C(F)V(V)$$
$$C(F)=ε_{0}(\frac{F}{m})\frac{S(m^{2})}{d(m)}$$
が言えます。電気容量については「コンデンサーの電気容量」を参照ください。
キルヒホッフの法則/オームの法則復習
ここでは、前回「キルヒホッフの第一/第二法則」とシリーズ第1回「I=envSとオームの法則」で扱った部分の簡単なおさらいをしておきます。
キルヒホッフの法則
第一法則:回路中のある点に流れ込んだ電流の総和と、その点から流れ出す電流の総和は等しい
第二法則:閉じた回路中での電圧上昇分の総和と電圧降下の総和は等しい
オームの法則
V(電圧)、I(電流)、R(抵抗)の間で、V=IRの関係が成り立つ
電荷保存則(孤立部分の電気量の和は常に等しい)の使い方のコツ【最重要】
コンデンサーの入った電気回路の問題を解くにあたって、最も大切な法則がこの『電荷(電気量)保存則』です。
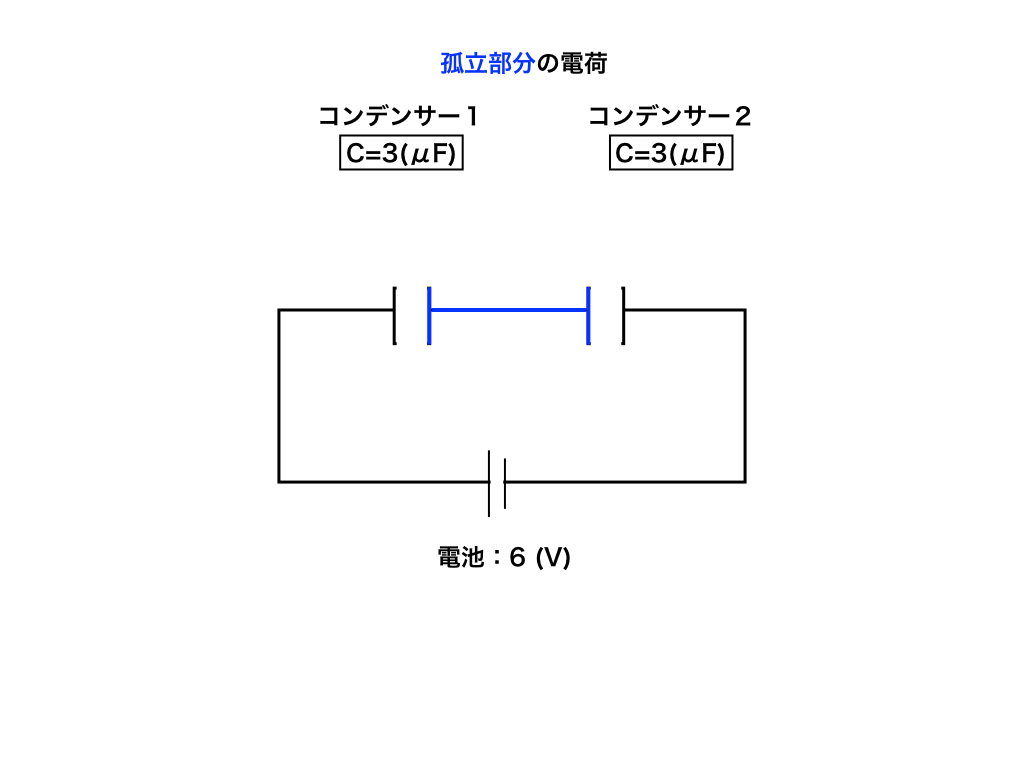
これは後の例題で扱う回路ですが、図中の青色で示した部分である『コンデンサー1の”電池の正極と直接繋がっていない方”の極板と、コンデンサー2の同じく”電池の負極とつながっていない方の極板”、そしてこの”2つの極板をつなぐ導線”』(回路中で島のように孤立しているので孤立部分と言ったりもします)の電気量は常に一定です。
すなわち、元々この青色の孤立部分に電気がたまっていなければ、電池と接続して充電されても次のように打ち消しあって0のままになります。
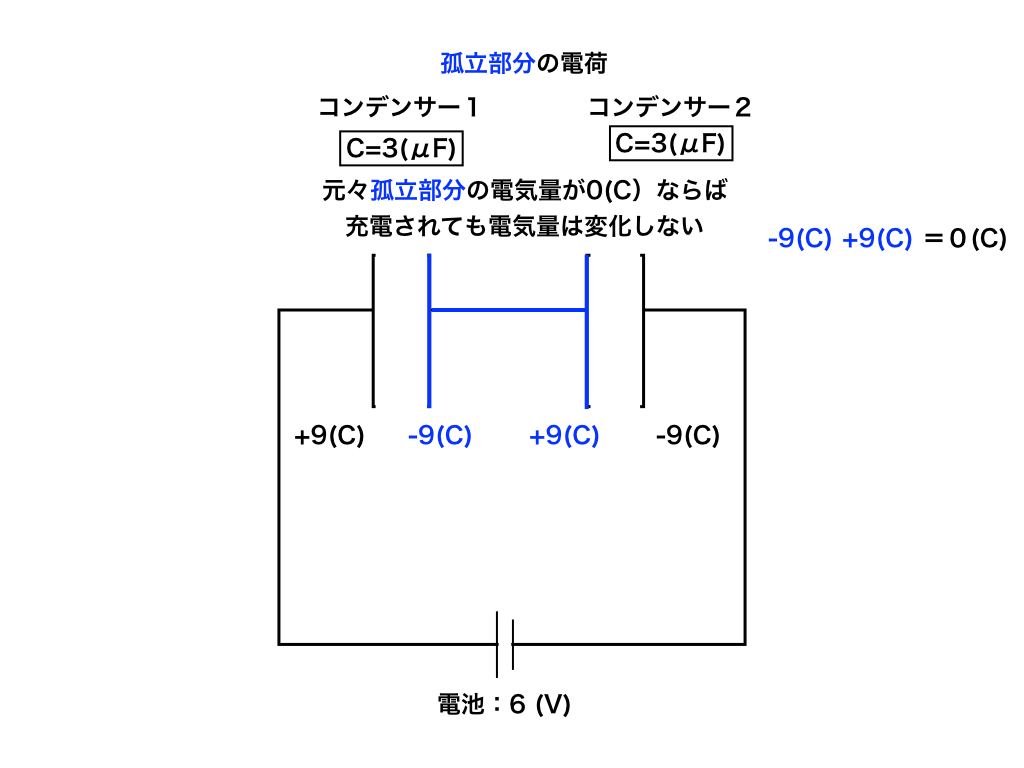
この考え方は、回路が複雑になっていくにつれてどんどん重要になるので是非頭に入れておきましょう。
コンデンサー入り回路の演習問題(実践編)
では、上で復習/習得した知識を使って、簡単な問題から解いて行きます。
電気容量と単位”μ”
なお、コンデンサーの電気容量の単位は上述したようにF(ファラド)でした。
が、現実にはこれほど大きな容量を持つコンデンサーは少なく、入試問題などでも”10のマイナス6乗”(100万分の1)を意味する『μ(マイクロ)』がついていることが多いです。
単位に注意しましょう
"十分時間が経過"と"接続(スイッチをon)にしてすぐ"がポイント
コンデンサーを含む回路の問題文では、『十分に時間が経過した時』や『スイッチを入れた時』といった言葉がよく出てきます。
詳しくは例題4のところで解説しますが、これらの言葉が登場したら
・『十分時間経過=コンデンサーの容量が満タンの状態=これ以上電流が流れない』
・『スイッチを入れた時=その瞬間にはコンデンサーには電気がたまっていない(注1)=コンデンサーを導線とみなす』
という発想にすぐ切り替える必要があります。
(注1):問題がさらに複雑になると、”元々コンデンサーに電気が蓄えられている”という場合があり、その時はべつに考えます。
実践問題
例題1;次の回路の図のように、電気容量が3μFのコンデンサーと起電力が6Vの電池を接続した。十分時間が経過した時、コンデンサーに蓄えられている電気量を求めよ。
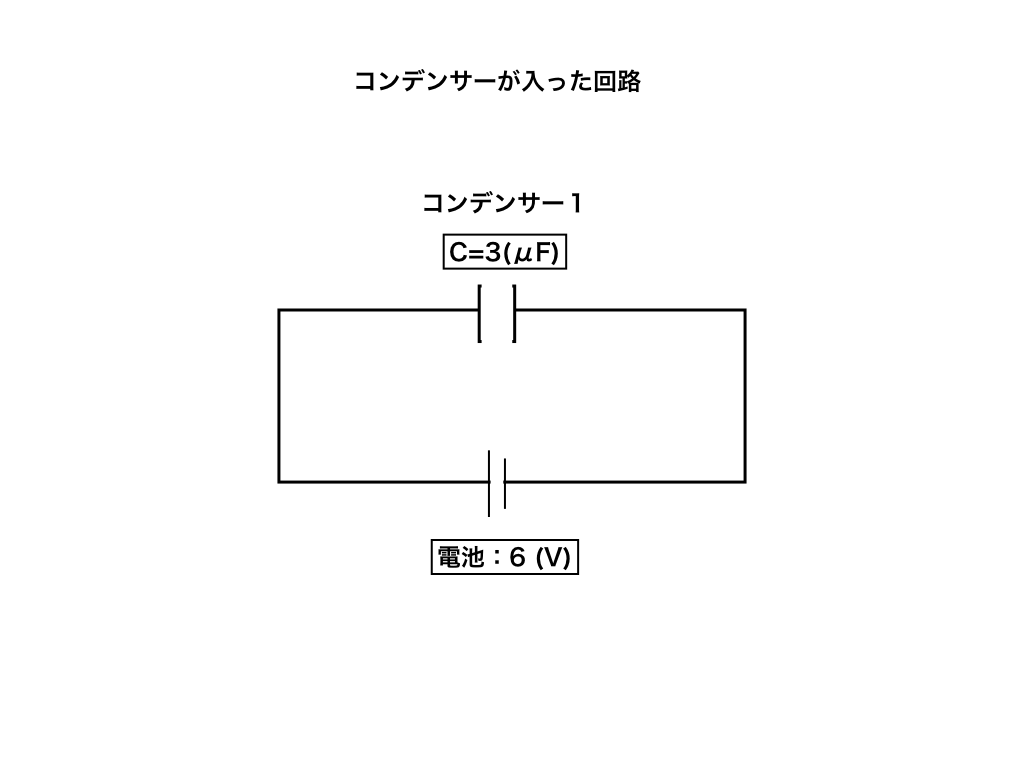
この問題は公式の確認用です。
例題2:直列接続
電気容量Cが3(μF)のコンデンサー2つを直列につなぎ、起電力が6(V)の電池と接続した。十分に時間が経過した時、それぞれのコンデンサーに蓄えられている電気量を求めよ。
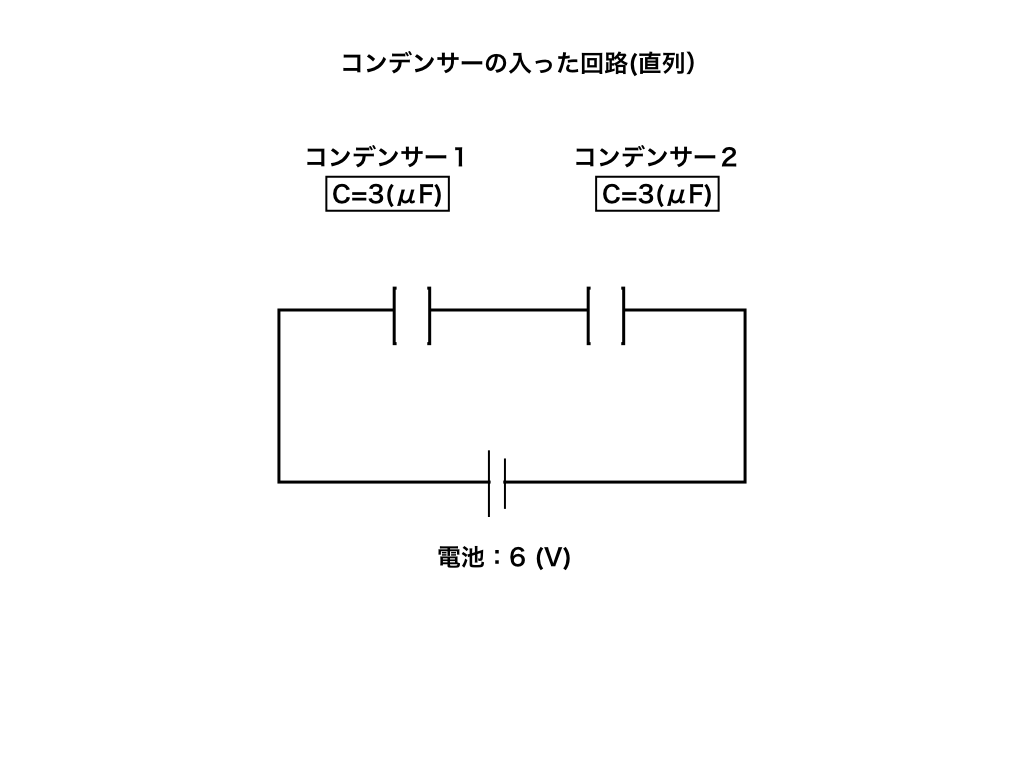
個数が増えて直列接続に変化しました。「コンデンサーの電気容量が変わるパターン」の記事を参考にして、解いてみてください。
例題3:並列接続
次のように電気容量が3(μF)のコンデンサー2つを並列にし、起電力E=6(V)の電池とつないだ。十分に時間が経過した時、それぞれのコンデンサー1・2に蓄えられている電気量(C)を求めよ。
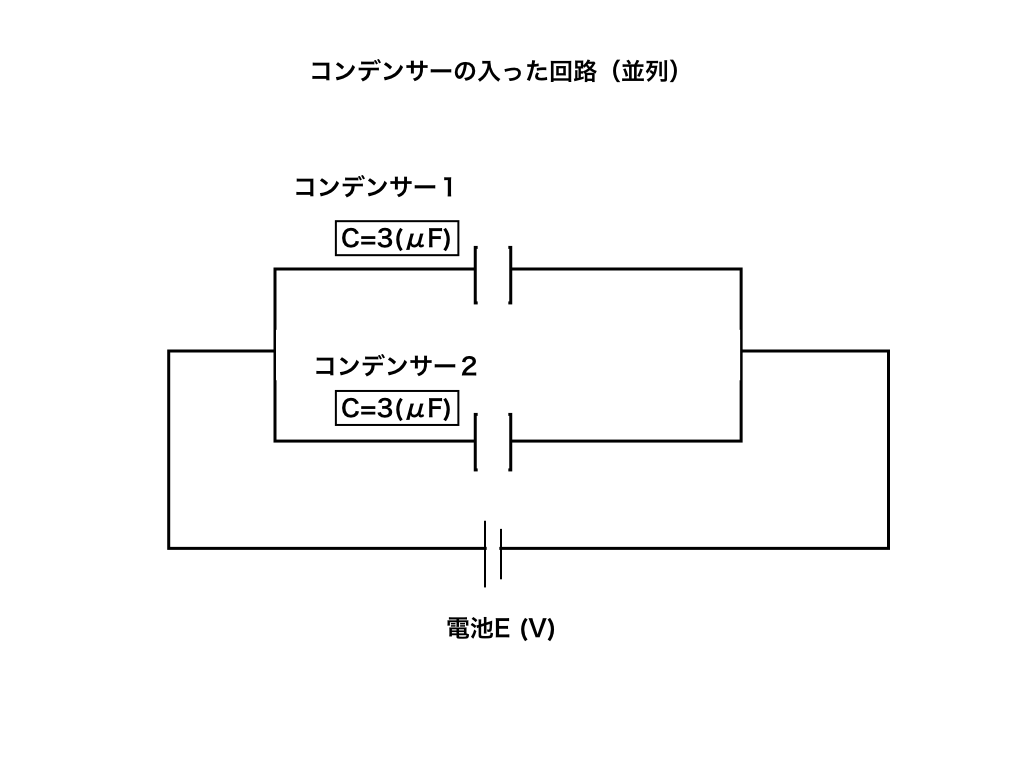
今度は並列接続です。例題2と同様に電気容量の合成やキルヒホッフの第二法則を参考にして解いていきましょう。
コンデンサ+抵抗+電池の回路の問題
例題4:次のように電気容量が3μFのコンデンサーと、抵抗値が2(Ω)の抵抗、さらに起電力が6(V)の電池を接続した。
回路をつないで(スイッチを入れて)すぐの時、抵抗R1に流れる電流と電圧、十分時間後にR1に流れる電流とコンデンサー1に溜まった電気量を求めよ。
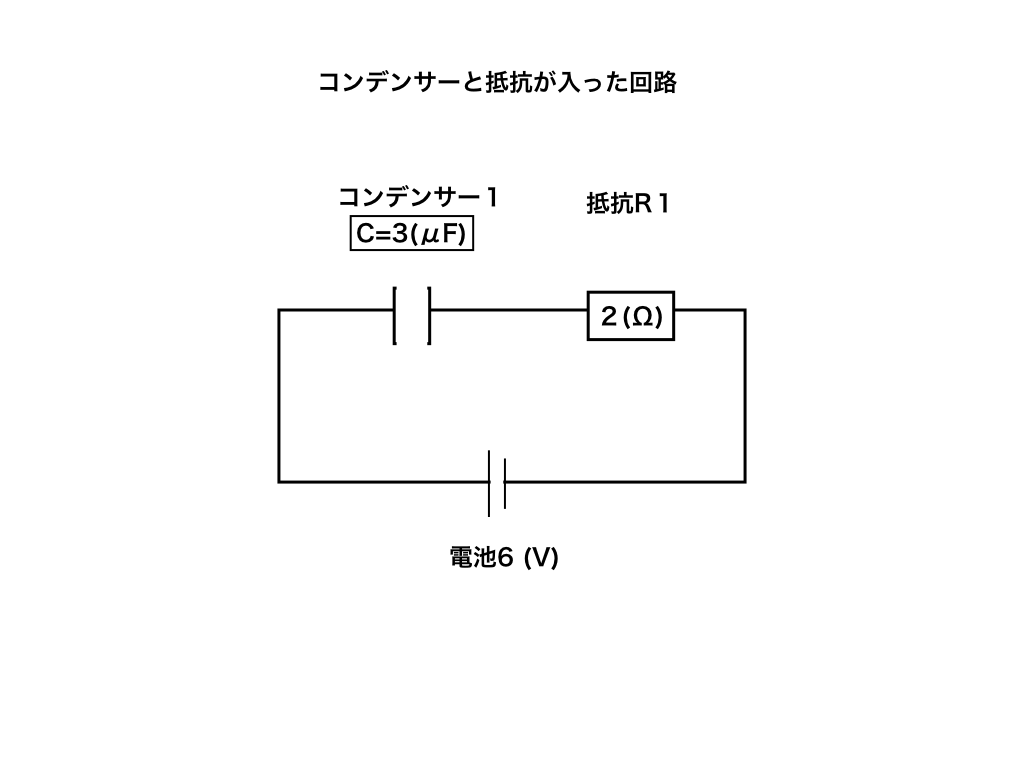
ここで解くコンデンサー+抵抗の問題は超頻出で、かつ回答の理由まで問われることが多い重要なものです。
回答解説
解答例題1:Q=CVの公式を用いて:Q=3(μF)×6(V)より、18μC(マイクロの単位に注意)
例題2:直列接続されているので、2つのコンデンサーを1つのコンデンサーと見做して計算すると、その電気容量は$$C_{1,2}=\frac{1}{C_{1}}+\frac{1}{C_{2}}$$
$$∴ C_{1,2}=\frac{3\dot 3}{3+3}=\frac{3}{2}$$
なので、$$Q_{1,2}=C_{1,2}\times 6(V) =9(μC)$$
極板のそれぞれに9(μC)がたまっている状態(先ほどの図を参照)なので、

コンデンサー1:9(μC)
コンデンサー2:9(μC)
例題3:今度は並列の場合なので、コンデンサー1、2両方に同じ電圧E=6(V)がかかります。
$$∴3\times 6=18(μC)$$
解答4:まず初めに、スイッチを入れた直後について考えます。
上述したようにこの時点ではコンデンサーに電荷は蓄えられておらず、『導線とみなす』ことが出来ます。
よって、6(V)の電圧は全て抵抗R1にかかります。ここでR1にかかる電圧と抵抗値がわかっているので、オームの法則より
$$6(V)=2(Ω)\times I(A) ∴I=3(A)$$
次に、『十分時間経過後』とあるので、コンデンサーは満タンの状態担っているはずです。よって、$$3(μF)\times 6(V)=18(μC)$$
さらに、コンデンサーはこれ以上電気を貯められない=電流を通さないため抵抗R1にも電流は流れません。
ゆえに、I=0(A)
直流回路(コンデンサー入り)まとめと続編
・今回はコンデンサーを含む回路の基礎を扱いました。次回はもう少し複雑な問題の解き方を紹介します
・いくつかの重要なキーワード『十分時間』や『スイッチを入れた時』などに注意して問題を解いていきましょう。
・「高校物理の電磁気分野総まとめ」にて、電磁気の解説記事をまとめています。是非続けてご覧ください!
「電流と電気回路」シリーズ一覧
電気分野のシリーズ一覧です。
第一回:「電流とは?I=envsの導出からオームの法則まで」
第二回:「非線形抵抗の問題と、特性曲線との交点が答えになるわけ」
第三回:「キルヒホッフの法則を徹底解説」
第四回:「今ココです」
第五回:「(作成中です)」
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集をコメント欄にて行なっています。 また、
いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

