消費電力Pと抵抗線(電気)による熱+(熱力学)
<この記事の内容>:電気分野の『抵抗』・『電力』などの基礎的な分野から、その応用問題、さらに『熱力学』の比熱などの知識を必要とする抵抗線による水槽の温度変化の問題まで分野を横断して解説していきます。
<関連記事>:「電磁気分野の解説記事〜総まとめ〜」
目次(タップした所へ飛びます)
消費電力の基本【単位に注意】
先ずは「消費電力」、「電力」、「仕事」と行ったそれぞれの意味と単位・公式を説明し、まとめていきます。
電力とは(基本公式や定義)
電力P:抵抗値がR(Ω)の抵抗にV(ボルト)、I(A)を流した時の「単位時間」あたりの仕事率。(ここがヤヤコシイと感じる人は、取り敢えず以下の式を頭に入れておきましょう)
P=VI(電力(W=J/s)は電圧(V)と電流(A)の積)
Q=Pt(電力(W)と時間(s)の積は発生する熱エネルギー(J)に等しい)
オームの法則との融合
V=IR(オームの法則)を”P=IV”に代入してできる”\(P=VI^{2}\)”や\(P=\Large{\frac{V^{2}}{R}}\)を使うこともしばしばあります。
(※:参考「オームの法則と電流の記事」にて、電流”I=envS”から、オームの法則の導出に至るまで解説しています。)
可変抵抗と消費電力Pの最大(応用)
応用問題一:いま、以下の<図一>のように可変抵抗Rxと抵抗Rが直列につながっている。
(1):可変抵抗Rxの値を変化させて、Rxの消費電力Pxが最大となるようにするには、Rxの抵抗値をいくらにすれば良いか。
(2):また、その時の消費電力の値も求めよ。
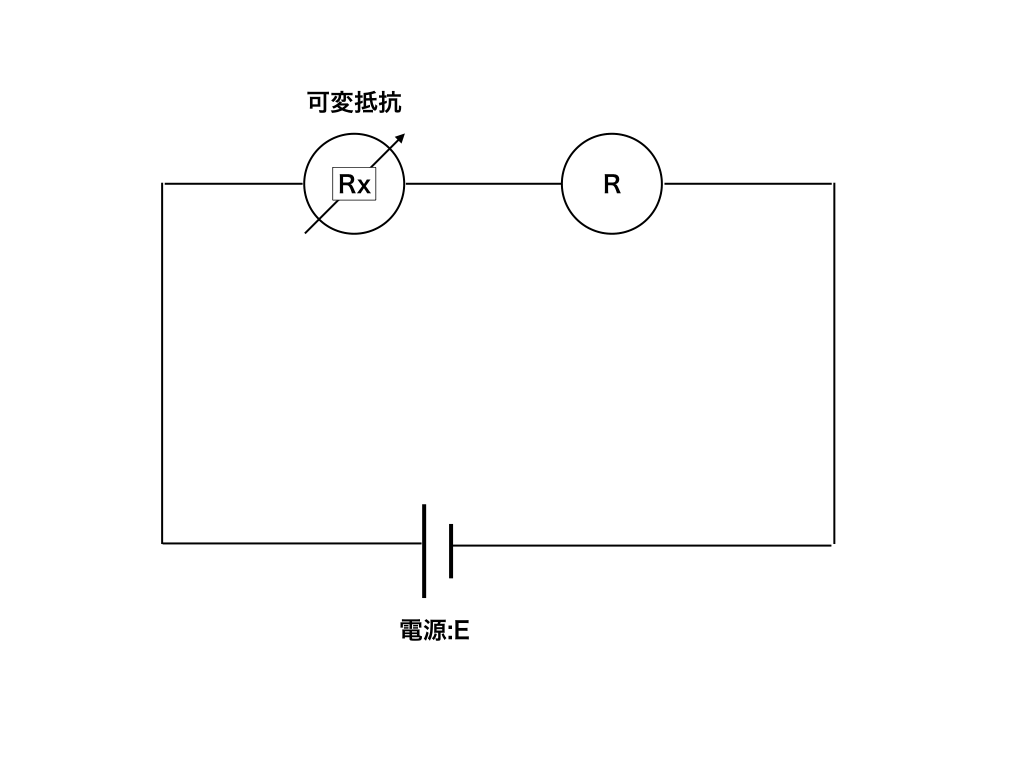
<図:Q一>
解説編(応用問題一)
(1):とりあえず、直列であるので電流は二つの抵抗どちらにも同じ値だけ流れます。
オームの法則より、
\(I=\Large{\frac{E}{R_{x}+R_{1}}}\)
\(P_{x}=R_{x}\cdot I^{2}\)
\(I^{2}\)に代入して、$$P_{x}=\frac{R_{x}\cdot E^{2}}{(R_{x}+R_{1})^{2}}$$
展開すると
\(P_{x}=\Large{\frac{R_{x}\cdot E^{2}}{R_{x}^{2}+2R_{x}R_{1}+ R_{1}^{2}}}\)
分子にある\(R_{x}\)を分母分子から\(R_{x}\)で割ることで消しておきます。
ここで、消費電力がMaxになるには式の分母が最小になればよい(極端な例で考えると、分母が0に近づくと無限大に発散します)が、実際には分母が取りうる最小値を数学の知識で求めます。
分母の最小→平方完成(この問題の最大のポイント)
$$P_{x}=\frac{E^{2}}{R_{x}+2R_{1}+\frac{R_{1}^{2}}{R_{x}}}$$
の分母を平方完成して最小値とその時の\(R_{x}\)を求めます。
\(P_{x}=\Large\frac{E^{2}}{(\sqrt{Rx}-\frac{R_{1}}{\sqrt{Rx}})^{2}+4R_{1}}\)
よって、\(\sqrt{R_{x}}=\frac{R_{1}}{\sqrt{Rx}}\)、つまり \(Rx=R_{1}\)の時、・・・(1)の答。
\(P_{x}=\Large{\frac{E^{2}}{4R_{1}}}\)で最大。・・・(2)の答。
相加・相乗平均を使った解法
上では平方完成を利用して計算しましたが、『最小値を求める→相加・相乗平均の利用』という考え方でも解くことができます。(※参考記事:「”指数・対数”不等式・方程式と『相加・相乗平均』の解説」)
分母に注目して、
\(\cdots (分母)=Rx+2R_{1}+\frac{R_{1}^{2}}{\sqrt{Rx}}\)
ここで、\(2R_{1}\)以外の2つに注目すると、掛けて一定である事から
$$Rx+\frac{R_{1}^{2}}{Rx}\geq 2\sqrt{Rx\times \frac{R_{1}^{2}}{Rx}}$$
ゆえに、\(Rx+\frac{R_{1}^{2}}{Rx}\geq 2R_{1}\)(等号成立条件はRx=R1のとき)・・・(1)
最小値が\(2R_{1}\)だから、\((分母)=2R_{1}+2R_{1}=4R_{1}\)
結果的に、平方完成で求めた\(P_{x}=\Large{\frac{E^{2}}{4R_{1}}}\)と同じとなります。・・・(2)
抵抗線による熱
上述しているように、この範囲は電磁気だけでなく、「熱力学」(や一部熱化学)の知識・公式・考え方を使います。
比熱・熱容量など熱力学の基礎
まず比熱ですが、ごく単純なもので『ある物質1(g)を1(K)上昇させる際に必要な(J)』をさします。
熱容量は、ある物体全体を1(K)上昇させるために必要なエネルギー(J)を意味します。「物質の3態と熱量(化学)の後半で解説」しているので、詳しくはそちらを参考にしてください。
抵抗による温度上昇(熱力学+電気融合問題)
融合問題二:以下の問題図のように、E(V)の電源に直列に接続した二つの抵抗\(R_{A}とR_{B}\)があり、抵抗値は同じであるとする。
この抵抗(電熱線)を2つの水槽A(水:100g),水槽B(水:質量不明)にそれぞれ入れて加熱する。
いま、水槽Aの温度上昇が水槽Bの温度上昇の”5倍”であった時、Bに入っている水の質量を求めよ。水の比熱をc(J/g・K)とする。
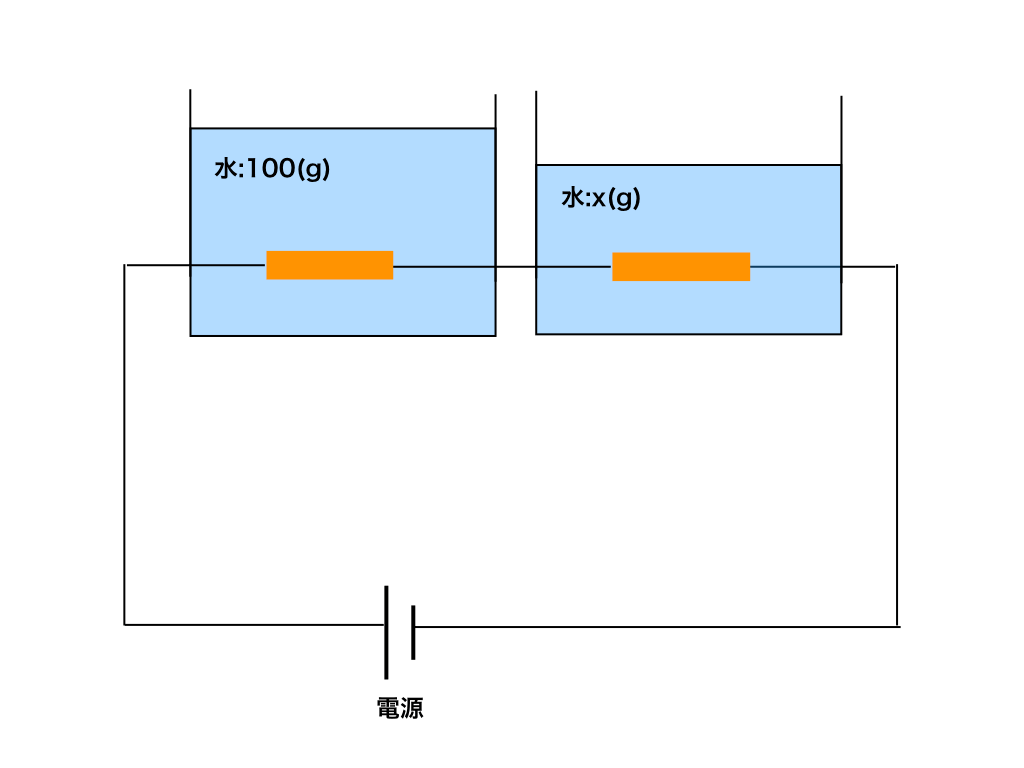
<Q二:図>
解答と解法の解説
まず指針を立てましょう。温度上昇の比(倍率)がわかっていて、どちらも同じ水(=つまり比熱が等しい)を温めています。その時間も同じです。
Aでの(J):\(Q_{A}=\Delta T_{A}\times c\times 100 \cdots (a)\)
Bでの(J):\(Q_{B}=\Delta T_{B}\times c\times x \cdots (b)\)
これで、A、Bでのジュール熱Qの式を立てることが出来たので、\(\Delta T_{A}=5\Delta T_{B}\)と\(Q_{A}=Q_{B}\)である事から、
\(\Delta T_{A}\times c\times 100=5\Delta T_{A}\times c\times x\)
故に、100=5x x=20(g)・・・(了)
この問題は、【抵抗値や溶液の種類】が同じだったので、この様に立式しなくても答えを予想できた人もいたかと思います。
実際の入試などでは、これらが違っていたり、《具体的な数値が与えられている》など上の解法を使わないと解くことが難しい問題が出されるので、ぜひ一連の流れを身に付けておいてください。
今回の《電気+熱力学》振り返りと続編へ
さて、熱力学との融合問題や、可変抵抗を含む回路の問題は少し工夫がいるので難しいと感じた人もいるかもしれません。
特にPの最大を求める問題は有名な問題なので、よく復習しておきましょう。
関連記事まとめ
今回も最後までご覧頂き、有難うございました。
【受験/学習メディア】:《スマホで学ぶサイト、スマナビング!》では,読者の皆さんのご意見・ご感想を募集しています。
コメント欄までぜひお寄せください。
(※・現在、”個別の問題や証明”などの質問には対応出来ない場合があります。)
・その他のお問い合わせ/ご依頼/タイアップなどに付きましては、引き続きお待ちしております。
本ページ上部の【運営元ページ】より直接ご連絡下さい。

