
電位と電場を「イメージ」する
今回は高校物理ー電磁気の入り口として、
点電荷が作る電位と電場について解説していきたいと思います。先にこの記事の結論を書いておきます。
「電位は高さ、電場は傾き:力学と対応して考えるとスッキリ理解できます。」
詳しい解説は以下よりご覧下さい!
高校範囲の電磁気に関する記事をまとめました。「電磁気の解説記事総まとめページ」よりご覧ください!
なお記事の中には少し複雑な部分があるので、完全に理解出来なくてもいい位の気持ちで読んでもらえればと思います。(*注1)
※2019/09/21:最新版に更新
目次(タップした所へ飛びます)
点電荷が作る電位と電場
まず初めは『点電荷』とは何か?など用語や公式の確認から見ていきます。
点電荷と試験電荷
点電荷とは、簡単に言えば正や負の電気を帯びた素粒子(物質を構成する最小単位)の事です。
高校生は非常に小さい、正か負かの電気を帯びたものと考えてもらって構いません。
試験電荷とは、 +1(C)の電気量を持った点電荷の事です。
クーロンの法則とファラデーの「電場」
クーロン力(静電気力)とは電荷と電荷の間に働く力です。違う種類の電荷同士は引き合い(引力)、同じ種類の電荷同士は反発(斥力)します。
これは磁石(のN極とS極)と同じなのでスムーズに理解出来ると思います。
そしてそのクーロン力の大きさをF(N)として、kを比例定数、r(m)を電荷間の距離、
q1、q2(C)をそれぞれの電気量と置いて公式にしたものが「クーロンの法則」です。
$$F=\frac {k| q_{1}| |q_{2}| }{r^{2}}$$
クーロン力の求め方にはもう一つ方法があり、それは「電場」という概念を用います。
場とは何か
「場」というものはこれから頻繁に出てきます。有名なものは「重力場」、「電場」、「磁場」・・・
一体「場」とは何なのでしょうか?おおまかなイメージとしては、何らかの物質に力を与える「空間」と言えそうです。
例えば、我々は重力場の中で生活しています。消しゴムを持ち上げて手を離すと消しゴムは落下していきます。
なぜ落下するか?「重力」によって消しゴムに下向きに力が加えられる「重力場」に居るからです。
(実際は、地球と消しゴムの万有引力によるものですが、地球と消しゴム間に働く万有引力はほぼ重力に近似できます)
では「電場」とは何なのか?
先の例を引くと、電荷にクーロン力を与える「空間」といえます。
電場はE(N/C)で表し、向きを持っています。したがってベクトル量となります。
ここで、もう一つのクーロン力の公式を紹介しましょう。
F(N)=Eq (qは電荷で単位は(C))
つまり”重力”場で、F=mgであった様にここでは”質量m”と”電荷q”が対応し、また、重力加速度”g”と”電場E”が対応していると考えられます。
点電荷の作る電場E
いま電気量+Q(C)の点電荷を固定します。そして、そこから距離”r(m)”離れた位置に電荷”+q1(C)”を置くとどうなるでしょうか?
どちらも正の電荷なので、斥力が働きq1電荷は離れて行きます。
クーロンの法則に代入すると、$$F=k\cdot \frac{Q\cdot q_{1}}{r^{2}}$$のクーロン力がq1電荷にかかる様です。
もう一つ、クーロン力を求める公式がありました。F=Eq です。
どちらも同じ力を受けるはずなので、Fは共通、よって、二つの公式を等式で結んで見ましょう。
E・q1=k・Q・q1/r2 と表せます。ここで、q1を消すと、$$E=k\cdot \frac{Q}{r^{2}}$$ という式が出てきます。これこそが、点電荷が作り出す電場の値なのです。
電位Vと電場Eのイメージ
先ほどと同じ様に、電荷+Q(C)と、電荷-Q(C)を<図2>の様に固定しておいておくことにします。
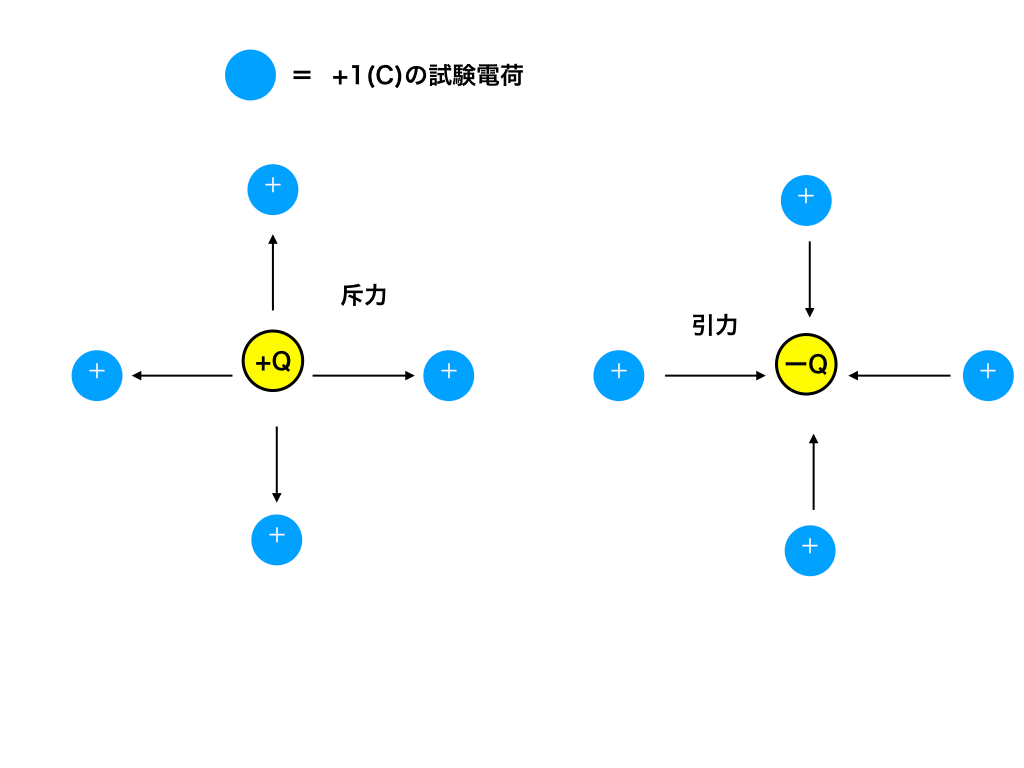
<図2:試験電荷が受ける斥力と引力>
この二つの電荷の周りに+1(C)の試験電荷をたくさんおいて見ましょう、
すると、斥力が働き+Q(C)の周りの試験電荷は斥力により四方八方へ離れて行きます。
また、 -Q(C)の周りの試験電荷は引力によって近づいて行きます。
これは+Qの電荷を山の頂点と見て、 -Qの電荷を谷の底の様に考えることが出来ないでしょうか?
<図3>を見て下さい。上の文をイメージ図にして見ました。
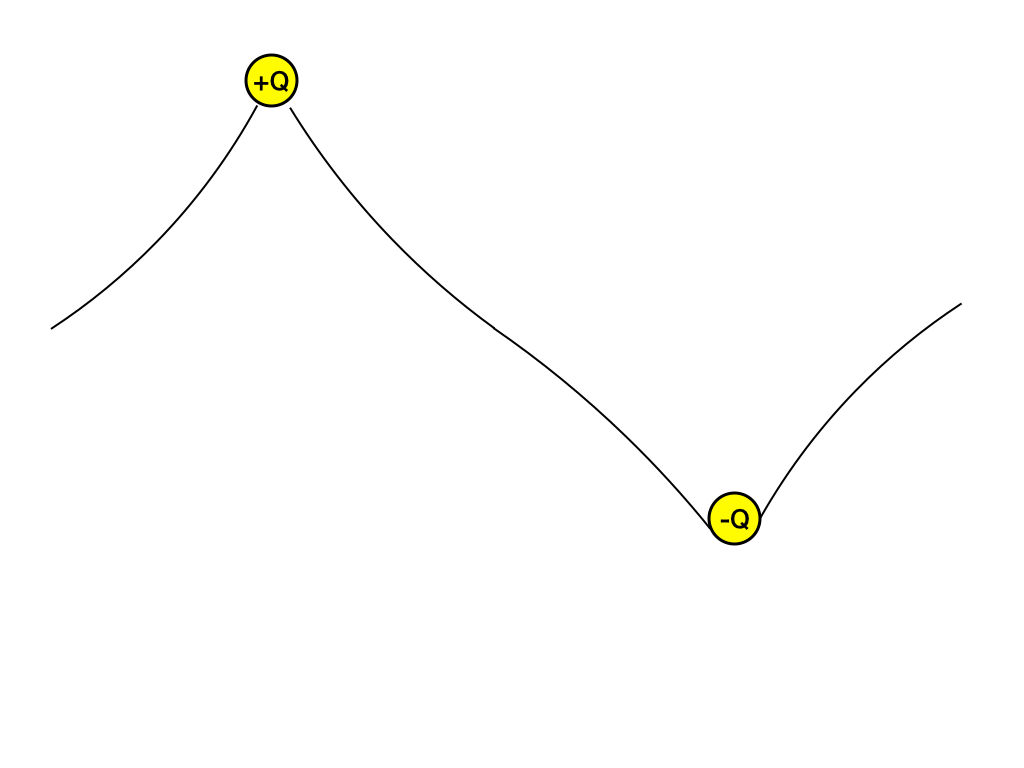
<図3:点電荷と高さ・傾きのイメージ>
この様に、点電荷の周りの様子を高低で見ておくと見通しがよくなります。
電位Vとは何か
電位の定義は、「クーロン力Fに逆らって、+1(C)の試験電荷を無限遠から任意の点A(r)まで動かした時に電荷が得るエネルギー」と言えます。
??な人も多いと思いますが、<図4>をみてください。
<図3>での山の部分だけを取り出して、無限に遠い所(無限遠)から正の試験電荷をE(図中で右向き)に逆らってrの位置まで<図4>の様に動かした仕事の事です。
もっと簡単に言えば、力学であった位置エネルギーの「位置」、つまり“高さ”に相当するのが電位Vです。
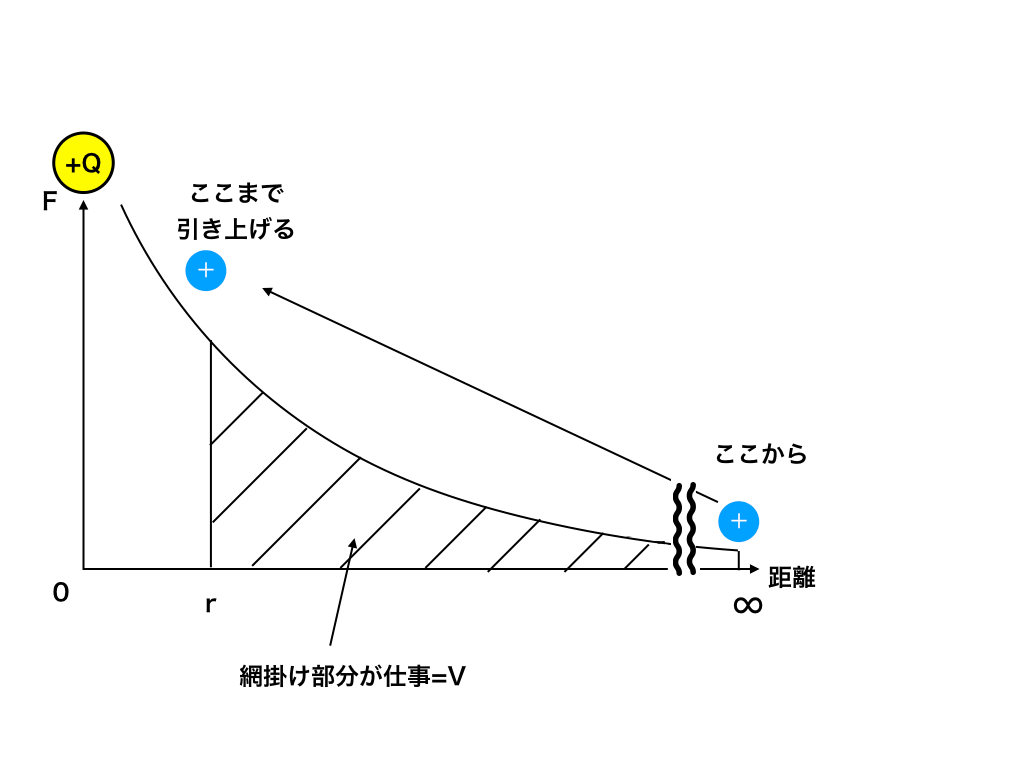
<図4:F-xグラフ>
電位の式の導出準備
では、実際に電位の公式を導出して見ましょう。普通、仕事=力×距離でした。
しかしクーロン力の場合には、山を登るに連れてどんどん必要な力が大きくなります。
(クーロン力が大きくなる)そのため<図4>である様に、一定の力×距離と簡単に計算できません。
そこで、積分が必要になります。
また、どこから点A(r)まで引き上げるかの基準点を決めないといけないですが、電場Eの影響を受けないところ(E=0)のところがベストです。
しかしどこまで離れても電場は弱くなっては行くものの0にはなりません。
そこで無限遠を基準にすると、E=k・Q/r2 のrに∞を代入すればE=0となってくれるので、基準点を∞とします。
電位Vの導出
次の様に$$V_{x}=-\int ^{r}_{\infty }Edx$$を計算すると、$$V=\frac {kQ}{r}$$と計算できます。この式が電位の公式です。以下に詳しく書いていきます。
Fに逆らって無限遠の基準点からrまで試験電荷を動かすので、負の符号が付いた、ーFをr(∞)からrまで距離で積分したものがVになります。
更に、クーロン力F=qE(N)で、電位の定義よりq=+1(C)から、F=Eとなるので、
結局電位は、上の定義のーFをーEに置き換えて積分したものと同じになります。
<参考>:「万有引力の位置エネルギーを導く」←の記事で、万有引力による位置エネルギーを導出しています。
興味があれば、この記事と対応させて読んでみてください!
(この辺りはかなりヤヤコシイので、難しいと思ったら流し読みしてもらって構いません)
$$V_{x}=-\int ^{r}_{\infty }Edx$$
$$=\int ^{\infty }_{r}k\frac {Q}{x^{2}}dx=[ -k\frac {Q}{x}] ^{\infty }_{r}$$
$$=-\frac {kQ}{\infty }-( -\frac {kQ}{r}) $$
$$V=\frac {kQ}{r}$$
結論:EとVの関係性
Vは電気的な「高さ」と言えました。ではEは?
Eを積分してVが出る様に、Vを微分するとEが求められます。(一度やって見て下さい。ただしEはベクトル量なので、符号に注意!)
では再び力学的に考えると、高さを微分すると、「傾き」になります。
したがってVは電気的な高さ、Eは傾きと考える事が出来ます。
以上、入門電磁気学でした。お疲れ様でした。
#2018/05/27加筆更新
#2018/08/29更新
!2018/09/23加筆更新!
電位・電場のまとめと関連記事
今回の内容を更に掘り下げて、【座標上の2つの点電荷が作る電場と電位・点電荷の力学との融合問題】を扱った記事を作成しました。
「点電荷」についてマスターしたい人は>>「複数の点電荷による電位・電場と点電荷の運動」をご覧ください。
現在この記事をもとにした電気力線とgaussの法則の記事を製作中です。2018/05/28公開予定。
→「電気力線とガウスの法則」作成しました。
電磁気分野のまとめ記事へ
<電磁気分野は「電気・磁気分野の解説記事まとめ」の記事を使って予習・復習しましょう!>
今回も最後までご覧いただき有難うございました。
感想や記事リクエスト、誤植等がありましたらコメント欄、もしくはお問い合わせページまでお願いいたします。
また、お役に立ちましたら、はてブ!、やいいね、Twitter等でシェアして頂けると嬉しいです!よろしくお願いします。
(*注1)この記事はあくまで高校範囲、かつ初学者向けに作成した物なので、大学以降の電磁気学よりも厳密さに欠ける部分も有りますがご了承下さい。

