オームの法則(2):抵抗率と非線形抵抗を詳しく!
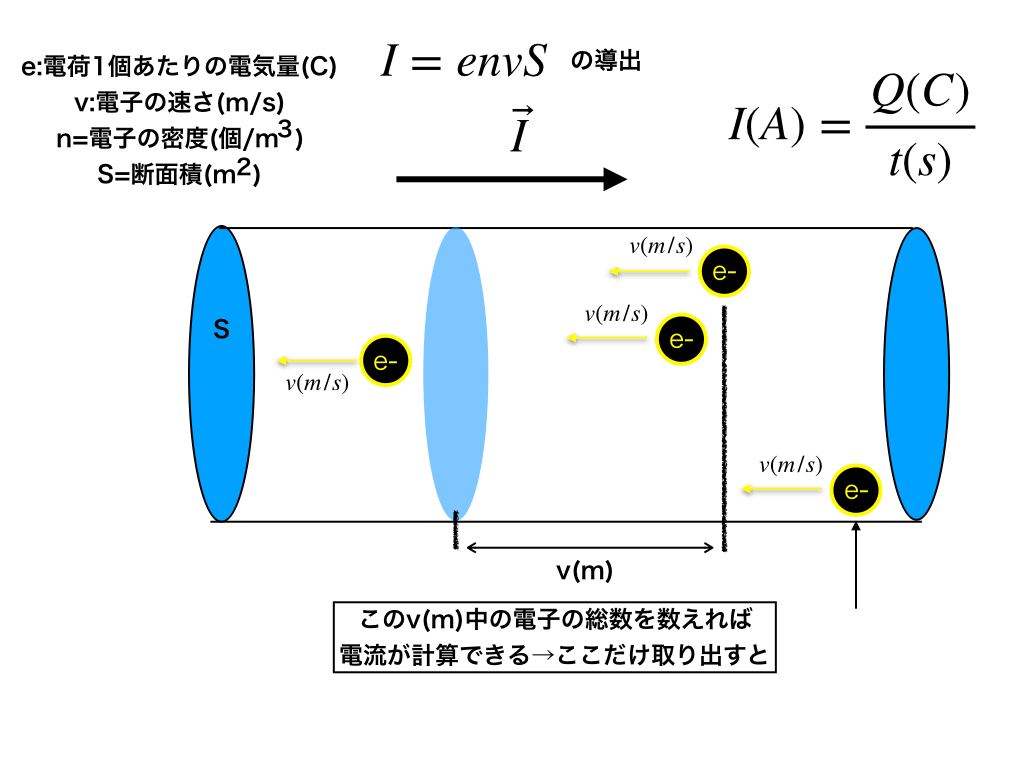
<この記事の内容>:「電流の式I=envsの導出とオームの法則(1)」に引き続き、
・今回は抵抗値R (Ω)の抵抗率ρが変化する理由や、温度との関係を解説し
・後半ではそれに伴ってオームの法則が成り立たない『非線形(オーム)抵抗』の問題の解き方を解説していきます。
<これまでの復習は「高校物理:電磁気の解法解説記事まとめ」をご利用ください>
(※)2019/10/02、式の一部を修正し更新しました。
目次(タップした所へ飛びます)
抵抗値Rと抵抗率ρの変化
ここまでは、『理想的な』状態でのオームの法則を見てきました。$$R=\rho\frac{l}{S}$$で、$$オームの法則:I=\frac{V}{R}$$
<図1>
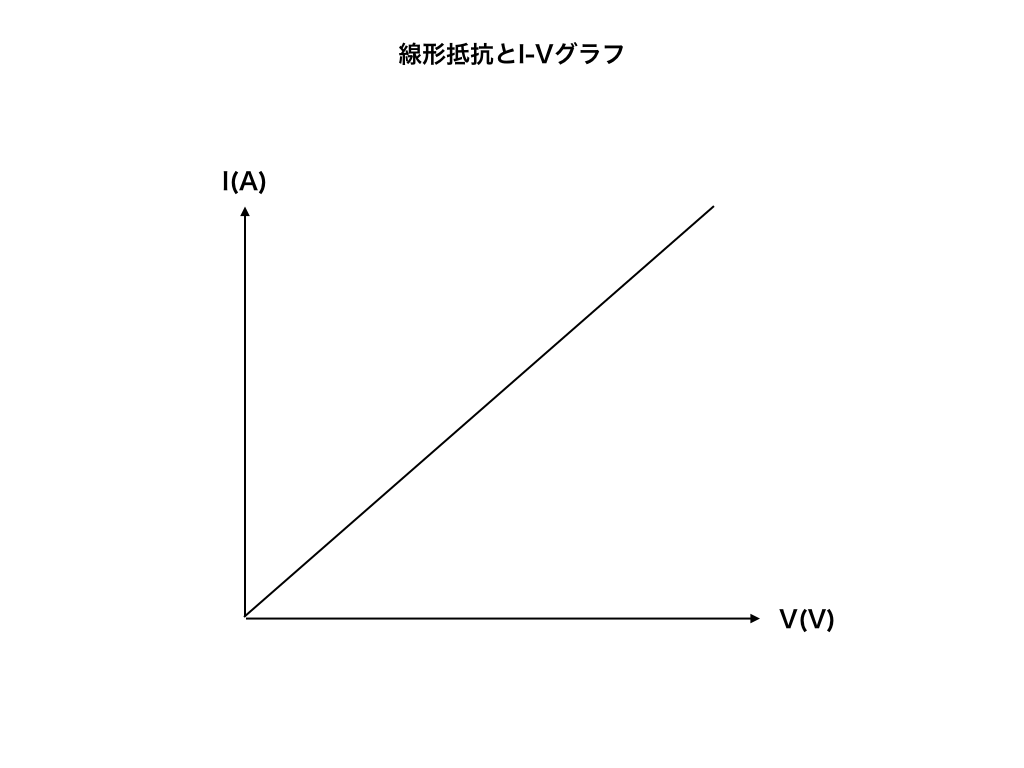
<オームの法則が成り立つ抵抗での電流ー電圧グラフ>
抵抗中の電子は真っ直ぐに進まない!
以下の<図2>のように、現実には電子が通る抵抗中に陽イオンがたくさん含まれています。
従って、<図1>のような真っ直ぐに電子が進むことができず、イオンとぶつかりながらジグザグに進んでいくことになります。
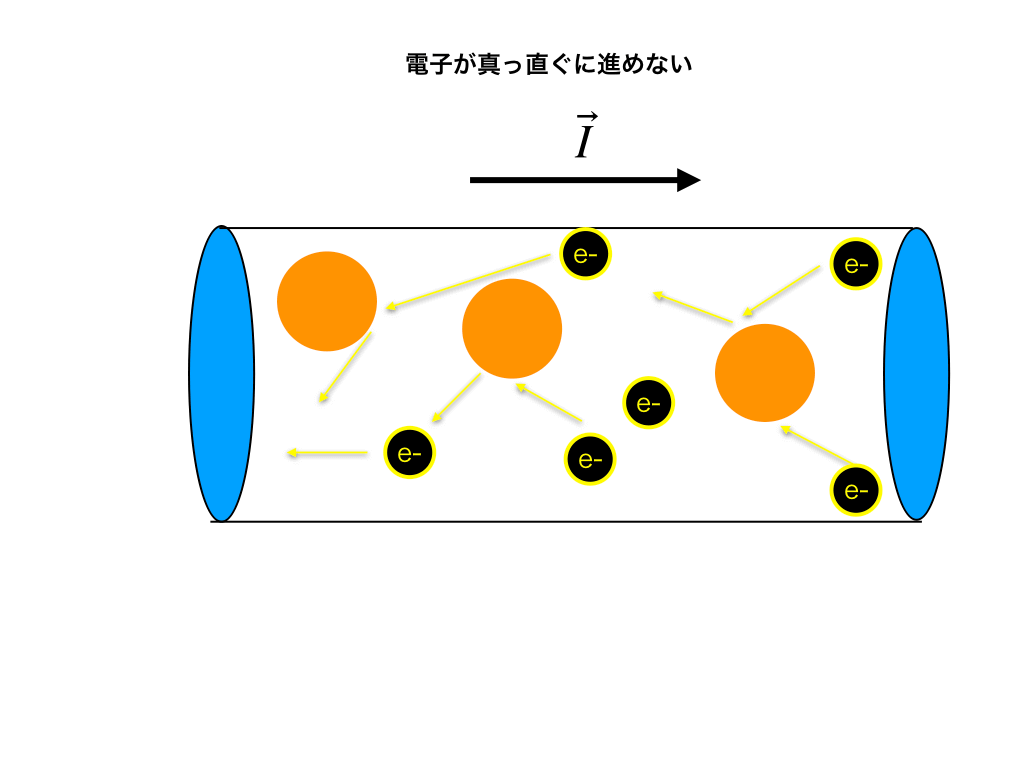
<図2>
さらに、抵抗の温度が上がるとともに陽イオンの運動(熱運動)が激しくなるので、より電子は真っ直ぐ進みにくくなり、抵抗値が大きくなります。
そのため、次の項で紹介する様な(温度ー抵抗値)の関係式が与えられた問題を解く事があります。
抵抗値Rと温度変化の関係式
まず抵抗率ρが上述した理由で次の式の様に変化します。
$$\rho=\rho_{0}(1+\alpha t)$$
$$ここで、抵抗値の式は:R=\rho \frac{l}{S}なので$$
$$R=R_{0}(1+αt) と書くことも出来ます。$$
(ρ0は0℃での抵抗率の値,αはその抵抗を構成する物質固有の値、tは温度です)
非線形(オーム)抵抗の問題の解き方
上記のような理由で、ρ、そしてRが変化するために、簡単にオームの法則を使って電流や電位差を求めることができない問題がよく出題されます。
そこで、この様な【I-V図でのRが非線形(以下の図の様に比例ではない)の場合】の問題を、《理想的な線形抵抗の場合と比べて》解説していきます。
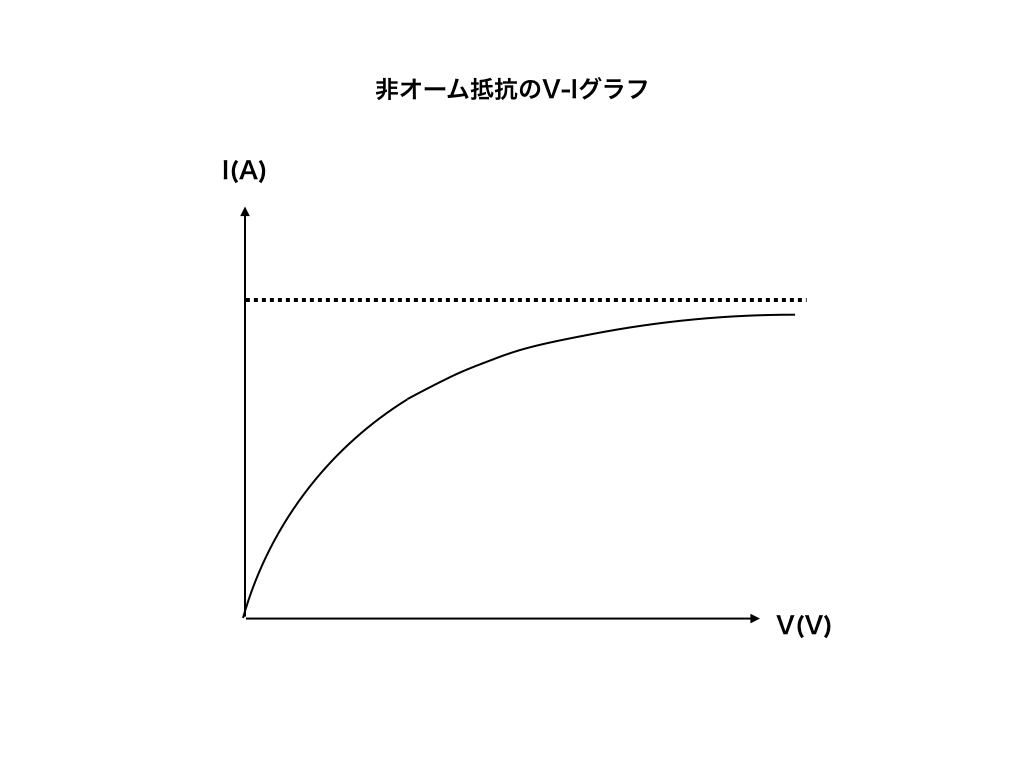
<非線形抵抗の電流ー電圧のグラフ>
線形抵抗の問題
線形抵抗の基本的な問題は次のようなものです。
電圧V(V)の電池と抵抗値R(Ω)の抵抗をつなげた回路がある。この時抵抗を流れる電流は何アンペアか。
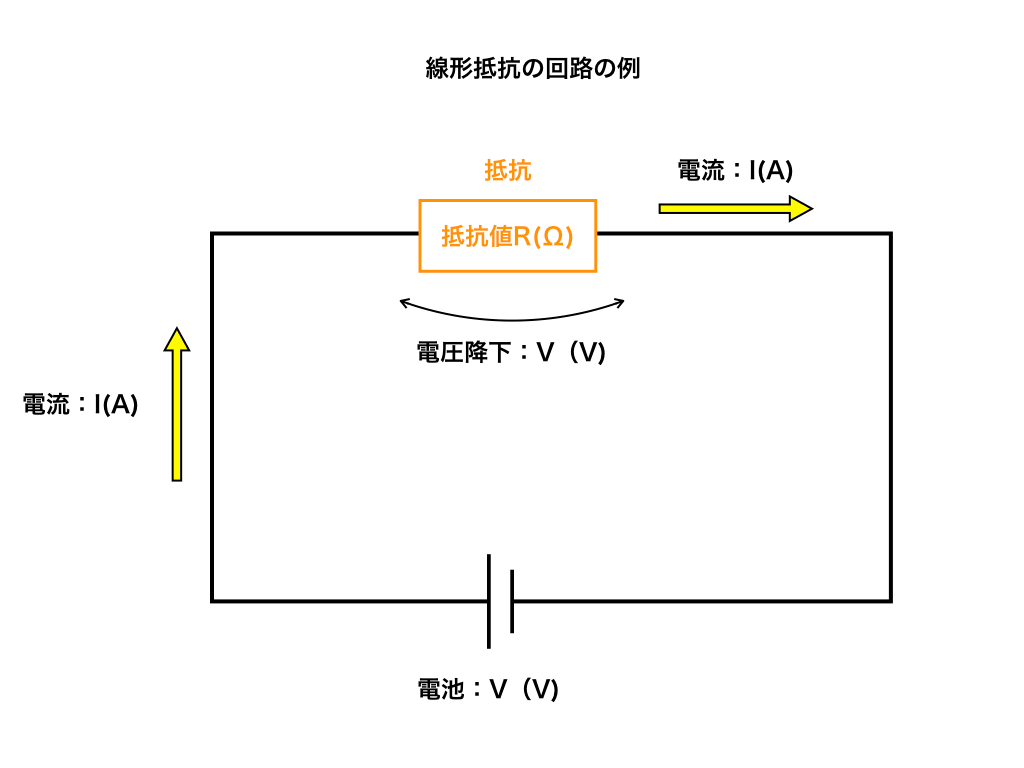
<問題1の回路図>
この様な問題は、単純にオームの法則を使う事で解が求まります。
抵抗にかかる電圧はV(V)で、抵抗値R、そしてオームの法則より$$I(A)=\frac{V}{R}$$
非線形(オーム)抵抗の問題
次に、非オーム抵抗の問題として代表的な、『電球を回路に入れた場合』を見てみましょう。
電圧E(V)の電池と抵抗値R(Ω)の抵抗、そして以下のグラフの様に非線形な抵抗値を持つ電球をつなげた回路がある。
このとき、電球を流れる電流と電圧をもとめよ。(グラフはイメージで、実際には目盛りがついたグラフが与えられます。)
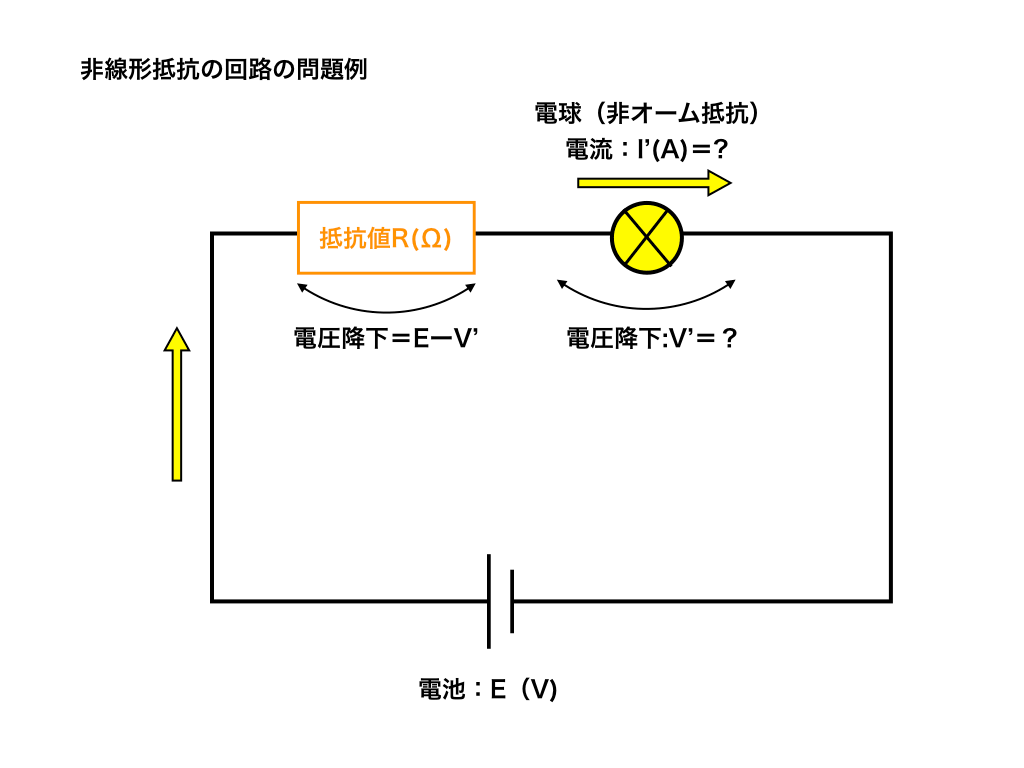
<問題2の回路図>
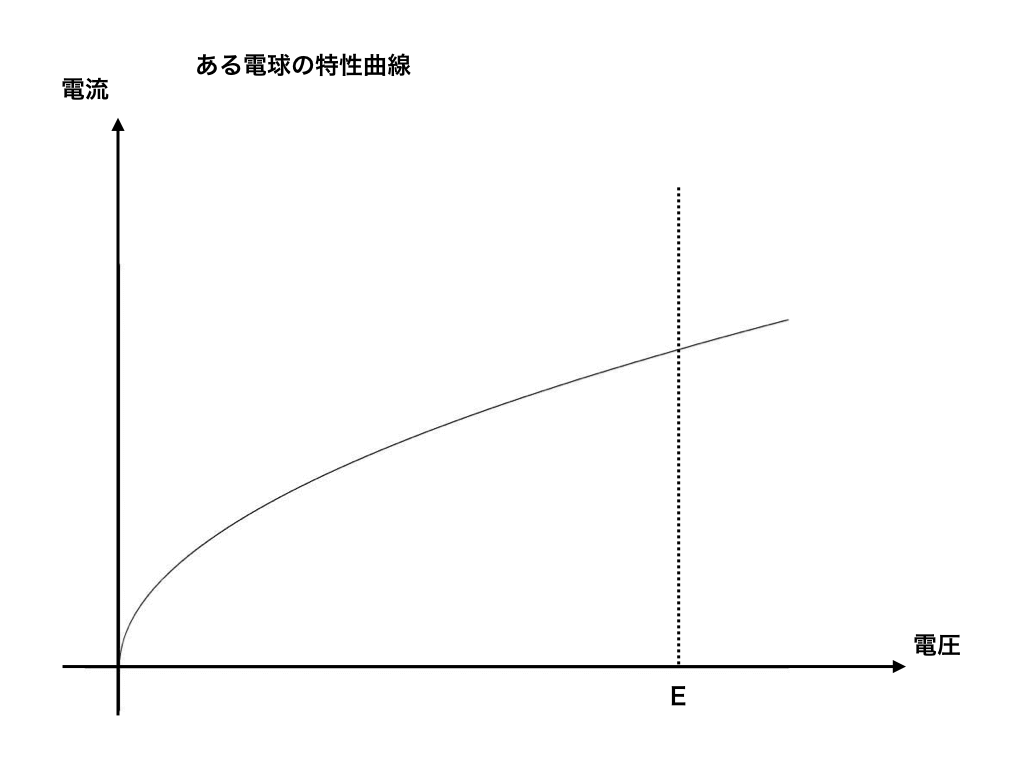
<電球の特性曲線(IーVグラフ)>
非オーム抵抗の問題でグラフの交点を求める理由とは
この種の問題では”I-Vグラフ上に与えられた曲線に直線を書き込んで、その交点が答えになる”という解法だけを覚えてしまっている人が少なくありません。
しかしこの解法を丸暗記する方法では、ちょっと問題を複雑にされると解けなくなるので、仕組みを理解した上で使わなければいけません。
さて、グラフに直線を書き込んで交点を求める理由は、非常に単純です。
例えば、数学で\(y=xとy=2x+2\)の解を求めるとき、普通は代入して(x,y)を求めると思います。
しかし別の解法として、次の図の様に2つの直線の式を書いた時にできる交点も同じく解になります。
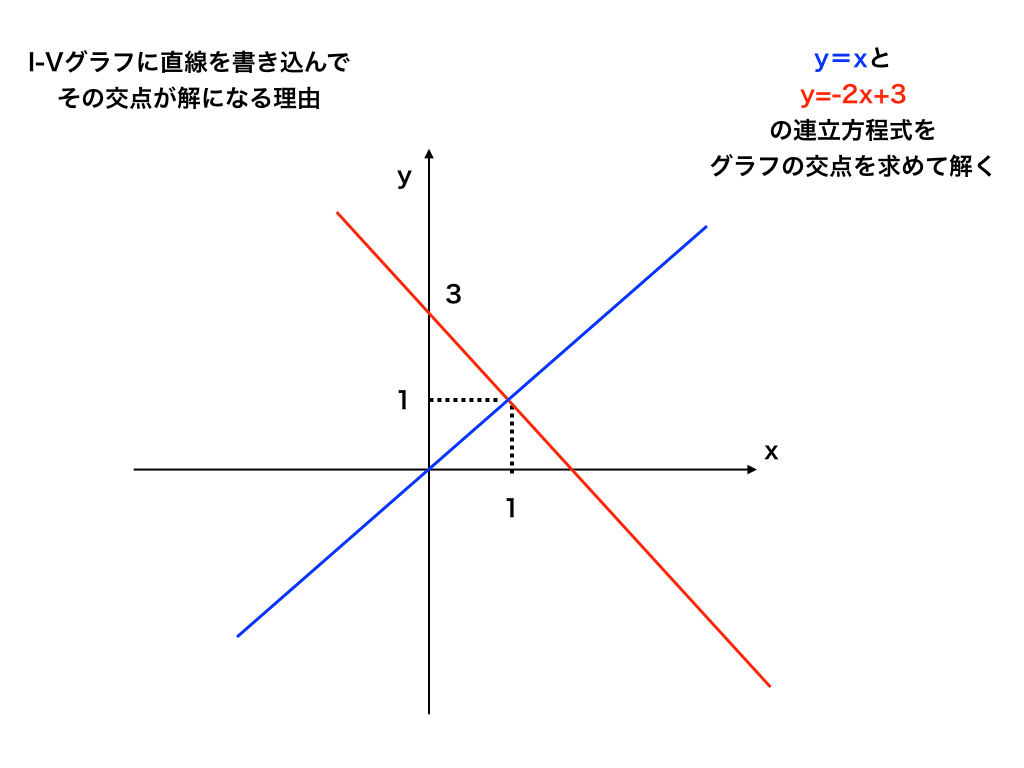
<例:連立方程式をグラフで解く>
I-Vグラフの交点を求める理由も上の場合と同じで、非オーム抵抗の曲線(特性曲線)の式が基本的には表せない(あるいは複雑になる)ので、
曲線の方程式との連立方程式を解く代わりとして、グラフの交点を求める方法を取っているのです。
非オーム抵抗の問題の解答
では、先ほどの非線形抵抗の問題の解答を載せておきます。
V,Iが求まる理屈さえ理解していれば、あとはグラフに直線を描き入れて交点の値を読み取ればOKです。
今、電球の電圧と電流(直流回路なので、この電流は抵抗にも同じだけ流れます)を求めたいので、これらをV’、I'とそれぞれ置いて、電池の電圧がE(V)より

$$E=RI'+V'(下の図の青線の式です)$$を特性曲線の上に書くことで
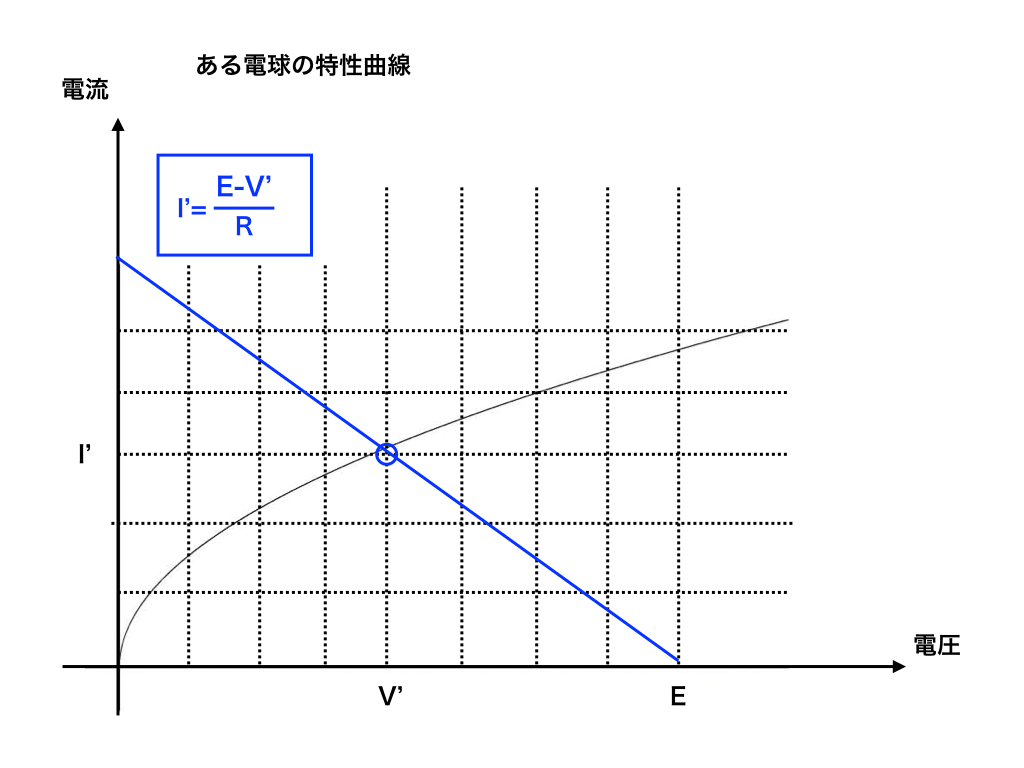
青丸で囲った部分の電圧、電流が例題の答えになります。
・具体的な数値を使った問題は教科書や参考書等に必ず載っているので、ぜひこの記事の内容を思い出しながら解いてみてください。
非オーム抵抗まとめと関連記事
・非オーム抵抗が線形にならない理由をイオンの熱運動や電子の振る舞いとともにイメージしておくこと
・特性曲線のグラフを使う解法を丸暗記するのではなく、仕組みを理解して使うこと
・次回は、キルヒホッフの法則〜コンデンサー回路の問題まで解説していきます。
電磁気の記事と次回「キルヒホッフの法則と回路問題」へ
〜電流と回路シリーズ〜
<第1回>「電流の意味とI=envSの式の導出法を解説」
第2回:今ココです
<第3回>「キルヒホッフの第一・第二法則とその利用法」
<第4回>「コンデンサーを回路に含む問題の解法」
<<電磁気分野の記事まとめ>>:
「高校物理・物理基礎の電磁気をわかりやすく!解説まとめページ」←左のページで電磁気についての記事を集めています。
今回も最後までご覧頂き、有難うございました。
「スマナビング!」では、読者の皆さんのご意見ご感想の募集をコメント欄で行なっています。
また、 いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に付いては、お問い合わせページからご連絡下さい。

